可证明安全量子随机扩展与无特征零差检测gydF4y2Ba

随机数生成器(rng)是当今使用的许多计算方法和数字解决方案的基本构建块，例如模拟、优化、密码学和赌博。理想情况下，RNG的输出应该是gydF4y2Ba统一的gydF4y2Ba和gydF4y2Ba不可预测的gydF4y2Ba。第一个属性要求所有输出都是等概率的，第二个属性规定，即使有关于设备的侧面信息，观察者也不能做出比随机猜测更好的结果。事实上，在处理安全通信、区块链和数字彩票等数字技术时，后一种属性尤其重要，因为隐私和信息安全至关重要。gydF4y2Ba

量子过程由于其内在的概率性质是随机性的极好来源。特别是，通过利用量子测量的不确定性，理论上可以设计出完全均匀且不可预测的量子随机数发生器(qrng)gydF4y2Ba^{1gydF4y2Ba，gydF4y2Ba2gydF4y2Ba，gydF4y2Ba3.gydF4y2Ba}。标准方法使用基于模型的方法，其中底层概率模型基于特定的可信量子测量过程。然而，虽然这种方法提供了一种直接的方法来量化可提取的随机性的数量，但它很容易产生实现偏差(对于一个具体的例子，我们请读者参考ref。gydF4y2Ba^4gydF4y2Ba)。特别是，由于意外的设备变化，模型可能无法捕捉实际的物理过程，可提取的随机性的数量可能被高估。至关重要的是，当该设备被用于加密时，可能会导致灾难性的结果。gydF4y2Ba

一种优雅的解决方案是考虑新形式的qrng，它基于对底层量子测量过程的最小假设提供可证明的随机性。这是通过利用纠缠系统上量子测量所建立的独特相关性而实现的。最好的例子是设备独立(DI) QRNGgydF4y2Ba^{1gydF4y2Ba，gydF4y2Ba5gydF4y2Ba，gydF4y2Ba6gydF4y2Ba，gydF4y2Ba7gydF4y2Ba，gydF4y2Ba8gydF4y2Ba，gydF4y2Ba9gydF4y2Ba}。然而，鉴于对非局部相关无孔洞观测的实验要求很高gydF4y2Ba^{5gydF4y2Ba，gydF4y2Ba7gydF4y2Ba，gydF4y2Ba10gydF4y2Ba}一般认为，这种DI qrng的第一个实际应用可能是随机信标gydF4y2Ba^{7gydF4y2Ba，gydF4y2Ba8gydF4y2Ba}。gydF4y2Ba

还有其他qrng对系统做出合理的假设，只需要设备的部分特征。与DI qrng相比，这些方案在实现复杂性和随机数生成率方面提供了系统性能的改进。由于部分特征，这类QRNG通常被称为半di QRNG。不同QRNG研究的比较见表gydF4y2Ba1gydF4y2Ba。gydF4y2Ba

对于实际的半di随机生成，在实际应用中非常需要以下特征。首先，随机生成的安全性应仅依赖于对系统运行及其关键组件的几个合理假设。这将确保这些qrng即使在出现意外的设备变化时也保持安全。其次，它还应该提供相对较高的随机性生成率。最后，QRNG应该具有成本效益和小足迹。后者在从手持设备到物联网的广泛应用中都是必不可少的。gydF4y2Ba

在这方面，平衡零差检测在实际随机生成中具有明显的优势。首先，由于平衡零差探测器只是由一对光电二极管和一些电子元件组成，它们很容易在集成光子平台上实现gydF4y2Ba^{11gydF4y2Ba，gydF4y2Ba12gydF4y2Ba，gydF4y2Ba13gydF4y2Ba，gydF4y2Ba14gydF4y2Ba}。因此，基于零差探测器的qrng在成本效益、紧凑性和系统稳定性方面具有独特的实际优势。其次，零差检测工作在室温下，无需额外冷却。这再次降低了系统的复杂性，并消除了对空间消耗的额外需求。gydF4y2Ba

不幸的是，由于许多实际的限制，真正的零差探测器经常偏离理想的正交测量-这是平衡零差探测的标准理论模型。首先，将零差探测器建模为输入光场的完美正交测量，需要本振子(LO)在高强度极限下工作gydF4y2Ba^{15gydF4y2Ba，gydF4y2Ba16gydF4y2Ba}，在实际实现中可能并非如此。此外，实现完美正交测量还需要完美光子数减法，这在有限共模抑制比(CMRR)和不平衡漂移的存在下是不平凡的。此外，与完美的正交测量相比，实用的零差探测器受到电子噪声、LO强度波动、有限的探测范围等的影响。虽然有关于如何解释模型中的这些缺陷的理论研究(例如，对电子噪声的标准理论处理是将其建模为独立的噪声gydF4y2Ba^{17gydF4y2Ba，gydF4y2Ba18gydF4y2Ba}具有高斯和平稳性质gydF4y2Ba^{18gydF4y2Ba，gydF4y2Ba19gydF4y2Ba})，该模型要求准确地描述每个缺陷。这项任务不仅在技术上要求很高，实际上，基于模型的方法存在错误精度的危险，因为零差探测器的质量可能会随着时间的推移而下降。在这种情况下，这将使模型失效，因此，零差检测产生的随机性可能被高估了。gydF4y2Ba

此外，还指出了实际零差探测器的有限带宽可能会导致连续几轮QRNG操作之间的相关性gydF4y2Ba^{19gydF4y2Ba，gydF4y2Ba20.gydF4y2Ba}。在这种情况下，实践中的实验弹不太可能表现出完全独立和同分布(i.i.d)的行为。特别是与量子态产生部分相比，具有shot-noise限制性能的零差探测器通常工作带宽更有限gydF4y2Ba^{17gydF4y2Ba，gydF4y2Ba21gydF4y2Ba}。因此，设计一种能够减轻(如果不能完全消除)系统操作的i.i.d.假设的随机性认证是非常有趣的。此外，由于任何QRNG协议都必须在有限的轮数内执行，因此应该考虑有限大小的影响(如统计波动)。这对于半DI和DI qrng尤其重要，它们的随机性证明依赖于实验统计，这必然会导致统计波动。gydF4y2Ba

在这项工作中，我们提出了一种新的基于零差检测的半di QRNG协议，并证明了其对量子侧信息的安全性。考虑到建模零差探测器的挑战，我们提出的框架将其视为一个黑盒量子测量，它避开了基于模型的方法的苛刻的特征要求。重要的是，我们的框架不需要测量设备上的任何i.i.d.假设，这可以保护协议的安全性，防止不同轮之间共享的潜在相关性。此外，所提出的协议是复合安全的gydF4y2Ba^{22gydF4y2Ba，gydF4y2Ba23gydF4y2Ba，gydF4y2Ba24gydF4y2Ba}，以确保我们的协议所产生的随机数可安全地用于密码应用。此外，我们表明，我们的协议可以产生更多的随机性比消费(为设备选择设置)在协议中。因此，我们的协议是gydF4y2Ba量子随机展开gydF4y2Ba(改革开放)协议。gydF4y2Ba

协议描述gydF4y2Ba

现在，我们将介绍我们提出的随机生成协议。我们所考虑的协议是一个准备-测量(P&M)协议，带有一个无特征的测量设备。为了说明该协议，可以方便地考虑一个由两部分组成的设备:一个可信的量子态源(我们假设由Alice操作)和一个无特征测量设备(由Bob操作)。因此，我们考虑的协议是一种自检协议，其中Bob的测量设备的工作不是先验的，而是可以在协议期间使用抽查方案进行验证，其中每一轮都随机分配为生成或测试轮。gydF4y2Ba

为此，假设在测试回合中，设备进行P&M游戏gydF4y2Ba\({{{{{{{\ mathcal {G }}}}}}}}\)gydF4y2Ba。在Bell非定域性的背景下，P&M游戏可以被认为是更著名的非本地游戏的P&M模拟gydF4y2Ba^{25gydF4y2Ba，gydF4y2Ba26gydF4y2Ba}和设备无关的协议。在P&M游戏中，Alice收到一个随机输入gydF4y2BaxgydF4y2Ba从一个预先定义的集合gydF4y2Ba\({{{{{{{\ mathcal {X }}}}}}}}\)gydF4y2Ba然后准备状态gydF4y2Ba\(左\ | {\ psi} _ {x} \ \纠正\)gydF4y2Ba从状态集合中gydF4y2Ba\({{{{{{{{\ mathcal{年代 }}}}}}}}}_{{{{{{{{\ mathcal {X }}}}}}}}}\)gydF4y2Ba。类似地，Bob接收一个输入gydF4y2BaygydF4y2Ba从一个预先定义的集合gydF4y2Ba\({{{{{{{\ mathcal {Y }}}}}}}}\)gydF4y2Ba并将其作为他的测量设置。让我们假设Alice和Bob以概率接收这些输入gydF4y2Ba问gydF4y2Ba（gydF4y2BaxgydF4y2Ba,gydF4y2BaygydF4y2Ba)，这是一个固定的游戏。对于每一对输入gydF4y2BaxgydF4y2Ba和gydF4y2BaygydF4y2Ba，游戏gydF4y2Ba\({{{{{{{\ mathcal {G }}}}}}}}\)gydF4y2Ba决定胜利的结果gydF4y2BabgydF4y2Ba_{xgydF4y2BaygydF4y2Ba}∈gydF4y2Ba{0,1}。对于给定的回合，当Bob输出获胜结果时，设备就赢得了比赛;否则，设备将输掉比赛。在方法部分，我们将介绍一个选择获胜结果的系统方法gydF4y2BabgydF4y2Ba_{xgydF4y2BaygydF4y2Ba}以及选择每对输入的概率gydF4y2Ba问gydF4y2Ba（gydF4y2BaxgydF4y2Ba,gydF4y2BaygydF4y2Ba)。gydF4y2Ba

我们提出的方案在方框中给出gydF4y2Ba1gydF4y2Ba

在本工作报告的实验中，我们考虑gydF4y2Ba\({{{{{{{\ mathcal {X }}}}}}}} =\{ \ \ 0, 1, 2, 3 \} \ \)gydF4y2Ba，即状态集gydF4y2Ba\({{{{{{{{\ mathcal{年代 }}}}}}}}}_{{{{{{{{\ mathcal {X }}}}}}}}} =\{\ 左| \α{e} ^ {ix \π/ 2}\ \纠正:x \ {{{{{{{\ mathcal {x }}}}}}}}\}\)gydF4y2Ba和gydF4y2Ba\({{{{{{{\mathcal{Y}}}}}}}} =\{0，\， 1\}\)gydF4y2Ba。此外，诚实实现对应零差检测，其LO的相位设置为gydF4y2BaφgydF4y2Ba=gydF4y2BaπgydF4y2Ba/ 2的时候gydF4y2BaygydF4y2Ba= 0和gydF4y2BaφgydF4y2Ba= 0时gydF4y2BaygydF4y2Ba= 1。测量装置将输出gydF4y2BabgydF4y2Ba零差测量结果为正，则= 0;否则，它会输出gydF4y2BabgydF4y2Ba= 1。在这种情况下，量子态对应于正交相移键控(QPSK)调制格式，它与标准光学调制技术兼容。值得注意的是，将协议推广到包括更多状态或更多测量设置，例如正交振幅调制(QAM)，是很简单的。gydF4y2Ba

安全框架gydF4y2Ba

现在我们来考虑一下协议的安全性。在这里，我们考虑一个框架，其中测量设备是无特征的，因此，在分析提议的协议的安全性时，我们将把Bob的测量作为一组抽象的测量算子。特别地，我们不假设Bob的测量装置对每一轮都表现出独立和相同的行为。gydF4y2Ba

同样，我们不假设量子信道忠实地传输爱丽丝发送的量子态，也不假设它在每一轮中都独立和相同地表现。由于我们不限制信道输出的希尔伯特空间的维度，我们可以用等距法对任何量子信道建模gydF4y2BaUgydF4y2Ba它保留了由爱丽丝的可信源准备的状态的内积。gydF4y2Ba

此外，我们还允许对手(或试图猜测协议输出的任何代理)Eve与Bob的未特征设备有一些预先共享的纠缠，但由于用于验证生成的随机性的方法的一些技术性问题，我们假设Eve在执行协议时不会获得额外的量子侧信息。对于QRNG协议中Alice和Bob都在同一个安全位置中的设置，可以很好地证明这个假设是正确的。gydF4y2Ba

最后，我们还假设该设备配备了可信和私有的随机种子，用于为每一轮选择输入以及执行种子提取。关于我们在随机性认证中所做假设的详细讨论，请读者参阅“方法”部分“随机性认证”。gydF4y2Ba

我们的协议的安全性依赖于量子证明强种子提取器，该提取器保证无论何时协议不中止，输出字符串都接近于理想的随机位串，该位串均匀随机，独立于对手持有的任何预先共享的量子信息以及初始随机种子。因此，在应用随机性提取之前，我们必须证明我们的协议产生了足够的随机性(根据原始字符串的条件平滑最小熵来衡量)。为此，我们采用熵累积定理(EAT)的框架。gydF4y2Ba^{27gydF4y2Ba，gydF4y2Ba28gydF4y2Ba，gydF4y2Ba29gydF4y2Ba，gydF4y2Ba30.gydF4y2Ba}。非正式地说，EAT指出，当我们的协议没有中止时，给定Eve的侧信息和随机输入的原始字符串的条件平滑最小熵至少为gydF4y2Ba

重要的是，前面的一项与回合数成线性比例gydF4y2BangydF4y2Ba可以通过分析单轮协议进行评估。比例常数gydF4y2BahgydF4y2Ba（gydF4y2BaωgydF4y2Ba,gydF4y2BaδgydF4y2Ba)，以及修正期限gydF4y2Ba\({{{{{{{\ mathcal {O }}}}}}}}(\ √6 {n}) \)gydF4y2Ba可以使用参考文献中介绍的半定义编程(SDP)技术进行计算。gydF4y2Ba^31gydF4y2Ba。更准确地说，我们有以下定理。gydF4y2Ba

定理1gydF4y2Ba

熵累积定理(由参考文献引理III.3修改而成。gydF4y2Ba^30.gydF4y2Ba))让Ω表示QRNG协议未终止的事件和gydF4y2BaρgydF4y2Ba^ΩgydF4y2Ba最终状态以这个为条件。让gydF4y2BafgydF4y2Ba(1−gydF4y2BaνgydF4y2Ba)是单轮条件冯·诺依曼熵的仿射下界gydF4y2Ba\({{{{{{{\ mathcal {G }}}}}}}}\)gydF4y2Ba的概率gydF4y2BaνgydF4y2Ba。对于固定参数gydF4y2BaϵgydF4y2Ba_{年代gydF4y2Ba},gydF4y2BaϵgydF4y2Ba_EAgydF4y2Ba,gydF4y2BaβgydF4y2Ba∈gydF4y2Ba(0,1)，那么要么我们的QRNG协议以大于1−的概率中止gydF4y2BaϵgydF4y2Ba_EAgydF4y2Ba或gydF4y2Ba

函数的显式表达式gydF4y2BafgydF4y2Ba,gydF4y2BaVgydF4y2Ba,gydF4y2BaKgydF4y2Ba可以在“方法”一节“随机性认证”中找到。gydF4y2Ba

定理1对任意选择都成立gydF4y2BaβgydF4y2Ba，就像我们在Methods部分看到的那样，我们可以选择gydF4y2Ba\(\beta \propto 1/\√{n}\)gydF4y2Ba这样，修正期限将与gydF4y2Ba\ \√{n} \)gydF4y2Ba如前所述。我们引用参数gydF4y2BaϵgydF4y2Ba_EAgydF4y2Ba即熵累积误差。从定理1中可以看出，它量化了我们对遇到一个事件的容忍度，在该事件中，协议没有中止，但下限(gydF4y2Ba2gydF4y2Ba)对累积熵的假设不成立。gydF4y2Ba

最后，随着条件光滑最小熵的下界的建立，我们可以使用量子剩余哈希引理gydF4y2Ba^{32gydF4y2Ba，gydF4y2Ba33gydF4y2Ba}查找输出字符串的可提取长度gydF4y2BaZgydF4y2Ba，表示为gydF4y2BaℓgydF4y2Ba。作为提取程序种子gydF4y2Ba年代gydF4y2Ba是否是协议输出的一部分gydF4y2BaKgydF4y2Ba，期望的净随机扩展率gydF4y2BargydF4y2Ba_网gydF4y2Ba然后定义为gydF4y2Ba

在哪里gydF4y2BaℓgydF4y2Ba_在gydF4y2Ba是在选择设备设置的协议期间使用的预期随机量。gydF4y2Ba

随机认证的细节，输入随机性的估计分别在“方法”的“随机认证”和“输入随机性”部分。gydF4y2Ba

实验实现gydF4y2Ba

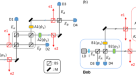
为了验证所提方案的可行性，我们搭建了光纤实验系统。原理图如图所示。gydF4y2Ba1gydF4y2Ba一个。gydF4y2Ba

实验系统由量子态生成和量子态测量两部分组成。在量子态产生过程中，激光二极管发射中心波长为1550 nm、线宽为50 kHz的连续波激光，激光分为两条路径，一条用于量子态制备，另一条作为本振子(LO)用于零差检测。在信号路径中，一个强度调制器(IM)首先将c.w.激光弯曲成每个脉冲宽度为4 ns的脉冲，用于定义量子态的时间模式。此外，IM还可以对QAM-16状态的产生进行强度调制。相位调制器(PM)调制量子态的相位。然后利用光衰减器将光信号衰减到单光子能级，最终生成QPSK量子态gydF4y2Ba\(\{\左|\alpha {e}^{ix\pi /2}\右rangle \}\)gydF4y2Ba在哪里gydF4y2BaxgydF4y2Ba∈gydF4y2Ba{0,1,2,3}，其星座图如图所示。gydF4y2Ba1gydF4y2Bab。gydF4y2Ba

在量子态测量中，采用了零差探测器。为了最大化产生的随机性，我们开发了一种高效、低噪声的光纤耦合零差检测器。为了尽量减少光学损耗，我们首先采用一对高效率光电二极管(PDs)进行光子探测。此外，我们还采用了增透涂层渐变折射率(GRIN)透镜实现光纤与pd的光耦合。包括耦合损失在内的PD的总体效率分别为98.3%和98.8%。在检测之前，信号和LO被平衡偏振维持光纤分束器(BS)干扰，为稳定有效的干扰提供良好的模式匹配。经过两个臂的小心平衡，光电流被减去，然后由一个低噪声放大器放大。我们的零差检测器的表征结果如图所示。gydF4y2Ba1gydF4y2Ba(d, e).我们的零差探测器的3db带宽为~72 MHz，间隙(射击噪声与电子噪声之比)测量为16.94 dB, LO为10 mW。综合考虑所有因素，我们的零差探测器的总有效效率达到91.7%。零差表征和建模的细节在“方法”部分“零差检测器建模和表征”中提供。gydF4y2Ba

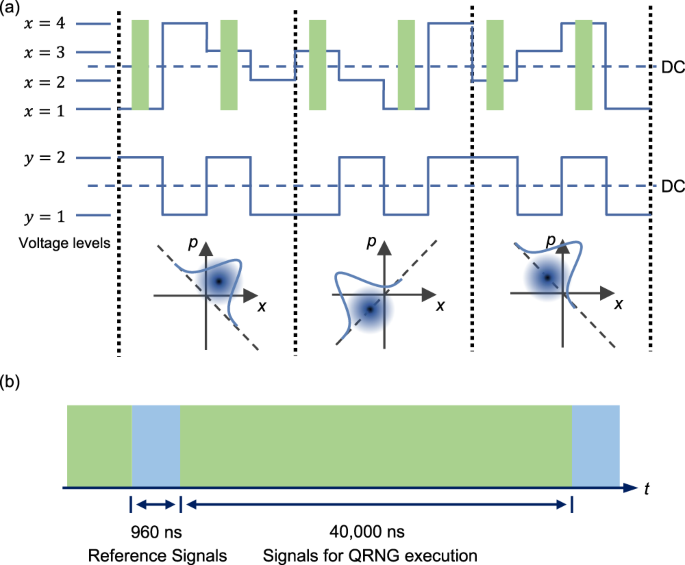
在实际实验中，量子态制备和测量的设置需要优化以获得较高的净随机膨胀率。例如，在大多数情况下可以选择随机生成回合(测试概率较小)gydF4y2BaγgydF4y2Ba)得到最优生成速率。这对我们的交流耦合系统提出了一个问题，例如零差检测器和用于驱动调制器的放大器，其中首选dc平衡数据流以消除潜在的信号失真gydF4y2Ba^34gydF4y2Ba。为了缓解这一问题，我们在实验中应用了互补调制方案，其中基于QPSK调制的协议被执行，如图所示。gydF4y2Ba2gydF4y2Baa.在我们的方案中，量子态的制备是在基于两个连续的时间模式的双模相干态上进行的。在这种情况下，调制模式的状态准备和LO相位设置自然是dc平衡与任何设置gydF4y2BaxgydF4y2Ba和gydF4y2BaygydF4y2Ba。此外，两种时间模式是由a调制gydF4y2BaπgydF4y2Ba相位差，而LO相位设置保持不变。因此，两种时间模式的个别正交测量的期望值具有相反的值。因此，零差检测器的输出对于所有实验设置也是自然的dc平衡。在这种情况下，双模相干态的正交测量gydF4y2Ba\ ({q} _ {t} = \压裂{1}{\ sqrt {2}} ({q} _ {e} - {q} _ {l}) \)gydF4y2Ba,在那里gydF4y2Ba问gydF4y2Ba_egydF4y2Ba和gydF4y2Ba问gydF4y2Ba_lgydF4y2Ba为两个单独的时间模式的正交测量值。有关双模相干态的详细信息，请参见“方法”一节“双模相干态”。gydF4y2Ba

为了忠实地实现QRNG协议，信号和LO之间需要一个固定的相位参考。为此，一个锁相的反馈控制(图中未显示)。gydF4y2Ba1gydF4y2Baa)通过分析参考信号和QRNG执行信号的统计数据来部署。我们的QRNG的时间框架配置说明如图所示。gydF4y2Ba2gydF4y2Bab。gydF4y2Ba

在这一点上，我们强调，由于我们的QRNG协议不需要测量设备(即零差检测器)的任何特性，我们在损耗和噪声降低、锁相等方面的努力不会影响gydF4y2Ba稳健gydF4y2Ba的随机性认证，但肯定会提高性能方面的随机性产生率，系统的稳定性(这是有关的gydF4y2Ba完整性gydF4y2Ba协议)，等等。gydF4y2Ba

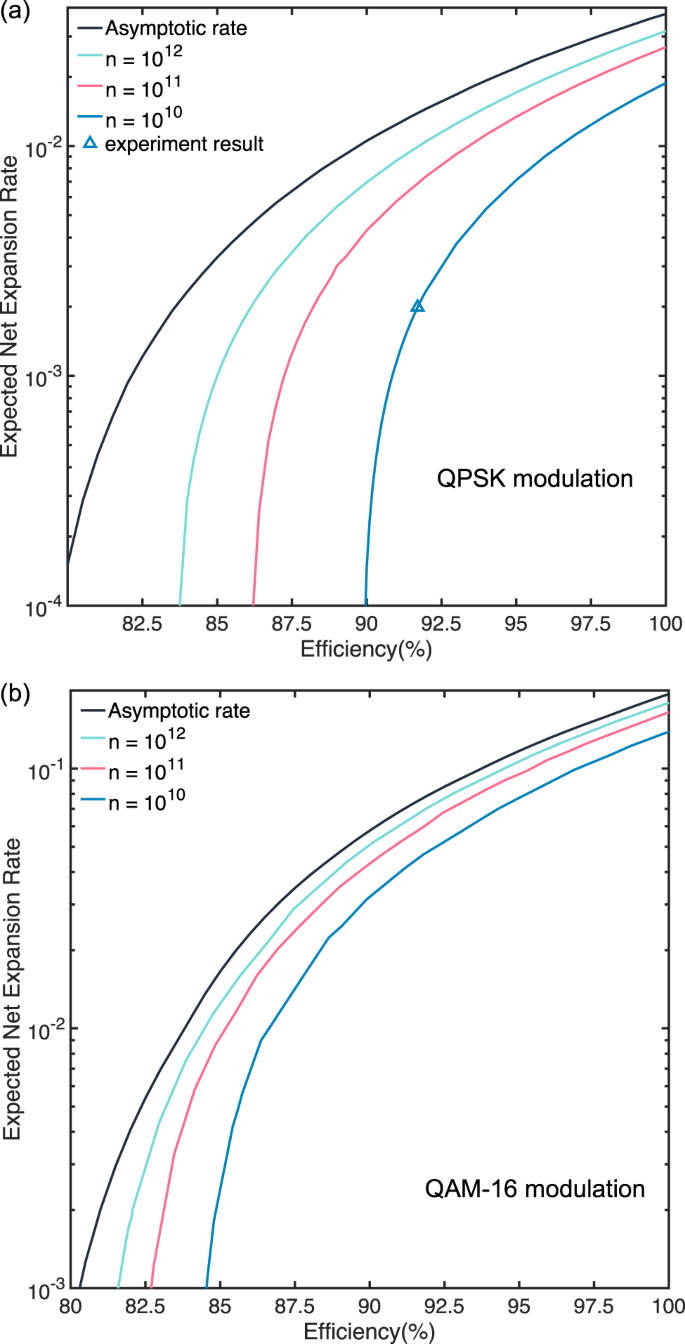
基于定理1，量子剩余哈希引理，以及Eq.(所给出的期望净随机展开率的定义。gydF4y2Ba3.gydF4y2Ba)，我们首先模拟我们所提出的协议的性能。QPSK调制和QAM-16调制模拟的净随机膨胀率如图所示。gydF4y2Ba3.gydF4y2Ba分别是A和b。gydF4y2Ba

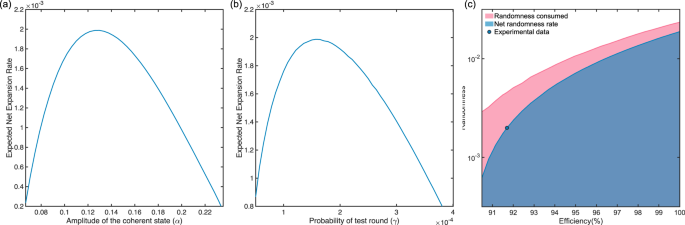
实验中使用的参数如表所示。gydF4y2Ba2gydF4y2Ba，其中为平均光子数gydF4y2Ba∣gydF4y2BaαgydF4y2Ba∣gydF4y2Ba^2gydF4y2BaQPSK格式的量子态，即选择测试回合的概率gydF4y2BaγgydF4y2Ba根据我们设置的系统效率和所选的安全参数进行优化，如图所示。gydF4y2Ba4gydF4y2Baa, b.期望的净随机性扩展率与消耗的随机性的关系如图所示。gydF4y2Ba4gydF4y2Bac。gydF4y2Ba

根据“方法”部分“制定P&M游戏”中描述的结构。，我们制定了P&M博弈gydF4y2Ba\({{{{{{{\ mathcal {G }}}}}}}}\)gydF4y2Ba用于我们的QRNG协议，如表所示。gydF4y2Ba3.gydF4y2Ba，它决定了Alice输入选择设置的概率gydF4y2BaxgydF4y2Ba和Bob的输入gydF4y2BaygydF4y2Ba测试回合和评分规则。基于我们的诚实实现模型(详见“方法”一节“双模相干态”)，我们设置gydF4y2BaωgydF4y2Ba= 0.59422和gydF4y2BaδgydF4y2Ba= 0.00189，分别表示期望获胜概率和获胜概率的置信区间。gydF4y2Ba

我们收集gydF4y2BangydF4y2Ba= 1 × 10gydF4y2Ba^10gydF4y2Ba在实验中进行了多轮数据分析，并得到了观测到的获胜概率gydF4y2BaωgydF4y2Ba_{奥林匹克广播服务公司gydF4y2Ba}= 0.59443，与期望值非常接近。玩家输掉比赛的回合数是942820，在可接受范围内gydF4y2BangydF4y2Ba_{失去了gydF4y2Ba}≤946026。因此，协议执行被接受，我们可以证明通过运行协议可以获得每轮至少0.00455比特的总随机性生成率(协议每轮产生的随机性)。考虑到为确定给定一轮是否是测试轮而投入的随机性，以及Alice和Bob的输入(gydF4y2BaxgydF4y2Ba和gydF4y2BaygydF4y2Ba)，在我们的例子中，预期的随机性消耗率是每轮0.00256比特。因此，我们系统的期望净随机扩展率为0.00199比特/轮。试验轮的观测实验结果见表gydF4y2Ba4gydF4y2Ba。gydF4y2Ba

最后，我们在随机种子的帮助下使用Toeplitz哈希实现随机抽取。Toeplitz哈希是一个双通用哈希函数家族，它已被证明是一个强大的随机性提取器gydF4y2Ba^{32gydF4y2Ba，gydF4y2Ba35gydF4y2Ba，gydF4y2Ba36gydF4y2Ba}。这意味着Toeplitz哈希不仅从弱熵源中提取随机性，而且还保证输出字符串独立于种子。因此，在这项工作中，随机提取所需的种子不被认为是消耗的随机性，因为由于强提取器的特性，种子可以连接到输出。gydF4y2Ba

我们使用Zynq Ultrascale+ FPGA (XCZU28DR)来实现随机抽取。我们构造一个大小为45 × 10000的Toeplitz矩阵，从原始数据中提取随机数。为了获得更快的提取速度，我们在提取过程中将Toeplitz矩阵进一步分割为大小为45 × 1000的子块。总的来说，原始数据的大小为10.622 Gbits(我们保守地收集了比1 × 10多一点的数据gydF4y2Ba^10gydF4y2Ba)，我们从中提取了47.8 Mbits的随机数。Toeplitz哈希在FPGA上的详细实现在“随机提取”一节中提供。gydF4y2Ba

讨论gydF4y2Ba

在本节中，我们将讨论我们工作的优势和局限性。除了由于其对检测侧信道的免疫而具有很高的安全性之外，我们协议的主要优势之一是其小型化的潜力。下面，我们将讨论在硅光子集成电路(PIC)上实现的拟议协议的可行性，PIC是集成光子应用的领先平台，在小型化、与CMOS微电子器件的兼容性和高速信号处理方面具有显著优势。来自主要代工厂的工艺设计套件(pdk)可以在单个芯片上提供关键组件，具有良好的性能稳定性，适合批量生产gydF4y2Ba^{37gydF4y2Ba，gydF4y2Ba38gydF4y2Ba，gydF4y2Ba39gydF4y2Ba}。gydF4y2Ba

通过利用成熟的绝缘体上硅(SOI)技术，在硅PIC上的光波导能够提供低传输损耗和大集成密度。2 × 2分束器可采用倏逝耦合器或多模干涉耦合器实现。gydF4y2Ba

对于高速光调制，载波损耗型调制器可用于量子态的制备。高速锗光电探测器可用于光学量子态的零差探测。gydF4y2Ba

集成激光器是我们QRNG系统的关键组件，它是阻碍在单个硅芯片上实现完整系统集成的一个障碍。这是因为纯晶体硅缺乏直接带隙，排除了单片硅激光器的可能性gydF4y2Ba^38gydF4y2Ba。幸运的是，最近基于封装或异构集成技术的集成激光技术可以解决这一问题gydF4y2Ba^37gydF4y2Ba。gydF4y2Ba

在这方面，我们的主要目标之一是通过实验验证所提出的协议的关键概念，这最终归结为实现测量设备的足够有效效率，以证明正的净随机性扩展率。为此，我们需要在硅pic上的高效pd。幸运的是，这种高效的pd在目前的技术范围内。例如，Globalfoundries在1310 nm波长提供>1 A/W响应的pd，对应于>94%的量子效率gydF4y2Ba^40gydF4y2BaAIM Photonics在1550 nm波长提供的量子效率为>80%gydF4y2Ba^41gydF4y2Ba。此外，如果可以使用定制组件，则可以更灵活地提高效率。因此，我们的QRNG协议的完全集成版本实际上可以通过现有的PIC技术实现。gydF4y2Ba

然而，在系统层面上，我们目前工作的主要局限性是相对较低的随机性生成/扩展率。我们现在讨论随机展开率有限的一些原因。其中一个原因是我们在应用EAT时使用Eve的猜测概率来构造最小权衡函数。虽然使用SDP松弛可以很容易地计算猜测概率，但这种结构通常不严密。最近，条件冯·诺依曼熵的一个紧密边界也与我们的SDP松弛相容gydF4y2Ba^42gydF4y2Ba。通过在条件冯·诺依曼熵上加入新的边界，看看是否可以获得随机展开率的改进，这将是很有趣的。gydF4y2Ba

随机扩展率有限的另一个原因是我们将零差检测输出粗粒度化。实际上，这里我们考虑了一个测量设备，它给出二进制输出;而在实际中，零差测量实际上有大量由ADC电路决定的离散箱。粗粒度化是为了简化协议，因为它允许我们在参数估计步骤中简单地监视获胜概率。然而，我们的安全分析可以扩展到使用ref框架考虑更多的输出。gydF4y2Ba^30.gydF4y2Ba。然而，在协议中使用的输出数量和随机性生成率之间存在权衡，因为随着获得每个bin的概率变得越来越小，对输出进行细粒度处理将增强统计波动的影响。为测量输出找到最佳的箱子数量值得在未来进行更深入的研究。gydF4y2Ba

其次，我们的协议还要求较高的检测效率来生成网络随机性展开。由于电子噪声(及其等效效率损失)与系统的工作带宽之间存在权衡，我们实验中的工作频率相对较低，这导致了较低的随机性产生率。高检测效率要求的原因之一是协议中使用的状态的选择。在我们的实验中，为了实验的简单性，我们使用QPSK编码。然而，这种状态的选择可能不是最优的。如图所示。gydF4y2Ba3.gydF4y2Bab，选择QAM-16星座可以明显提高每脉冲的随机性展开，降低所需的探测效率。这将导致实际随机扩展率的显著增加。gydF4y2Ba

最后，在这项工作中，我们假设设备与环境充分隔离，以便在协议开始之前获得对手可访问的任何量子侧信息。虽然这一假设对于qrng来说是合理的，因为双方都在同一个安全位置，但它仍然可以使用最近开发的EAT泛化来消除gydF4y2Ba^{43gydF4y2Ba，gydF4y2Ba44gydF4y2Ba}。这种宽松的假设可能适用于更悲观的情况，即设备被不安全的环境包围，任何分散在通道中的光子都可能落入对手手中。由于广义EAT中的边界与在原始熵积累框架下导出的边界相似(修正项略有不同)，我们预计在更悲观的情况下，我们的QRNG仍然可以表现出随机性扩展。我们把这个调查留到以后的工作。gydF4y2Ba

总之，我们提出了一个基于完全无特征零差检测器的QRNG协议。安全分析考虑了有限尺寸效应和非i.i.d。测量过程，提供随机数生成，即证明存在量子侧信息。为了验证该方案的可行性，我们搭建了一个高效、低噪声的光纤耦合零差检测器进行实验。在1550 nm处，光电二极管对的平均量子效率为98.55%，在10 mW LO输入时，测得的间隙为16.94 dB。零差检测器的有效效率为91.7%。为了正确实现我们的协议并消除潜在的信号失真，我们提出了一种互补调制方案，并采用双模相干态进行量子态制备。对于QRNG协议执行期间的任何实验设置，这保证了调制信号和测量结果都是dc平衡的数据流。系统在2.5 MHz的重复频率下工作，最终得到总随机生成率为0.00455，净随机扩展率为0.00199，随机扩展率为1 × 10gydF4y2Ba^10gydF4y2Ba协议执行轮。此外，我们还证明了我们的协议与硅光子学平台兼容，并且易于在硅PIC上实现。gydF4y2Ba

总之，我们的结果展示了一个具有自检功能和可证明安全性的实用QRNG，显示出为实际和私人使用提供可证明随机性的巨大潜力。gydF4y2Ba

随机性认证gydF4y2Ba

在解释协议的随机性认证之前，我们首先解释协议的安全标准。考虑一个产生输出字符串的随机生成协议，我们将其标记为gydF4y2BaZgydF4y2Ba。在像我们这样的自检协议中，合法的各方在协议期间交换一些经典信息是很常见的(例如，在参数估计步骤中)。我们用“”来表示协议中任何经典通信的文本gydF4y2Ba米gydF4y2Ba。再假设该协议涉及到随机抽取。我们将表示用于随机抽取的种子gydF4y2Ba年代gydF4y2Ba。最后，Eve可以获得的任何侧面信息将被表示为gydF4y2BaEgydF4y2Ba。对于给定的协议运行，让我们假设它的输出可以用量子态来描述gydF4y2Ba

在这里，我们解释了协议可能中止的概率(在这种情况下，我们用gydF4y2Ba\ \ varnothing \ ()gydF4y2Ba)。此外,gydF4y2BaτgydF4y2Ba_lgydF4y2Ba表示具有长度的均匀随机字符串gydF4y2BalgydF4y2Ba用下标和表示gydF4y2Ba\({\波浪号{\ρ }}_{{{{{{{{\ 男朋友{M}}}}}}}} E} ^ {\ varnothing} \)gydF4y2Ba描述了伊芙的侧信息和协议中止时的经典文本的亚正常化状态。另一方面，亚正常化状态gydF4y2Ba\({\波浪号{\σ }}_{{{{{{{{\ 男朋友{Z }}}}}}}}{{{{{{{\ 男朋友{年代 }}}}}}}}{{{{{{{\ 男朋友{M}}}}}}}}} \ E)gydF4y2Ba第二项描述协议未终止时的状态gydF4y2Ba

所有可能的输出和种子字符串的总和，我们用gydF4y2BazgydF4y2Ba和gydF4y2Ba年代gydF4y2Ba。亚正常化状态gydF4y2Ba\({\波浪号{\ρ }}_{{{{{{{{\ 男朋友{M}}}}}}}} E} ^ {z \ s} \)gydF4y2Ba描述伊芙的侧面信息和经典文本的状态是否以输出字符串为条件gydF4y2BazgydF4y2Ba种子线是gydF4y2Ba年代gydF4y2Ba。表示协议没有被Ω中止的事件，我们有gydF4y2Ba

将协议未中止的状态归一化，我们得到gydF4y2Ba\({\σ }_{{{{{{{{\ 男朋友{Z }}}}}}}}{{{{{{{\ 男朋友{年代 }}}}}}}}{{{{{{{\ 男朋友{M}}}}}}}}}: ={\波浪号{\σ }}_{{{{{{{{\ 男朋友{Z }}}}}}}}{{{{{{{\ 男朋友{年代 }}}}}}}}{{{{{{{\ 男朋友{M}}}}}}}}} / E公关[ω\]\ \)gydF4y2Ba。我们说QRNG是gydF4y2BaεgydF4y2Ba_苏gydF4y2Ba声音如果gydF4y2Ba

对于固定的gydF4y2BaεgydF4y2Ba_苏gydF4y2Ba∈gydF4y2Ba(0, 1)。在这里,gydF4y2Ba\({\σ }_{{{{{{{{\ 男朋友{M}}}}}}}} E } ={{{{{{{{\ rm {Tr }}}}}}}}}_{{{{{{{{\ 男朋友{Z }}}}}}}}{{{{{{{\ 男朋友{年代 }}}}}}}}}[{\ σ }_{{{{{{{{\ 男朋友{Z }}}}}}}}{{{{{{{\ 男朋友{年代 }}}}}}}}{{{{{{{\ 男朋友{M}}}}}}}} E}] \)gydF4y2Ba。非正式地说，协议的可靠性意味着要么协议以高概率中止，要么协议的输出将接近(在跟踪距离中)一个具有长度的随机字符串gydF4y2BaℓgydF4y2Ba这与种子无关gydF4y2Ba年代gydF4y2Ba，协议中交换的任何经典信息gydF4y2Ba米gydF4y2Ba，以及伊芙的侧面信息gydF4y2BaEgydF4y2Ba。重要的是，上面的安全性定义是可组合的。因此，该协议的输出可以安全地用于其他加密应用程序。gydF4y2Ba

然而，总是中止的协议可以满足式中给出的稳健性条件(gydF4y2Ba7gydF4y2Ba)，这样的协议显然是不可取的。因此，我们还提出了一个额外的要求，即当设备按预期工作时，协议将成功地产生大概率的随机字符串。在形式上，我们称之为协议gydF4y2BaεgydF4y2Ba_comgydF4y2Ba-如果它的真实实现(可能使用不完美的设备)满足以下要求，则为完整gydF4y2Ba

对于一些固定的gydF4y2BaεgydF4y2Ba_comgydF4y2Ba∈gydF4y2Ba(0, 1)。注意下标“honest”强调Pr[Ω]gydF4y2Ba_{诚实的gydF4y2Ba}是在假设装置按预期工作的情况下计算的，特别是在每一轮中独立和相同。在这种情况下，我们通常会对设备的行为进行建模，包括其不完善性，并计算在这种情况下协议中止的概率(例如，由于参数估计的统计波动)。gydF4y2Ba

接下来，为了分析协议的安全性，我们假设如下:gydF4y2Ba

1. 1.gydF4y2Ba

   量子理论是正确的。gydF4y2Ba

2. 2.gydF4y2Ba

   Alice有一个可信的量子态源，可以准确地准备协议指定的代码状态。gydF4y2Ba

3. 3.gydF4y2Ba

   该设备配备了可信和私有的随机种子。gydF4y2Ba

4. 4.gydF4y2Ba

   设备可以访问可信的经典设备来执行任何经典的后处理。gydF4y2Ba

5. 5.gydF4y2Ba

   该设备被很好地隔离，因此它不会泄漏额外的量子侧信息或输出字符串。gydF4y2Ba

现在，我们将简要阐述上述假设。第一个假设通常被认为是理所当然的，因为量子理论是我们目前在小范围内对自然最好的描述。因此，在本文中，我们将假设Eve和协议中使用的设备遵守量子物理定律。gydF4y2Ba

第二种假设实际上可以通过对爱丽丝来源的仔细描述得到证明。由于与QRNG相关的场景考虑了Alice和Bob彼此靠近的情况，因此可以合理地认为源受到了很好的保护，不受其他量子加密协议中可能出现的源侧通道攻击(例如，QKD中的特洛伊木马攻击)的影响gydF4y2Ba^45gydF4y2Ba)。特别地，我们假设源在每一轮中表现相同且独立。gydF4y2Ba

第三个假设是必要的，因为在这个协议中产生原始随机字符串的测量设备是无特征的。如果输入不是从可信的随机数发生器中选择的，一种可能的情况是，在协议运行之前，未特征的测量设备可以访问输入。在这种情况下，重现协议的真实实现所获得的统计信息是微不足道的。此外，由于我们的随机性认证将使用EAT，使用可信随机数生成器可以强制量子马尔可夫链条件。最后，协议的最后一步使用种子提取，这需要一个私有的和均匀随机的种子。gydF4y2Ba

第四个假设对于任何QRNG协议都是必要的，以防止安全标准被破坏。例如，当随机抽取没有正确执行时，很明显，稳健性准则可能不满足。此外，当输出字符串泄漏时，猜测QRNG的输出是微不足道的。gydF4y2Ba

最后一个假设是必要的，有两个原因。首先，当设备泄漏输出字符串时，协议的安全性显然为null。其次，由于EAT的一些技术性问题，我们需要假设Eve可用的量子侧信息在协议运行时没有更新。值得注意的是，这个假设对于qrng来说并没有太大的限制，因为Alice和Bob都在同一个安全位置内。最近，有一个通用版本的EATgydF4y2Ba^{43gydF4y2Ba，gydF4y2Ba44gydF4y2Ba}允许伊芙的量子侧信息随着协议的运行而更新，因此，看看设备不会泄露额外量子侧信息的假设是否可以放松，这将是很有趣的。gydF4y2Ba

在提到了我们在安全分析中需要的假设之后，我们再次强调，我们没有对测量设备和量子通道做任何假设。特别是，在给定的一轮中，这些组件的行为可以与它们在前几轮中的输入和输出有任意的相关性(不像我们假设在每一轮中表现独立和相同的源)。值得注意的是，我们的协议仍然是安全的，即使零差探测器有退化，或者当伊芙与鲍勃的无特征测量设备有一些预先共享的纠缠。gydF4y2Ba

如前所述，我们希望协议同时满足完整性和稳健性标准。我们首先证明了我们的QRNG协议的完整性。为此，我们使用下面的定理。gydF4y2Ba

定理2gydF4y2Ba

(二项累积分布的边界gydF4y2Ba^{46gydF4y2Ba，gydF4y2Ba47gydF4y2Ba})让gydF4y2Ba在{\ \ (n \ mathbb {n}} \)gydF4y2Ba，gydF4y2BapgydF4y2Ba∈gydF4y2Ba(0,1)， letgydF4y2BaXgydF4y2Ba是根据分布的随机变量gydF4y2BaXgydF4y2Ba~二项(gydF4y2BangydF4y2Ba,gydF4y2BapgydF4y2Ba)。然后，对于任何整数gydF4y2BakgydF4y2Ba这样0≤gydF4y2BakgydF4y2BangydF4y2Ba，我们有gydF4y2Ba

在哪里gydF4y2Ba

因为如果gydF4y2Ba\(左| \ \ {{C} _{我}:{C} _{我}= 0 \}\ | \,> \ n \γ(1 - \ω+δ)\ \)gydF4y2Ba，我们可以应用定理2，与在ref中相同的方式。gydF4y2Ba^9gydF4y2Ba，得到协议被终止概率的上限值gydF4y2Ba

因此，通过选择完整性误差为gydF4y2Ba

我们的QRNG协议满足完备性条件。gydF4y2Ba

接下来，为了证明我们的QRNG协议的稳健性，我们将使用以下量子剩余哈希引理(参考文献的定理8)。gydF4y2Ba^33gydF4y2Ba)。gydF4y2Ba

定理3gydF4y2Ba

(量子剩余哈希引理gydF4y2Ba^33gydF4y2Ba)让gydF4y2Ba\({\rho}_{{{{{{{{\bf{B}}}}}}}}{E}^{{\prime}}}\)gydF4y2Ba是经典量子态gydF4y2Ba\({{{{{{{\ mathcal {F }}}}}}}} =\{{ f} _ {}: {\ {1 0 \ \}} ^ {n} \{\{1 0 \ \}} ^{\魔法}\}\)gydF4y2Ba是一个双通用哈希族gydF4y2BaZgydF4y2Ba=gydF4y2BafgydF4y2Ba_{年代gydF4y2Ba}（gydF4y2BaBgydF4y2Ba)和种子gydF4y2Ba年代gydF4y2Ba∈gydF4y2Ba{0,1}gydF4y2Ba^米gydF4y2Ba是统一选择的。令0 κgydF4y2Ba≤gydF4y2BaεgydF4y2Ba/2 < 1，我们有gydF4y2Ba

在哪里gydF4y2BaτgydF4y2Ba_ℓgydF4y2Ba和gydF4y2BaτgydF4y2Ba_米gydF4y2Ba这些字符串的长度是均匀随机的吗gydF4y2BaℓgydF4y2Ba和gydF4y2Ba米gydF4y2Ba分别。因此，如果我们选择输出长度为gydF4y2Ba

最大化在哪里被取代gydF4y2BaκgydF4y2Ba∈gydF4y2Ba(0,gydF4y2BaεgydF4y2Ba，那么，我们有gydF4y2Ba

另一方面，对于一个固定的平滑参数gydF4y2BaϵgydF4y2Ba_{年代gydF4y2Ba}， EAT(定理1)保证协议终止的概率至少为1−gydF4y2BaϵgydF4y2Ba_EAgydF4y2Ba(即协议不终止的概率的上界为gydF4y2BaϵgydF4y2Ba_EAgydF4y2Ba)或条件光滑最小熵gydF4y2Ba\ ({H} _{\分钟}^{{\ε}_{年代 }}{({{{{{{{\ 男朋友{B }}}}}}}}|{{{{{{{\ 男朋友{米 }}}}}}}},\, E)} _{{\ρ}^{\ω}}\)gydF4y2Ba(在这里,gydF4y2Ba米gydF4y2Ba由寄存器组成gydF4y2BaTgydF4y2Ba，gydF4y2BaXgydF4y2Ba,gydF4y2BaYgydF4y2Ba)为一定数量的下界。通过识别寄存器gydF4y2Ba\ ({E} ^ {{\ '}} \)gydF4y2Ba在定理3中作为寄存器gydF4y2Ba米gydF4y2BaEgydF4y2Ba在稳健性判据中，可以选择稳健性误差gydF4y2BaεgydF4y2Ba_苏gydF4y2Ba是gydF4y2Ba

在这种情况下，EAT上限Pr[Ω] bygydF4y2BaϵgydF4y2Ba_EAgydF4y2Baor -与量子剩余散列引理结合-保证了稳健条件中的跟踪距离项(用于协议未中止的状态)小于2(gydF4y2BaϵgydF4y2Ba_{年代gydF4y2Ba}+gydF4y2BaκgydF4y2Ba)。因此，我们选择了gydF4y2BaεgydF4y2Ba_苏gydF4y2Ba确保协议在EAT考虑的两种情况下都是健全的。在这项工作中，我们选择gydF4y2BaεgydF4y2Ba_苏gydF4y2Ba=gydF4y2BaϵgydF4y2Ba_EAgydF4y2Ba= 2 (gydF4y2BaϵgydF4y2Ba_{年代gydF4y2Ba}+gydF4y2BaκgydF4y2Ba),gydF4y2BaκgydF4y2Ba选择使预期净扩张率最大化。gydF4y2Ba

现在我们将讨论定理1的技术细节。首先，为了应用EAT，重要的是要确保在协议执行过程中满足所谓的马尔可夫条件。更准确地说，我们希望每一轮都是这样gydF4y2Ba我gydF4y2Ba∈gydF4y2Ba(gydF4y2BangydF4y2Ba，我们需要gydF4y2Ba

在哪里gydF4y2Ba我gydF4y2Ba（gydF4y2Ba一个gydF4y2Ba:gydF4y2BaBgydF4y2Ba∣gydF4y2BaCgydF4y2Ba)表示之间的量子互信息gydF4y2Ba一个gydF4y2Ba和gydF4y2BaBgydF4y2Ba条件在gydF4y2BaCgydF4y2Ba。在这里,gydF4y2BaBgydF4y2Ba_{［gydF4y2Ba我gydF4y2Ba]gydF4y2Ba}表示字符串(gydF4y2BaBgydF4y2Ba_1gydF4y2Ba,gydF4y2BaBgydF4y2Ba_2gydF4y2Ba……gydF4y2BaBgydF4y2Ba_我gydF4y2Ba)，描述从第一轮到第一轮的测量结果gydF4y2Ba我gydF4y2Bath。gydF4y2BaXgydF4y2Ba_{［gydF4y2Ba我gydF4y2Ba]gydF4y2Ba},gydF4y2BaYgydF4y2Ba_{［gydF4y2Ba我gydF4y2Ba]gydF4y2Ba},gydF4y2BaTgydF4y2Ba_{［gydF4y2Ba我gydF4y2Ba]gydF4y2Ba}定义相似。为了加强协议中的马尔可夫条件，我们按顺序实现每一轮，并从可信的私有随机种子中选择每一轮的输入，该种子独立于前几轮的输入和输出。我们还隔离了设备，这样伊芙在执行协议时就不会获得额外的量子侧信息。gydF4y2Ba

我们需要的下一个要素是所谓的最小权衡函数gydF4y2BafgydF4y2Ba(关于其正式定义，请参阅参考文献定义II.4。gydF4y2Ba^30.gydF4y2Ba)。简而言之，最小权衡函数是最坏情况下单轮条件冯·诺依曼熵的仿射下界gydF4y2BaHgydF4y2Ba（gydF4y2BaBgydF4y2Ba_我gydF4y2Ba∣gydF4y2BaXgydF4y2Ba_我gydF4y2Ba,gydF4y2BaYgydF4y2Ba_我gydF4y2Ba,gydF4y2BaTgydF4y2Ba_我gydF4y2Ba,gydF4y2BaRgydF4y2Ba)，即与上面的概率分布“兼容”gydF4y2Ba\({{{{{{{\ mathcal {C }}}}}}}} =\{\ 补\ 0 \ 1 \}\)gydF4y2Ba对于随机变量gydF4y2BaCgydF4y2Ba_我gydF4y2Ba。在这里,gydF4y2BaRgydF4y2Ba量子寄存器是否与圆形的预测态同构gydF4y2Ba我gydF4y2Ba。gydF4y2Ba

为了构造最小权衡函数，我们遵循参考文献中给出的框架。gydF4y2Ba^30.gydF4y2Ba在与设备无关的随机展开的背景下。这里的一个关键区别是，我们使用了在ref的定理14中导出的条件冯·诺依曼熵的界。gydF4y2Ba^48gydF4y2Ba

而不是参考中使用的基于条件最小熵的边界。gydF4y2Ba^30.gydF4y2Ba。而两个边界都是基于猜测概率gydF4y2BapgydF4y2Ba_ggydF4y2Ba（gydF4y2BaBgydF4y2Ba_我gydF4y2Ba∣gydF4y2BaXgydF4y2Ba_我gydF4y2Ba= 0,gydF4y2BaYgydF4y2Ba_我gydF4y2Ba= 0,gydF4y2BaTgydF4y2Ba_我gydF4y2Ba= 0,gydF4y2BaRgydF4y2Ba)，我们在这里使用的边界明显比在进行实验的参数体系中由条件最小熵给出的边界更紧。另一个优点是，我们使用的边界已经是线性的，因此，我们不需要执行在ref中执行的线性化。gydF4y2Ba^30.gydF4y2Ba得到一个仿射最小权衡函数。gydF4y2Ba

为了约束猜测概率，我们使用了文献中提出的半确定规划(SDP)技术。gydF4y2Ba^31gydF4y2Ba而不是navascue - pironio - acin (NPA)层次结构gydF4y2Ba^{49gydF4y2Ba，gydF4y2Ba50gydF4y2Ba}用于ref。gydF4y2Ba^30.gydF4y2Ba。这两种技术都是SDP松弛的两个相似层次，它们约束了量子相关集;后者适用于与设备无关的场景，而前者适用于我们协议中考虑的准备-测量体系结构。为了达到固定的放松水平gydF4y2BakgydF4y2Ba，一个给定的P&M游戏gydF4y2Ba\({{{{{{{\ mathcal {G }}}}}}}}\)gydF4y2Ba，以得分系数为特征gydF4y2Ba\({w}_{b,x,y} =q(x，\， y){\delta}_{b，{b}_{xy}}\)gydF4y2Ba，以及一定的获胜概率gydF4y2BaνgydF4y2Ba时，猜测概率的SDP有以下原始形式gydF4y2Ba

在这里,gydF4y2Ba\ ({\ {{M} _ {b | y} \}} _ {b, y} \)gydF4y2Ba表示Bob的POVM元素，gydF4y2Ba\({\{{\π}_ {e} \}} _ {e} \)gydF4y2Ba表示作用于系统的POVM元素gydF4y2BaRgydF4y2Ba和gydF4y2Ba\({{{{{{{\ mathcal {U }}}}}}}}:\ 左| {\ psi} _ {x} \正确\纠正\ \左|{\φ}_ {x} \ \纠正\)gydF4y2Ba表示连接Alice和Bob的未知量子通道的等距。由(的对偶解gydF4y2Ba17gydF4y2Ba)，则可以得到该形式的猜测概率的一个上界gydF4y2Ba

在这里,gydF4y2BapgydF4y2Ba=(1−gydF4y2BapgydF4y2Ba,gydF4y2BapgydF4y2Ba)为设备的评分分布gydF4y2BaλgydF4y2Ba_νgydF4y2Ba和gydF4y2BacgydF4y2Ba_νgydF4y2Ba为SDP的双解(gydF4y2Ba17gydF4y2Ba)。我们强调gydF4y2BaνgydF4y2Ba是一个我们可以自由选择的参数，它不一定是设备获得的实际获胜概率。gydF4y2Ba

跟随ref.中的参数。gydF4y2Ba^30.gydF4y2Ba，考虑仿射函数gydF4y2BaggydF4y2Ba_νgydF4y2Ba，它映射了一个分布gydF4y2Ba\({{{{{{{\mathcal{C}}}}}}}}\setminus \{\perp \}\)gydF4y2Ba一个实数gydF4y2Ba

在哪里gydF4y2BaegydF4y2Ba_cgydF4y2Ba概率分布在哪里gydF4y2BacgydF4y2Ba第一个元素是1，其他元素都是0。然后，对于某个常数gydF4y2BaugydF4y2Ba_⊥gydF4y2Ba我们稍后会确定，下面的函数gydF4y2BafgydF4y2Ba_νgydF4y2Ba是最小权衡函数吗gydF4y2Ba

为了找到导致协议被接受的所有分布的最坏情况，我们重复引用中给出的参数。gydF4y2Ba^9gydF4y2Ba在这里。首先，我们使用协议被接受的条件，freqgydF4y2Ba_CgydF4y2Ba(0)≤gydF4y2BaγgydF4y2Ba(1−gydF4y2BaωgydF4y2Ba+gydF4y2BaδgydF4y2Ba)，从而推导出如果gydF4y2BaugydF4y2Ba_⊥gydF4y2Ba≥gydF4y2BaggydF4y2Ba_νgydF4y2Ba（gydF4y2BaegydF4y2Ba_0gydF4y2Ba)，然后我们有gydF4y2Ba

现在，我们要求这样做gydF4y2BaugydF4y2Ba_⊥gydF4y2Ba≤gydF4y2BaggydF4y2Ba_νgydF4y2Ba（gydF4y2BaegydF4y2Ba_1gydF4y2Ba)，因此，右边的第二项可以省略gydF4y2Ba

这是随着gydF4y2BaugydF4y2Ba_⊥gydF4y2Ba因此，最好是修复gydF4y2BaugydF4y2Ba_⊥gydF4y2Ba=gydF4y2BaggydF4y2Ba_νgydF4y2Ba（gydF4y2BaegydF4y2Ba_1gydF4y2Ba)。我们有gydF4y2Ba

调整后的分数gydF4y2Ba\ \(波浪号{{{{{{{{\ boldsymbol{\ω }}}}}}}}} =( 1 - \ω+ \三角洲、\ \ω-δ)\ \)gydF4y2Ba。这样，我们就得到了函数gydF4y2BafgydF4y2Ba定理1。gydF4y2Ba

最后，我们必须计算修正项gydF4y2BaVgydF4y2Ba和gydF4y2BaKgydF4y2Ba。为此，我们需要考虑最小权衡函数的几个性质。它们如下gydF4y2Ba

1. 1.gydF4y2Ba

   所有概率分布的最大值gydF4y2Ba

在哪里gydF4y2Ba\({{{{{{{{\ mathcal {P }}}}}}}}}_{{{{{{{{\ mathcal {C }}}}}}}}}\)gydF4y2Ba是所有有效概率分布的集合。gydF4y2Ba

1. 2.gydF4y2Ba

   最小的所有协议关于分布gydF4y2Ba

其中Γ表示表单的分布集(gydF4y2BaγgydF4y2BaωgydF4y2Ba， 1−gydF4y2BaγgydF4y2Ba)。我们称这种分布为关于分布的协议。gydF4y2Ba

1. 3.gydF4y2Ba

   关于分布的所有协议的最大方差gydF4y2Ba

为了计算这些量，我们考虑的最大值和最小值gydF4y2BaggydF4y2Ba_νgydF4y2Ba(在所有发行版中)作为gydF4y2Ba

在哪里gydF4y2Ba\({\λ}_{\分钟}= \ mathop{\分钟}\ limits_ {c }{{{{{{{{\ boldsymbol{\λ }}}}}}}}}_{\ ν}\)gydF4y2Ba和gydF4y2Ba\({\λ}_{\马克斯}= \ mathop{\马克斯}\ limits_ {c }{{{{{{{{\ boldsymbol{\λ }}}}}}}}}_{\ ν}\)gydF4y2Ba。注意选择gydF4y2BaggydF4y2Ba_νgydF4y2Ba（gydF4y2BaegydF4y2Ba_0gydF4y2Ba)≤gydF4y2BaugydF4y2Ba_⊥gydF4y2Ba=gydF4y2BaggydF4y2Ba_νgydF4y2Ba（gydF4y2BaegydF4y2Ba_1gydF4y2Ba)暗示gydF4y2Ba\({你}_{\补 } ={{{{{{{\ rm{马克斯 }}}}}}}}[{ g} _{\ν}]\)gydF4y2Ba。因此，我们正在处理与参考中考虑的相似的最小权衡函数。gydF4y2Ba^{29gydF4y2Ba，gydF4y2Ba30.gydF4y2Ba}，其中我们有如下关系gydF4y2Ba

根据上述关系，我们可以计算修正项gydF4y2BaVgydF4y2Ba和gydF4y2BaKgydF4y2Ba。ref。gydF4y2Ba^30.gydF4y2Ba，修正期gydF4y2BaVgydF4y2Ba（gydF4y2BaγgydF4y2Ba,gydF4y2BafgydF4y2Ba_νgydF4y2Ba)由gydF4y2Ba

另一方面，另一个修正项gydF4y2BaKgydF4y2Ba（gydF4y2BaβgydF4y2Ba,gydF4y2BaγgydF4y2Ba,gydF4y2BafgydF4y2Ba_νgydF4y2Ba)由gydF4y2Ba

在指定了函数之后gydF4y2BafgydF4y2Ba_νgydF4y2Ba，gydF4y2BaVgydF4y2Ba和gydF4y2BaKgydF4y2Ba，我们现在可以应用定理1和定理3来证明我们的QRNG协议的可靠性。完成了该方案的随机性证明。gydF4y2Ba

输入随机gydF4y2Ba

在前一节中，我们已经展示了如果提取的长度gydF4y2BaℓgydF4y2Ba根据式(gydF4y2Ba13gydF4y2Ba)，我们的QRNG协议可以安全地生成随机性。然而，为了使我们的QRNG协议实际有用，我们还可能要求，平均而言，它产生的随机性比运行该协议所消耗的随机性更多。gydF4y2Ba

在这项工作中，当我们考虑随机抽取的强提取器时，考虑选择输入所消耗的随机性就足够了gydF4y2BaTgydF4y2Ba,gydF4y2BaXgydF4y2Ba和gydF4y2BaYgydF4y2Ba因为我们可以将提取程序种子作为输出的一部分。由于最佳输入分布是有偏差的，因此可以使用有偏差的随机种子或将均匀随机种子转换为有偏差的种子(例如，使用间隔算法)gydF4y2Ba^51gydF4y2Ba)。我们表示gydF4y2Ba预期gydF4y2Ba用于生成输入的随机位串的长度gydF4y2BaℓgydF4y2Ba_在gydF4y2Ba。期望的输入随机性gydF4y2BaℓgydF4y2Ba_在gydF4y2Ba大约是输入的香农熵(直到一些对于大块大小可以忽略不计的小开销)gydF4y2Ba

我们使用了每一轮的输入都是独立于前几轮的输入的事实，我们还使用了香农熵的链式法则。在这里,gydF4y2BahgydF4y2Ba_2gydF4y2Ba（gydF4y2BaγgydF4y2Ba)为二进制熵函数，gydF4y2BaHgydF4y2Ba（gydF4y2Ba问gydF4y2Ba)为输入分布的香农熵{gydF4y2Ba问gydF4y2Ba（gydF4y2BaxgydF4y2Ba,gydF4y2BaygydF4y2Ba)}gydF4y2Ba_{xgydF4y2Ba，gydF4y2BaygydF4y2Ba}。gydF4y2Ba

零差检测器建模和特性gydF4y2Ba

我们从光学损耗和电子噪声两个方面对零差探测器进行建模。gydF4y2Ba

光学损耗主要由两部分引起。由于两个光电二极管的效率不匹配和BS劈裂比不完美，导致BS的插入损耗和零差检测不平衡。gydF4y2Ba

我们首先用光功率计(EXFO PM-1100)和源测量单元(Keysight U2722A)描述了光电二极管的光子检测效率，其中包括光电二极管的量子效率、光电二极管的耦合损耗和光纤尾GRIN透镜的插入损耗。gydF4y2Ba

使用的GRIN透镜在1250-1650 nm范围内涂有抗反射涂层，平均反射<0.2%。此外，输出光束的束腰直径约为10µm，远小于我们的PD的有源区直径(100µm)。通过对两个光电二极管的工作电压施加反向偏置，从激光器输入恒定功率的光，并通过源测量单元测量光电流，测量两个光电二极管的检测效率，包括耦合损耗和插入损耗。通过测量光电流与输入功率之比，推导出两个光电二极管的效率分别为98.3%和98.8%。gydF4y2Ba

测得分束器的劈裂比为50.4:49.6，插入损耗为0.2 dB。通过将分束器与pd相匹配，并仔细平衡两臂的振幅，我们使用可变光衰减器(Yokogawa AQ2200-311A)逐渐增加输入LO功率，并获得噪声测量。频域测量使用频谱分析仪(罗德施瓦茨FSV40)，分辨率带宽为1 MHz，视频带宽为5 MHz。为了测量噪声方差和间隙，使用了示波器(Tektronix MSO64 BW 2.5 GHz)。gydF4y2Ba

表征结果如图所示。gydF4y2Ba1gydF4y2Bad, e.在10mw LO输入时，获得的间隙为16.94 dB。在零差探测器的电子噪声具有高斯分布且与测量光信号无关的假设下，我们遵循文献中提出的模型。gydF4y2Ba^52gydF4y2Ba并将电子噪声的影响等效为效率损失。在本例中，估计等效效率为97.98%。gydF4y2Ba

综合考虑所有因素，我们的零差探测器的总有效效率达到91.7%。gydF4y2Ba

双模相干态gydF4y2Ba

本系统采用双模相干态制备量子态。在这里，我们给出了双模相干态正交算子的基本形式，并证明了正交算子可以通过组合各个时间模的正交值来得到。gydF4y2Ba

在不失一般性的前提下，我们定义了早期和晚期时间模态的产生(湮灭)算符gydF4y2Ba\({\帽子{一}}_ {e} ^{{{{\匕首}}}}\)gydF4y2Ba（gydF4y2Ba\({\帽子{一}}_ {e} \)gydF4y2Ba),gydF4y2Ba\({\帽子{一}}_ {l} ^{{{{\匕首}}}}\)gydF4y2Ba（gydF4y2Ba\({\帽子{一}}_ {l} \)gydF4y2Ba),分别。因此，由两种时间模式的相干态组成的量子态可以表示为:gydF4y2Ba

在哪里gydF4y2Ba\(|{\α}_ {t} | = \√6{|{\α}_ {e}{|} ^{2} + |{\α}_ {l} {|} ^ {2}} \)gydF4y2Ba和gydF4y2Ba\({\帽子{一}}_ {t} ^{{{{\匕首}}}}= \压裂{1}{\左|{\α}_ {t} \右|}({\α}_ {e}{\帽子{一}}_ {e} ^{{{{\匕首}}}}+{\α}_ {l}{\帽子{一}}_ {l} ^{{{{\匕首}}}})\)gydF4y2Ba分别表示新的双模相干态的振幅和产生算子。在我们这里，我们做到了gydF4y2Ba\(左\ |{\α}_ {l} \ \纠正= \左右| -{\α}_ {e} \ \纠正\)gydF4y2Ba，gydF4y2Ba\(|{\α}_ {t} | = \ sqrt {2} alpha | | \ \)gydF4y2Ba,gydF4y2Ba\({\帽子{一}}_ {t} ^{{{{\匕首}}}}= 1 / \√{2}({\帽子{一}}_ {e} ^{{{{\匕首}}}}-{\帽子{一}}_ {l} ^{{{{\匕首}}}})\)gydF4y2Ba。gydF4y2Ba

由此可得到双模相干态的正交算子(在Shot-Noise Unit中):gydF4y2Ba

因此，双模相干态的正交值gydF4y2Ba问gydF4y2Ba_tgydF4y2Ba满足gydF4y2Ba

制定P&M游戏gydF4y2Ba

以前，我们想当然地认为我们的QRNG协议指定了一个P&M游戏，用于测试设备是否按预期工作。然而，构建一款最适合证明随机性生成的游戏并非简单任务。在本节中，我们使用SDP对偶性来构造一个P&M博弈，它可以渐近地见证由完全输入-输出概率分布所证明的相同数量的随机性{gydF4y2BaPgydF4y2Ba（gydF4y2BabgydF4y2Ba∣gydF4y2BaxgydF4y2Ba,gydF4y2BaygydF4y2Ba)}gydF4y2Ba_{bgydF4y2Ba，gydF4y2BaxgydF4y2Ba，gydF4y2BaygydF4y2Ba}。我们的方法背后的思想是找到一个输入-输出概率分布的线性函数，它见证了Bob的测量所产生的随机性。然后，从这个线性函数，我们可以推导出输入分布gydF4y2Ba问gydF4y2Ba（gydF4y2BaxgydF4y2Ba,gydF4y2BaygydF4y2Ba)和获胜的输出gydF4y2BabgydF4y2Ba_{xgydF4y2BaygydF4y2Ba}。类似的结构已被用于设备无关的量子信息处理中，以构造用于证明随机性的最优贝尔不等式gydF4y2Ba^{53gydF4y2Ba，gydF4y2Ba54gydF4y2Ba}和自我测试gydF4y2Ba^55gydF4y2Ba。gydF4y2Ba

渐近地，我们期望完整的输入-输出概率分布应该是见证随机性的最佳分布，因为它包含有关设备行为的完整统计信息。现在让我们假设预期的输入-输出概率分布是已知的(通过对诚实的实现建模或在协议之前校准设备)。为了构造一个能够最优地证明随机性数量的博弈，我们将考虑以下SDP对完全输入-输出概率分布下的猜测概率。gydF4y2Ba

假设(的最优对偶解)gydF4y2Ba36gydF4y2Ba)gydF4y2BakgydF4y2Ba弛豫水平由gydF4y2Ba

在哪里gydF4y2BaξgydF4y2Ba_0gydF4y2Ba与非统计约束相关联。任何可行的对偶解都是输入-输出分布的线性函数，它是猜测概率的上界。因此，SDP的可行对偶解集给出了一组猜测概率的线性上界gydF4y2Ba帽子\ ({\ d {}} _ {k} \)gydF4y2Ba家族中猜测概率的上限是最紧的吗(实际上，它是“紧”到半确定松弛?gydF4y2Ba^31gydF4y2Ba量子相关性的集合和任何对偶缺口)。gydF4y2Ba

现在，对于每对输入(gydF4y2BaxgydF4y2Ba,gydF4y2BaygydF4y2Ba)，我们定义gydF4y2Ba\ ({b} _ {xy} ^ {{\ '}} \)gydF4y2Ba和gydF4y2Ba\ ({b} _ {xy} ^ {{\ ' \ '}} \)gydF4y2Ba这样gydF4y2Ba\ \ (xi ({b} _ {xy} ^ {{\ '}}, \, x, \, y) \通用电气\ xi ({b} _ {xy} ^ {{\ ' \ '}}, \, x, \, y) \)gydF4y2Ba。我们考虑gydF4y2Ba

在第一个等式中，我们使用归一化约束。注意到我们只是减去了一个常数gydF4y2Ba帽子\ ({\ d {}} _ {k} \)gydF4y2Ba，表达式(gydF4y2Ba38gydF4y2Ba)在猜测概率上仍然是一个近乎严密的见证。最后，我们还可以将上面的表达式除以一个常数和得到的表达式gydF4y2Ba

与gydF4y2Ba

在猜测的概率上仍然是一个几乎紧密的见证。通过构造，{gydF4y2Ba问gydF4y2Ba（gydF4y2BaxgydF4y2Ba,gydF4y2BaygydF4y2Ba)}gydF4y2Ba_{xgydF4y2Ba，gydF4y2BaygydF4y2Ba}是有效的概率分布。此外,正如gydF4y2Ba\ ({b} _ {xy} ^ {{\ '}} \)gydF4y2Ba是这样定义的gydF4y2Ba帽子\ ({\ d {}} _ {k} \)gydF4y2Ba(因此，猜测概率的界限)会更高gydF4y2Ba\(P({b}_{xy}^{{\prime}}|x，\， y)\)gydF4y2Ba增加，我们可以解释gydF4y2Ba\ ({b} _ {xy} ^ {{\ '}} \)gydF4y2Ba作为失败的结果(即，我们分配分数gydF4y2BaCgydF4y2Ba= 0)时输入gydF4y2BaxgydF4y2Ba和gydF4y2BaygydF4y2Ba都是被选中的gydF4y2Ba问gydF4y2Ba（gydF4y2BaxgydF4y2Ba,gydF4y2BaygydF4y2Ba)表示选择这对输入的概率。在这种情况下，是游戏gydF4y2Ba\({{{{{{{\ mathcal {G }}}}}}}}\)gydF4y2Ba定义为Alice和Bob选择输入(gydF4y2BaxgydF4y2Ba,gydF4y2BaygydF4y2Ba)概率gydF4y2Ba问gydF4y2Ba（gydF4y2BaxgydF4y2Ba,gydF4y2BaygydF4y2Ba)，胜出的结果由gydF4y2Ba\({b}_{xy} ={b}_{xy}^{{\prime\prime}}\)gydF4y2Ba。gydF4y2Ba

我们上面所描述的游戏结构几乎是最理想的gydF4y2Ba生成的gydF4y2Ba随机性。然而，该构造可能不会最小化选择输入所消耗的随机性，因此，它在扩展随机性方面的性能可能远远不是最优的。制定最大化净随机性扩展率的最佳游戏结构将是未来工作的一个有趣方向。gydF4y2Ba

随机抽取gydF4y2Ba

Toeplitz哈希利用一个Toeplitz矩阵，gydF4y2BaHgydF4y2Ba。Toeplitz矩阵是gydF4y2Ba米gydF4y2Ba×gydF4y2BangydF4y2Ba对角常数矩阵，它是通过将矩阵的第一列和第一行填充为均匀种子来构造的，表示为gydF4y2Ba年代gydF4y2Ba。因此，Toeplitz哈希所需的种子长度为gydF4y2BangydF4y2Ba+gydF4y2Ba米gydF4y2Ba−1位。托普利兹矩阵gydF4y2BaHgydF4y2Ba可以表示为gydF4y2Ba

哈希是通过将原始位表示为列向量并与Toeplitz矩阵执行矩阵向量乘法来完成的。我们使用0.00455的比特生成率计算并构造Toeplitz矩阵gydF4y2BaHgydF4y2Ba使用参数gydF4y2Ba米gydF4y2Ba= 45和gydF4y2BangydF4y2Ba= 10000。gydF4y2Ba

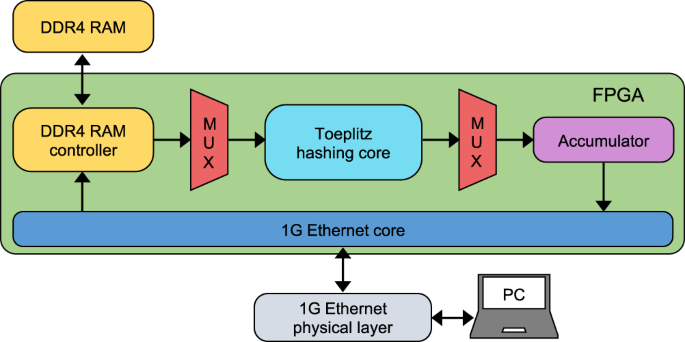
现场可编程门阵列(FPGA)是Toeplitz哈希算法的实现平台。我们的FPGA后处理原理图如图所示。gydF4y2Ba5gydF4y2Ba。原始数据存储在个人计算机(PC)上，并通过1G以太网以大约600mbits的批量发送到FPGA。FPGA上的处理系统(PS)在接收到一批原始数据后，将10kbits的数据发送到可编程逻辑(PL)，在PL中数据将进一步分成10批，每批1kbits。原始数据和种子的多路复用是通过流水线完成的，Toeplitz哈希算法是并行执行的。然后PS从PL接收45位的输出，并向PL发送一组新的10千比特的数据，一直重复，直到当前批处理中的所有数据都已处理完毕。然后PS通过以太网将提取出的当前批的随机数发送到PC，并等待新的批，直到所有10.622 Gbits的原始数据处理完毕。gydF4y2Ba