简介

自新冠肺炎疫情爆发以来，疫情在全球多个国家和地区迅速蔓延，世界卫生组织于2020年1月30日宣布新冠肺炎为国际关注的突发公共卫生事件(PHEIC)。根据美国约翰霍普金斯大学公布的数据，截至2020年10月11日，全球188个国家和地区新冠肺炎确诊病例37213592例，死亡1072959例。为了减少COVID-19的影响，预测COVID-19的趋势，如COVID-19的高峰和传播阶段，对政府制定防控策略，及时采取措施，分配医疗资源具有重要意义。已有许多研究预测了疫情在各个国家和地区的发展趋势。这些研究大致可以分为三类:统计建模方法、基于人工智能的方法和数学流行模型。

统计建模方法通过病例报告和其他数据统计估计主要流行参数，包括基本再现数(R \ ({} _ {0} \))、潜伏期、序列间隔、生成时间等，然后利用指数增长等数学模型预测疫情曲线。赵等。1使用指数增长模型拟合中国COVID-19疫情曲线，结果显示该病毒可能导致疫情爆发。Sanche等人。2收集了大量病例报告，以估计关键的流行病学参数，这表明需要及早采取强有力的控制措施，以阻止病毒的传播。派克和塞尼3.根据在中国观察到的死亡率统计数据计算其他国家的未来趋势，表明可能存在一个有效的公共卫生干预门槛。李等人。4采用高斯分布对中国湖北省新冠肺炎疫情的传播进行了分析，并预测了韩国、意大利和伊朗的疫情趋势。结果显示了疫情的演变，并发现实施控制将产生重大影响。Tang等。5利用时间依赖性暴露和诊断率估算了中国每天的基本感染数量，发现最佳措施是持续和严格的自我隔离。也有一些研究使用统计建模的方法6，7，8，9，10．而统计建模方法适合于在疫情早期对疫情进行粗略估计。随着疫情的发展，这些疫情参数在不同国家和地区是不断变化的，这就导致了这种预测只是不能反映疫情的实际情况。

人工智能预测方法是一种新兴的新冠病毒预测方法，用于预测新冠病毒在时间和空间上的传播方式。Hu等。11使用改进的堆叠式自动编码器对流行病的传播动态进行建模，实时预测中国COVID-19确诊病例。Yang等。12将2003年SARS疫情数据分为3天为输入，采用长短期记忆网络模型(LSTM)进行训练，对中国大陆新型冠状病毒疫情进行预测。弗里斯顿等人。13开发了基于人口动态的COVID-19动态因果模型，该模型利用了贝叶斯模型比较。Ardabili等人。14对比分析了新冠肺炎疫情预测的机器学习模型和软计算模型，结果表明，基于多层感知器和自适应网络的模糊推理系统具有较高的长期预测泛化能力。阿罗拉等人。15利用基于LSTM的多种深度学习模型对印度新冠肺炎阳性报告病例数进行预测，结果表明Bi-LSTM的预测效果最好，卷积LSTM的预测效果最差。虽然基于人工智能的方法精度很高，预测曲线可以很好地拟合，但基于人工智能的方法仍然存在两个问题。一是由于缺乏训练数据，预测方法不能很好地进行训练以达到预期效果，特别是在大流行初期16，17，18．另一个问题是这种方法的过拟合问题，因此可能无法可靠地预测。因此，迄今为止，大多数研究都是使用已建立的流行病学数学模型进行跟踪和预测。

有两种典型的流行病学数学模型，包括SIR和SEIR(易感、暴露、感染和去除)。许多研究对这两种流行病学数学模型进行了调整，以满足特定需求，并分析了COVID-19的传播动态。对模型的修改分为几种类型:在原有模型的基础上增加新的状态或修改模型参数，将额外的外部数据集成到模型中，增加非药物干预对模型的影响等。Liu等。19根据SIR模型添加无症状的感染者，并利用中国早期报告的病例数据预测累计报告病例数。该模型的主要特点是对政府主要公共政策的时机进行建模。彭等人。20.等人提出了广义的SEIR模型，重新制定了新的隔离状态，并考虑了预防措施的效果，并分析了中国五个不同地区的疫情。但由于检测方法和诊断标准的限制，难以估计未报告病例和暴露病例，难以获得准确的病例数。这些数字在研究过程中被视为隐变量。Sun等人。21建立了时变系数vSIR模型，以反映政府干预对模型参数的影响。Chen等。22建立了COVID-19感染者不可检出的时变SIR模型，利用两个有限脉冲响应滤波器跟踪和预测中国的感染者和康复人数。就结果而言，预测误差很小，但模型的训练是建立在数据充足的基础上，不适用于疫情的早期预测。Fanelli等人。23利用带死亡状态的SIRD模型预测中国、意大利和法国的疫情趋势，发现COVID-19的时间演化具有一定的普遍性，与地理变化联系不大，但本研究仅基于简单的定量模型来评估严格防疫的效果。此外，其他研究对SEIR模型进行了修改，例如考虑了人口迁移数据12，分析疏散航班上感染乘客的比例24等等。比斯瓦斯等人。25利用SIR模型对欧几里德网络上的中文数据进行拟合，结果表明，在模型中加入其他因素会使模型更加复杂。虽然这些修改流行病学模型的方法可用于评估流行病的传播和政府干预战略的影响，但这些模型需要引入额外的参数，并依赖于许多假设。同时，研究表明，复杂模型中未知参数数量的增加需要通过模型拟合来估计，这将导致模型预测的不确定性更高。因此，在模型选择过程中，简单模型可能比复杂模型更可靠26．另外，考虑到暴露案例数据的准确性难以保证，因此本文选择了常用的SIR模型。

在传统的SIR模型中，有两个关键参数反映了流行病的特征:感染率\ \ upbeta \ ()以及恢复速度\ \ upgamma \ ()．感染率\ \ upbeta \ ()表示每个易感人群随机感染\ \ upbeta \ ()每天的人;回收率\ \ upgamma \ ()表示受感染者恢复或死亡的概率为\ \ upgamma \ ()．这两个参数在传统SIR模型中是常数。当将其应用于现实世界时，他们往往无法测量和预测流行病的趋势。因此，许多研究将它们视为随时间变化的函数21，22．

但由于不同国家和地区的疫情防控措施不同，以及疫情发展情况不同，手工选取的函数不适用于参数的实时变化。为了反映传染病模型关键参数的这一变化，我们建议使用一个时间窗口来动态测量关键参数，并以每日为基准，同时考虑到不同国家和地区在疫情期间采取的遏制措施所导致的不同发展水平。时间窗口指的是当天的前一段时间，这样测量模型参数就可以适应不同的国家和地区。而\ \ upbeta \ ()而且\ \ upgamma \ ()不能完全衡量病毒在传播过程中的容量，通常我们会使用基本数字R \ ({} _ {0} \)反映疫情演变情况。同时，我们也用指数增长速度作为指标来反映病毒传播过程中的指数增长。通过结合这两个指标，我们可以跟踪和预测\ \ upbeta \ ()而且\ \ upgamma \ ()．基于这一思想，我们提出了一种时间窗SIR预测模型(TW-SIR)，该模型能够实时捕捉、跟踪和预测疫情参数的动态变化。我们在中国、韩国、意大利、西班牙、巴西、德国和法国的COVID-19历史数据上应用了TW-SIR模型，我们有兴趣解决以下三个关于COVID-19的重要问题。

  • RQ1: TW-SIR模型在测量R \ ({} _ {0} \)在流行的过程中呈指数级增长?与公式推导法相比，TW-SIR的参数测量是否更合理有效?

  • RQ2: TW-SIR模型对COVID-19疫情的预测效果如何?

  • RQ3: TW-SIR能适应第二波感染吗?

数值结果分析结果令人鼓舞。结果表明，该模型能有效测量传染病传播过程中各参数的实时变化，包括基本感染数R \({} _{0} \左(t \) \)呈指数增长\ \ (Ex (t))．实验结果表明，TW-SIR在参数测量方面优于公式推导法。预测新冠肺炎单日感染人数的错误率在5%以内。同时，该模型能够适应传统SIR模型所不能适应的第二波感染。本研究对了解新冠肺炎疫情的传播规律，指导制定防控策略和措施具有重要意义。

本文的其余部分组织如下:在第二部分，我们提出了TW-SIR模型。在第三部分，我们进行了一些数值实验，并对实验结果进行了分析，以说明我们的模型的有效性。然后，在“讨论，我们提出了一些讨论和建议。最后，最后一节是对论文的总结。

方法

SIR流行模型

易感-感染-恢复(SIR)模型27是最简单常用的流行病模型之一。模型由三个部分组成:\ (\):易感人群数量，我\ \ ():感染个体数量，\ (R \)被移除(和免疫)或死亡个体的数量。SIR流行模型可用以下常微分方程表示:

$ $ \压裂{dS (t)} {dt} = - \压裂{\β(t) S (t)} {N} $ $
(1)
$ $ \压裂{dI (t)} {dt} = \压裂{\β(t) S (t)} {N} - \γ(t) $ $
（2）
$ $ \压裂{(t)博士}{dt} = \γ(t) $ $
（3）
$ $ N = S \左(t \右)+ I \左(t \右)+ R (t) $ $
（4）

其中,左(t \ (S \ \) \)，左(t \(我\ \)\)而且左(t \ (R \ \) \)，分别表示的函数\ (\)，我\ \ ()而且\ (R \)与时间有关\ \ (t)，且它们的和满足Eq. (4）;\ (N \)表示人口总数;β\ (\ \)表示感染率的概率，表示每个易感人群随机感染β\ (\ \)每天都有人。回收率\γ(\ \)表示受感染者恢复或死亡的概率为\γ(\ \)．

SIR模型虽然简单，但在许多研究中对它的分析和使用通常表明，它可以捕捉到流行病的趋势和总体特征。在传统的SIR模型中，\ \ upbeta \ ()而且\γ(\ \)是反映流行病特征的参数，它们是常数。但是，如果参数是恒定的，当应用到现实世界时，往往无法测量和预测流行病的发展趋势。因此，许多研究将它们视为随时间变化的函数，并使用方程来推导它们。考虑到在疫情发展过程中，不同国家和地区的SIR模型参数都在实时变化。为了反映疫情模型参数的变化，本文提出了TW-SIR预测模型，该模型能够实时捕捉、跟踪和预测疫情参数的动态变化。我们将在下一节中详细介绍这个模型。

时间窗SIR模型

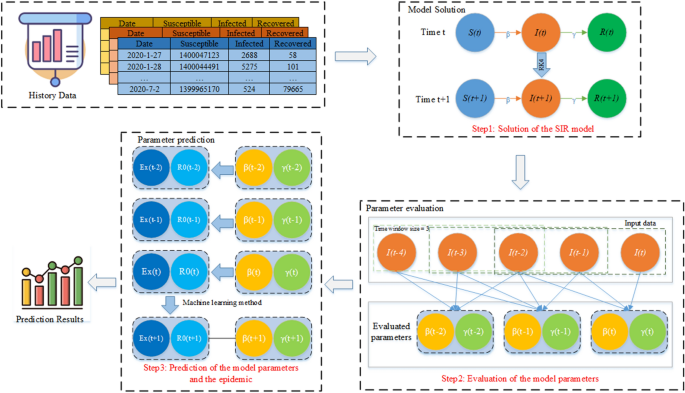
为了表示SIR模型中参数的变化，我们提出了一种基于时间窗口的SIR模型(TW-SIR)，该模型将历史数据分割为一个时间窗口段。该方法的目的是捕获的实时变化R \ ({} _ {0} \)还有指数增长速度\(\)交货．TW-SIR模型基于对历史数据的流行病学参数每天通过一个时间窗口的变化进行评估，解决了公式推导法无法实时测量的问题。数字1展示了模型的主要工作流程。

图1
图1

TW-SIR模型的主要工作流程。

全尺寸图像

如图所示。1， TW-SIR模型主要由模型求解、参数评价和参数预测三部分组成。具体流程如下。

步骤1:SIR模型的求解。首先，TW-SIR模型的历史数据输入包括易感人群、感染人群和康复人群的每日数量和数据，并根据时间窗口大小对数据进行划分。对于指定时间窗口内的数据，采用龙格-库塔方法对SIR模型进行数值求解。

第二步:模型参数评估。基于时间窗口内的历史数据，采用最小二乘法设置模型参数的初值，然后遍历和搜索模型参数，表示基本复制数的变化R \ ({} _ {0} \)还有指数增长速度\(\)交货在历史数据中。

步骤3:模型参数和疫情预测。基于参数评估得到的现有参数值，结合基本再现数，采用机器学习方法对未来参数值进行跟踪预测R \ ({} _ {0} \)呈指数增长\(\)交货．最后，返回了疫情的预测结果。

TW-SIR的目的是评估疫情参数的变化，以预测疫情的发展趋势。在本节的其余部分中，我们将详细描述每个部分的内容。

模型的解决方案

模型求解的作用是对SIR模型方程进行数值求解，便于后续参数评价。由于SIR模型方程是耦合的非线性常微分方程，很难找到方程的解析解。虽然可以用隐式形式导出方程的解析解，但求解过程复杂，实际应用也有局限性28．与解析解相比，数值解等方法在这类研究问题中更常用，也更有效。本文采用数值求解方法，即龙格-库塔法对SIR模型进行数值求解。龙格-库塔方法是一种高精度的单步算法，其经典方法是四阶龙格-库塔方法(RK4)。RK4对时间间隔进行划分\ \ (t)而且\ (t + 1 \)分为四个子区间，通过计算这些子区间点的斜率值并将其加权为平均斜率来求解常微分方程。对于SIR模型的三种状态，我们使用RK4对式中的微分方程进行修正(1- - - - - -3.)转化为离散微分方程:

$ $ S \离开(t + 1 \右)= S \左(t \右)+ \压裂{h({年代}_{1}^{^{\ '}}+ 2{年代}_{2}^{^{\ '}}+{2}_{3}^{^{\ '}}+{年代}_ {4}^ {^ {\ '}})}{6}$ $
（5）
$ $我\离开(t + 1 \右)=我\左(t \右)+ \压裂{h({我}_{1}^{^{\ '}}+ 2{我}_{2}^{^{\ '}}+我{2}_{3}^{^{\ '}}+{我}_ {4}^ {^ {\ '}})}{6}$ $
(6）
$ $ R \离开(t + 1 \右)= R \左(t \右)+ \压裂{h ({R} _ {1} ^ {^ {\ '}} + 2 {R} _ {2} ^ {^ {\ '}} + {2 R} _ {3} ^ {^ {\ '}} + {R} _ {4} ^ {^ {\ '}})} {6} $ $
(7）

在哪里\ (\ mathrm {h} \)是步长，\({} _{我}^ {^ {\ '}}\)，\({我}_{我}^ {^ {\ '}}\)而且R \({} _{我}^ {^ {\ '}}\)（\ (\ mathrm{我}= \ mathrm {1,2}, \ mathrm{3、4}\))，分别表示在区间[t,t + 1]中的四个子区间的斜率左(t \ (S \ \) \)，左(t \(我\ \)\)而且左(t \ (R \ \) \)，可由公式计算。（8- - - - - -11）

左$ $ \ \{{\开始{数组}{l * {20}} {S_{1} ^{\ '} = - \压裂{{β\ S (t)我(t)}} {N}} \ hfill \ \ {I_{1} ^{\ '} = \压裂{{β\ S (t)我(t)}} {N} - \伽马我(t)} \ hfill \ \ {R_{1} ^{\ '} = \γ(t)} \ hfill \ \ \{数组}}结束\ $ $
（8）
$ $ \左\{{\开始{数组}{l * {20}} {S_{2} ^{\ '} = - \压裂{{\β\离开({年代\左(t \右)+ \压裂{{hS_{1} ^{\ '}}}{2}} \) \离开({我\左(t \右)+ \压裂{{hI_{1} ^{\ '}}}{2}} \右)}}{N}} \ hfill \ \ {I_{2} ^{\ '} = \压裂{{\β\离开({年代\左(t \右)+ \压裂{{hS_{1} ^{\ '}}}{2}} \) \离开({我\左(t \右)+ \压裂{{hI_{1} ^{\ '}}}{2}} \右)}}{N} - \伽马\离开({我\左(t \右)+ \压裂{{hI_{1} ^{\ '}}}{2}} \右)}\ hfill \ \ {R_{2} ^{\ '} = \γ\离开({我\左(t \右)+ \压裂{{hI_{1} ^{\ '}}}{2}} \右)}\ hfill \ \ \{数组}}结束\ $ $
（9)
$ $ \ \{\离开开始{数组}{1}{年代}_{3}^{^{\ '}}= - \压裂{\β(S \左(t \右)+ \压裂{h{年代}_{2}^{^{\ '}}}{2})(我\左(t \右)+ \压裂{h{我}_ {2}^ {^ {\ '}}}{2})}{N} \ \{我}_{3}^{^{\ '}}= \压裂{\β(S \左(t \右)+ \压裂{h{年代}_{2}^{^{\ '}}}{2})(我\左(t \右)+ \压裂{h{我}_ {2}^ {^ {\ '}}}{2})}{N} - \γ(我\左(t \右)+ \压裂{h{我}_ {2}^ {^ {\ '}}}{2})\ \ {R} _{3} ^{^{\ '}} = \γ(我\左(t \右)+ \压裂{h{我}_{2}^{^{\ '}}}{2})\结束数组{}\ $ $
（10）
$ $ \ \{\离开开始{数组}{1}{年代}_{4}^{^{\ '}}= - \压裂{\β(S \左(t \右)+ h{年代}_{3}^{^{\ '}})(我\左(t \右)+ h{我}_ {3}^ {^ {\ '}})}{N} \ \{我}_{4}^{^{\ '}}= \压裂{\β(S \左(t \右)+ h{年代}_{3}^{^{\ '}})(我\左(t \右)+ h{我}_ {3}^ {^ {\ '}})}{N} - \γ(我\左(t \右)+ h{我}_ {3}^ {^ {\ '}})\ \ {R} _{4} ^{^{\ '}} = \γ(我\左(t \右)+ h{我}_{3}^{^{\ '}})\结束数组{}\ $ $
（11）

由上式可知，β\ (\ \)而且\γ(\ \)代入SIR模型进行数值求解。的三个功能左(t \ (S \ \) \)，左(t \(我\ \)\)而且左(t \ (R \ \) \)满足Eq. (4)．

参数评估

参数评价部分主要是表征感染率的变化β\ (\ \)以及回收率\γ(\ \)在历史数据中随时间推移，从而便于后续参数预测。首先根据时间窗的大小对历史数据进行划分，然后在时间窗内设置模型参数的初始值，然后遍历搜索模型参数，最后通过评价得到每天的最佳模型参数。一个时间\β(t) (\ \)而且\γ(t) (\ \)函数被用来代替β\ (\ \)而且\γ(\ \)SIR模型中，可获取

$ $ \压裂{dS (t)} {dt} = - \压裂{\β(t)我(t) S (t)} {N} $ $
（12）
$ $ \压裂{dI (t)} {dt} = \压裂{\β(t)我(t) S (t)} {N} - \γ(t)我(t) $ $
（13）
$ $ \压裂{(t)博士}{dt} = \γ(t)我(t) $ $
(14）

在哪里\β(t) (\ \)而且\γ(t) (\ \)是随时间变化的函数\ \ (t)作为一个自变量而不是常数。由于在COVID-19感染预防和控制方面采取了政府行动，以及人们对COVID-19的认识，\β(t) (\ \)而且\γ(t) (\ \)实时变化。为了度量这种变化，将时间序列数据集划分为大小为W的时间窗口，然后以时间窗口内的最优参数解作为评价值。获取当时的历史数据\ \ (t)时，其时间窗口为\(\{{w}_{t}，0\le \mathrm{t}\le \mathrm{t} -1\}\)时，可得如下式:

$ $ \β\离开(t \右)=选择\ \{{\β}_ {{w} _ {t}} \右\},{w} _ {t}左= \[线性调频+ 1,t \] $ $
(15）
$ $ \ upgamma \离开(t \右)=选择\ \ {{\ upgamma} _ {{w} _ {t}} \右\},{w} _ {t}左= \[线性调频+ 1,t \] $ $
（16）

其中,\({\β}_ {{w} _ {t}} \)而且\ ({\ upgamma} _ {{w} _ {t}} \)表示SIR模型中某一参数解\ \ (t)在历史数据中，时间窗口大小为\ (w \)．才能得到最优解\(左选择\ \{{\β}_ {{w} _ {t}} \右\}\)在时间窗口下\ (w \)，通过搜索计算分为两个步骤:首先确定模型参数的初值，然后对模型参数进行遍历搜索。首先是模型参数初值的确定。在疫情的早期阶段，感染人数和治愈人数在人口中的比例可以忽略不计。我们可以考虑易受影响的人数左(t \ (S \ \) \)以及总人口\ (N \)近似相等，则微分式(2)可写成式(17)：

$ $ \压裂{dI (t)} {dt} = \离开(\β-γ\ \右)我(t) $ $
(17)

然后由上式得到模型的解析解，如Eq. (18)：

左(t $ $我\ \右)= {e} ^{\离开(\β-γ\ \右)t} $ $
（18)

其中，感染者人数是一个随时间变化的指数函数，然后用最小二乘法对疫情的实际数据进行回顾性拟合，得到初始值\({\β}_ {0}\)而且\({\伽马}_ {0}\)参数的。得到的初始值可以评价疫情早期的特征，但简单的指数增长模型不能完全反映疫情的全貌，需要更准确的估计。因此，基于初始值，采用COVID-19确诊病例总数和模型数值求解方法对模型参数进行遍历。

给定给定时间窗口内的数据C \ \(左\ \{左(t \右)R \离开(t \右),D \离开(t \右),0 \ t \ le t - 1 \ \} \)（\ \ (C (t \右),R左(t \) \ \)而且左(t \ (D \ \) \)分别为每日累计确诊病例数、每日累计治愈病例数、每日累计死亡病例数)，式(19)用于计算实际的每日感染人数我(t) \ \ ()：

左(t $ $我\ \右)= C \左(t \右)- r \左(t \右)- d (t) $ $
(19)

在得到每日实际感染人数后，我们用RK4方法求出模型的数值解，即预测感染人数左(t \(我\ \)\)．为了求出参数β\ (\ \)而且\γ(\ \)时，用下式计算预测结果的MSE(均方误差):

$ $ MSE \离开(\β\伽马\右)= \压裂{1}{T} \ sum_ {T} ^ {T} {(\ widehat{我}\左(T \右)- I \左(T \右))}^ {2}$ $
(20)

为了得到最优的时间窗口大小，将时间窗口大小设置为3 ~ 30进行测试，利用累计预测误差来评估每个时间窗口下预测的准确性和有效性。\({错误}_ {w} \)累积的预测误差是否在时间窗口下\ (w \)，方程如下:

$ ${错误}_ {w} = \压裂{1}{线性调频}\ sum_ {t = w1} ^ {t} \压裂{\左| \ widehat{我}\左(t \右)- I \左右(t \) \ |}{我\离开(t \右)}$ $
(21）

在模型参数的搜索过程中，如果采用网格搜索，耗时太长，容易陷入局部最优。为了克服这一问题，本文采用了一种优化的搜索方法。首先，我们假设的值β\ (\ \)大于的值\γ(\ \)在疫情的早期阶段，因为这是确保疫情继续感染的必要条件29的值R \ ({} _ {0} \)大于1并估计初始参数值\({\β}_ {0}\)而且\({\伽马}_ {0}\)用方程式。（17)及(18)．基于初始值\({\β}_ {0}\)而且\({\伽马}_ {0}\)，我们设置搜索步长和搜索间隔的大小。然后用RK4利用Eq. (6)．最后是MSE\({\β}_ {{w} _ {t}} \)而且\({\伽马}_ {{w} _ {t}} \)计算和\({\β}_ {{w} _ {t}} \)而且\({\伽马}_ {{w} _ {t}} \)以最小均方误差为最优参数。基于时间窗的参数求值的具体步骤如算法1所示。

图一个

在得到\(β\ \离开(t \) \伽马左(t \) \ \{\β\离开(t \) \伽马\离开(t \右)w1 \ t le t - 1 \ \} \)，利用机器学习方法可以预测感染系数和治愈系数的时间变化，预测疫情未来的发展趋势。

参数预测

参数预测是根据前一部分参数评估得到的模型参数随时间的变化情况，预测后续的模型参数。本节将应用机器学习中广泛使用的多项式回归算法进行跟踪和预测\(β\ \左(t \) \)而且\ \(伽马左(t \) \ \)．很难准确地直接预测\(β\ \左(t \) \)而且\ \(伽马左(t \) \ \)因为价值波动。因此，本文提出了一种新的预测方法，利用预测的方法R \ ({} _ {0} \)呈指数增长\ (\ mathrm{前任}\左(t \) \)计算它们，它们的变化曲线在疫情发展中更容易预测。基本复制数R \ ({} _ {0} \ mathrm也{}\)反映了疫情的发展。它也可以看作是一个随时间变化的函数R \({} _{0} \左(t \) \)，可由式(22)：

$ $ {R} _{0} \左(t \右)= \压裂{\β\离开(t \右)}{\伽马\离开(t \右)}$ $
(22)

为了得到\(β\ \左(t \) \)而且\ \(伽马左(t \) \ \)，我们定义了一个指数增长率指数\ (\ mathrm{前任}\左(t \) \)根据式的指数增长模型(18)，即如下式所示:

$ $ \交货左(t \右)β= \ \左(t \) \伽马\ (t \右)$ $
(23）

预测的基本繁殖数在哪里\ (\ widehat {{R} _ {0}} (t) \)，预测的指数增长率为\ (\ widehat {\ mathrm{前任}}(t) \)．通过多项式回归，可以写成如下形式:

$ ${对齐}\ \开始widehat {{R_{0}}} \离开(t \右)& =现代{0}+现代{1}R_{0} \离开({{\文本{t}} - 1} \右)+现代{2}\离开({R_{0} \离开({{\文本{t}} - 1} \右)}\右)^ {2}+ \ cdots + ~现代{n} \离开({R_{0} \离开({{\文本{t}} - 1} \右)}\右)^ {n } \\ & = \ mathop \总和\ limits_ {{i = 0}} ^ {n}现代{我}\离开({R_{0} \离开({{\文本{t}} - 1} \右)}\右)^{我}\ \ \{对齐}$ $
(24）
$ ${对齐}\ \开始widehat{{{\文本{前任}}}}\离开(t \右)& = b_ {0} + b_{1}{\文本{前任}}\离开({{\文本{t}} - 1} \右)+ b_{2} \离开({{\文本{前任}}\离开({{\文本{t}} - 1} \右)}\右)^ {2}+ \ cdots +{~}}{\文本b_ {m} \离开({{\文本{前任}}\离开({{\文本{t}} - 1} \右)}\右)^ {m } \\ & = \ mathop \总和\ limits_ {{j = 0}} ^ {m}现代{j} \离开({{\文本{前任}}\离开({{\文本{t}} - 1} \右)}\右)^ {j} \ \ \{对齐}$ $
(25）

N和m是\ (\ widehat {{R} _{0}} \左(t \) \)而且\ (\ widehat {\ mathrm{前任}}\左(t \) \)多项式(n, m≥2)，\({a}_{i} (i=\ mathm {0,1}，\dots,n)\)而且\({b}_{j} (j=\mathrm{0,1}，\dots,m)\)是这两个多项式函数的系数。为了确定多项式函数的系数和阶数，应用最广泛的最小二乘法(OLS)来评价预测结果。同时，为了保证模型欠拟合，反映疫情的实时变化，采用上节所述的时间窗口方法，解决了以下优化问题:

$ $ \ mathrm{分钟}\ sum_ {t =线性调频}^ {t - 1} {(\ widehat {{R} _{0}} \离开(t \右)——{R} _{0} \离开(\ mathrm {t} \右))}^ {2}$ $
（26)
$ $ \ mathrm{分钟}\ sum_ {t =线性调频}^ {t - 1} {(\ widehat {\ mathrm{前任}}\左(t \) \ mathrm{前任}\离开(\ mathrm {t} \右))}^ {2}$ $
(27）

W是时间窗口的大小。通过求解目标优化函数，可以得到多项式的系数和阶数，如\ ({} _ {}, i = \ mathrm{0,1}, \点,n \),\ ({b} _ {j}, j = \ mathrm{0,1}, \点,m \)．得到这些系数后，\ (\ widehat {{R} _ {0}} (t) \)而且\ (\ widehat {\ mathrm{前任}}(t) \)在时间\ (t = t \)可通过公式获得。（24，25)，然后是预测的感染率左(\ \ (\ upbeta \ mathrm {t} \) \)以及预测的恢复速度\ \(伽马左(t \) \ \)可以用公式计算。（28)及(29),即:

$ $ \ widehat{β\}\左(t \右)= \压裂{\ widehat {\ mathrm{前任}}(t) \ widehat {{R} _ {0}} (t)} {1 - \ widehat {{R} _ {0}} (t)} $ $
(28)
$ $ \ widehat{\伽马}\左(t \右)= \压裂{\ widehat {\ mathrm{前任}}(t)} {1 - \ widehat {{R} _ {0}} (t)} $ $
(29)

现在我们有了\ (\ widehat{\β}(t) \)而且\ (\ widehat{\伽马}(t) \)，然后通过模型求解法在“模型求解”中求得感染数\(左\ \ {\ widehat{我}\离开(t \右),t > t \ \} \)在随后的流行中是可以预测的。

数值结果

数据源

在本文中，我们收集了约翰霍普金斯大学的流行病学数据30.．项目数据可以在开源的GitHub网站上获得，项目的生命周期是连续的31．数据包括2020年1月23日至今的各国。该地区每日累计确诊病例数、累计死亡病例数、累计治愈病例数。以中国为例，Table1显示我们使用的数据的详细信息。在这篇文章中，我们使用了中国、韩国、法国、西班牙、意大利、德国和巴西七个国家的数据作为我们的数据集。此外，为了验证我们的方法适用于不同的流行病，我们还从中国卫生部网站上收集了2003年4月20日至2003年6月23日中国北京市的SARS疫情数据，数据格式与表中相同1．表格2显示了中国、韩国、法国、西班牙、意大利、德国和巴西的COVID-19数据，以及2003年北京SARS数据的时间框架。

表1中国COVID-19疫情数据。
全尺寸表
表2数据集描述。
全尺寸表

参数设置

  1. (1)

    窗口值的确定\ (W \)

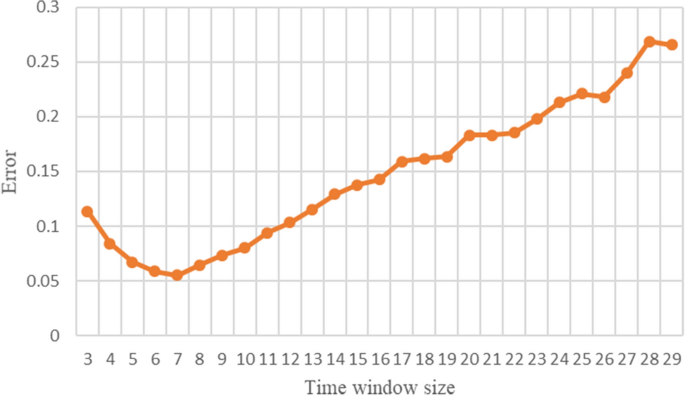
    实验中使用了不同的时间窗口大小，范围为3 ~ 30。数字2为根据式计算的中国在不同时间窗口下的累计预测误差(21)．可以发现，存在一个使累积预测误差最小的时间窗口，即\(w = 7\)．

    对于数据集中的每个国家，各自的最佳时间窗口大小如表所示3.．

  2. （2）

    参数评估

    在确定合适的时间窗大小后，使用算法1对模型参数进行评估。采用多项式回归预测参数时\(β\ \左(t \) \)而且\ \(伽马左(t \) \ \)时，设多项式的初阶为2，即，\ (n = m = 2 \)．因为\(β\ \左(t \) \)而且\ \(伽马左(t \) \ \)为非负的，如果在回归计算中它们的值小于0，则置其为0。模型求解过程中的停止条件为le 0 \(我(t) \ \)．最后，运用模型求解方法对疫情发展趋势进行预测。

    图2
    图2

    当时间窗口大小为3-29时预测误差的变化。

    全尺寸图像
    表3数据集中各个国家或地区的最佳时间窗口大小。
    全尺寸表

实验及结果分析

为了说明TW-SIR模型的科学性和有效性，我们将在本节中提出并分析三个研究问题(RQ1, RQ2和RQ3)。

RQ1实验结果

在流行病模型中，一个非常重要的问题是流行病何时结束。要回答这个问题，一个常用的指标是基本繁殖数R \ ({} _ {0} \)这被定义为一个感染者在康复之前将疾病传播给其他多少人的平均值。在TW-SIR预测模型中，R \({} _{0} \左(t \) \)是一个随时间变化的函数。如果R \({} _{0} \离开(t \右)> 1 \)，这种流行病将迅速传播，并感染总人口的一定比例R \({} _{0} \离开(t \右)< 1 \)在美国，疫情最终将得到控制和结束。因此，通过观察的变化R \({} _{0} \左(t \) \)预测未来\ (\ widehat {{R} _{0}} \左(t \) \)，可以了解疫情的发展趋势以及疫情的控制措施是否有效。同时，本文还提出了指数增长率指标\(前左(t \) \ \)是用的，也就是区别吗\(β\ \左(t \) \)而且\ \(伽马左(t \) \ \)，来衡量疫情的指数增长趋势，这也反映了疫情的变化趋势。当\ (\ mathrm{}交货(\ mathrm {t}) > 0 \)，这意味着传染病的感染速度快于治愈的速度。相反，受疫情感染的人数正在逐渐治愈，疫情正在逐渐结束。首先，我们将TW-SIR模型应用于中国、韩国、意大利、西班牙、巴西、德国和法国2020年1月27日至7月2日的COVID-19历史数据进行测量R \({} _{0} \左(t \) \)而且\(前左(t \) \ \)．文中将TW-SIR预测模型与基于公式推导的测量方法进行了比较22．表4而且5，分别总结出基本复制数R \ ({} _ {0} \)呈指数增长\(\)交货采用TW-SIR模型和文献中采用的公式推导方法进行测量22．从表中可以看出，基于TW-SIR模型测得的参数值更接近实际情况，而公式推导法存在过大或过小等与实际情况不一致的异常值。

表4根据TW-SIR模型对繁殖数和指数增长率的测量。
全尺寸表
表5根据公式推导法测定繁殖数和指数增长率。
全尺寸表

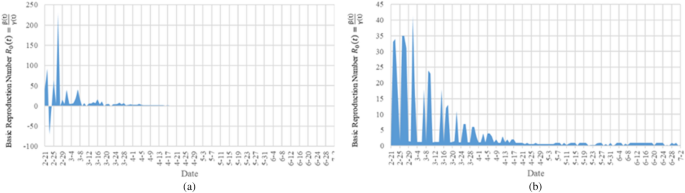
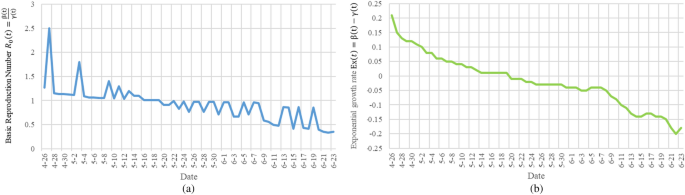
数字3.A是使用数据进行测量的结果R \({} _{0} \左(t \) \)文献方法22和无花果。3.b为采用TW-SIR模型测量的结果R \({} _{0} \离开(\ mathrm {t} \) \)．所有日期从2020年2月21日起以两位数计算。R \({} _{0} \离开(\ mathrm {t} \) \)在无花果。3.A已经达到200，并且有负值，这显然是不正确的。我们也可以从图中看到。3.B表示的值R \({} _{0} \离开(\ mathrm {t} \) \)更小，更符合实际情况。此外，在图。3.B、可以看出有一个转折点R \({} _{0} \离开(\ mathrm {t} \右)< 1 \)2020年4月19日，即意大利疫情达到高峰。2020年4月19日之后，R \({} _{0} \离开(\ mathrm {t} \) \)保持在低于1的水平，这意味着感染人数我(t) \ \ ()将会减少，并最终终结意大利的疫情。TW-SIR模型可以准确测量时间R \({} _{0} \离开(\ mathrm {t} \右)< 1 \)测量值与实际情况较为接近。同时，我们的结果与大多数文献中测量的结果相似32，表明了TW-SIR模型测量的有效性R \({} _{0} \离开(\ mathrm {t} \) \)．

图3
图3

基本繁殖数R \({} _{0} \离开(\ mathrm {t} \) \)在意大利。

全尺寸图像

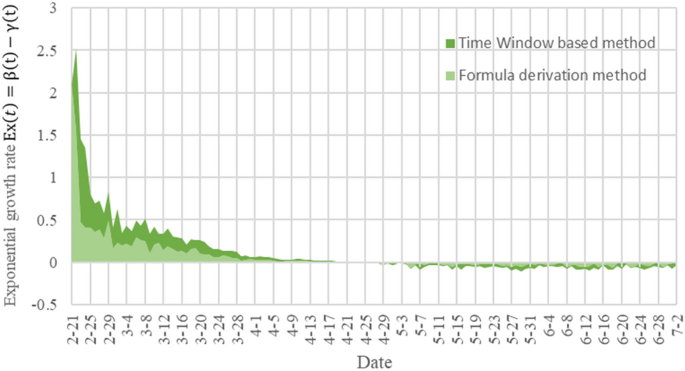
同样,无花果。4给出了用TW-SIR模型和公式推导法测量指数增长率的结果\ \ (Ex (t))．指数级增长率\ \ (Ex (t))两种方法计算出的结果都能反映疫情的发展变化，且总体趋势大致一致，都能测算出疫情的高峰时间。然而,\ \ (Ex (t))基于TW-SIR模型计算的值包含了基于公式推导法计算的值，可以更清晰地反映指数增长率的变化。

图4
图4

指数增长的结果\ \ (Ex (t))2020年2月21日至7月2日在意大利举行。(深绿色曲线为我们提出的TW-SIR预测模型的测量结果，浅绿色曲线为本文中采用的基于公式的方法22)．

全尺寸图像

RQ2实验结果

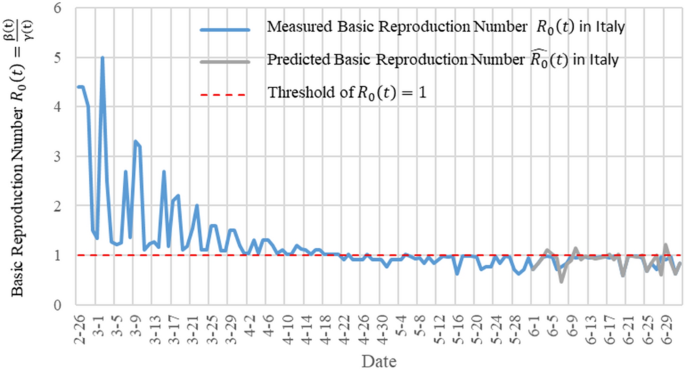
数字5显示了测量结果R \({} _{0} \离开(\ mathrm {t} \) \)预测结果\ (\ widehat {{R} _{0}} \左(t \) \)在意大利采用TW-SIR模型。蓝色曲线是被测量的R \({} _{0} \离开(\ mathrm {t} \) \)， 2020年2月26日至7月2日。灰色曲线是预测值\ (\ widehat {{R} _{0}} \左(t \) \)2020年6月1日至7月2日。红色虚线是表示的阈值\ (\ widehat {{R} _{0}} \离开(t \右)= 1 \)．我们可以看到R \ ({} _ {0} \)在意大利几乎是一样的R \ ({} _ {0} \)在中国疫情的早期阶段。从图中可以看出R \ ({} _ {0} \)4月19日左右是疫情高峰的转折点。与中国相比，意大利进入高峰的时间相对较长，这可能是由于防控策略不同造成的。

图5
图5

R \({} _{0} \离开(\ mathrm {t} \) \)预测结果\ (\ widehat {{R} _{0}} \左(t \) \)由TW-SIR预测模型测量。

全尺寸图像

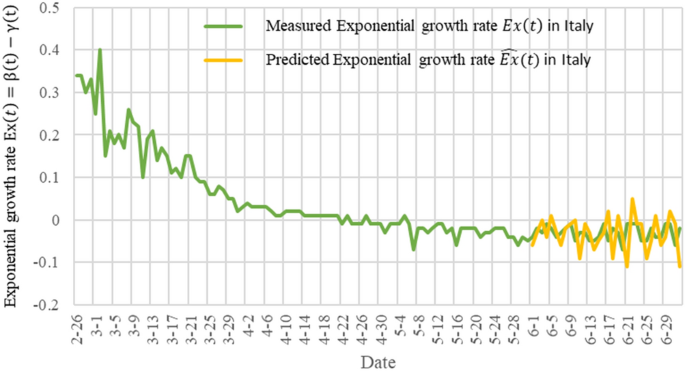
在无花果。6，我们显示了指数增长速度\ \ (Ex (t))以意大利和预测的指数增长率来衡量\ (\ widehat {\ mathrm{前任}}(t) \)．绿色曲线是测量的指数增长率\ \ (Ex (t))， 2020年2月26日至7月2日。黄色曲线是预测的指数增长率\ (\ widehat{}交货(t) \)2020年6月1日至7月2日。在无花果。6在美国，意大利疫情的指数增长率已接近零。如果这种情况持续下去，受感染人数将会减少，这种流行病将会消失。但由于气温的变化、政府的防控措施和人们的意识，从2020年8月开始，又出现了第二波感染，我们后面会讨论。数据5而且6表明TW-SIR模型准确预测了的变化\ (\ widehat {{R} _{0}} \左(t \) \)而且\ (\ widehat {\ mathrm{前任}}(t) \)，说明我们的参数预测方法是有效的。

图6
图6

感染的基本数量\ \ (Ex (t))以及预测的基本感染数量\ (\ widehat{}交货(t) \)采用TW-SIR预测模型对意大利的新冠肺炎疫情进行了预测。

全尺寸图像

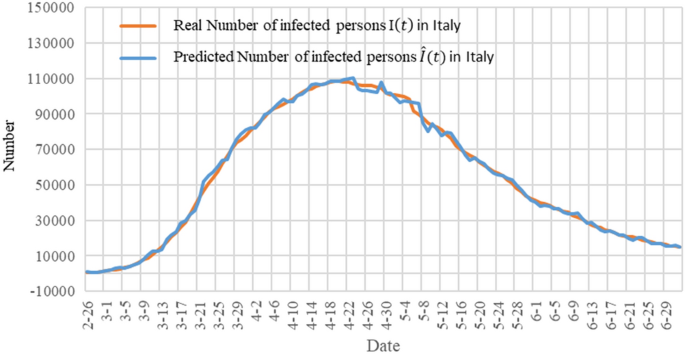
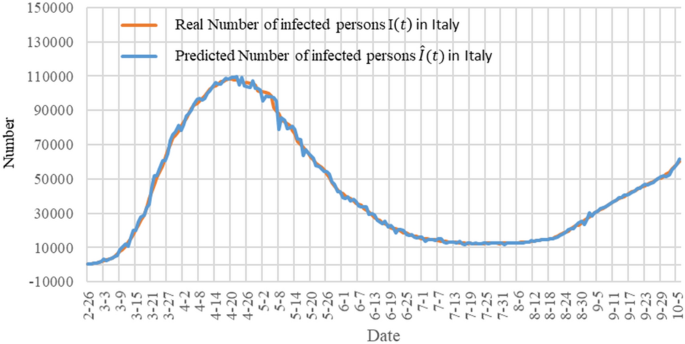
为了显示我们模型的准确性，我们在图中显示了我们的模型对第二天(单日预测)的预测结果。7．图中的橙色曲线表示实际感染人数我(t) \ \ ()在意大利，蓝色曲线代表预测的感染人数\ (\ widehat{我}(t) \)．从图中可以看出，预测曲线与实际数据曲线非常接近。

图7
图7

意大利单日感染人数预测。橙色曲线代表实际感染人数我(t) \ \ ()在意大利，蓝色曲线代表预测的感染人数\ (\ widehat{我}(t) \)．

全尺寸图像

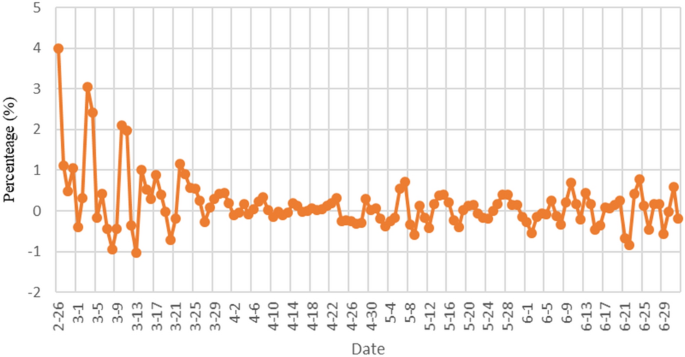
我们进一步检验了我们预测的准确性，计算了单日预测感染人数的误差，如图所示。8．预测感染人数的错误率都在5%以内，说明我们的模型可以准确预测第二天的感染人数。

图8
图8

意大利单日感染人数预测的预测误差。

全尺寸图像

从将TW-SIR模型应用于中国和意大利的疫情数据的结果来看，该模型可以有效地测量疫情发展过程中参数的实时变化，包括疫情的基本再现数和疫情发展的指数增长速度，以及疫情跟踪和预测的发展趋势。

RQ3实验结果

从2020年9月到秋冬季节，许多国家出现了第二波COVID-19感染。我们将TW-SIR模型应用于数据集中7个国家2020年8 - 10月的数据，测量结果如表所示6．

表6根据TW-SIR模型对繁殖数和指数增长率的测量。
全尺寸表

在韩国和巴西R \ ({} _ {0} \)值小于1，说明9 - 10月感染人数呈下降趋势。对于指数增长速度，只有中国和韩国的指数增长速度小于0，平均感染人数我(t) \ \ ()在这两个国家都很小，这意味着这两个国家的疫情发展趋势在很长一段时间内处于相对稳定的状态。意大利、西班牙、德国和巴西都出现了第二波攻击，病例数量正在上升。

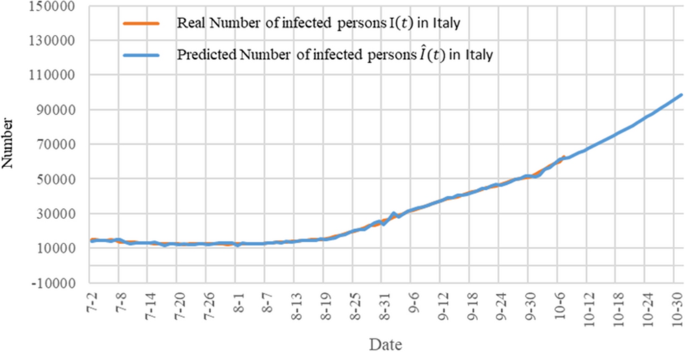
例如，在意大利，无花果。9为应用TW-SIR模型后现有感染数量的趋势变化。橙色的线是实际感染人数，蓝色的线是预测感染人数的变化。从图中可以看出，2020年7月至8月初，现有感染人数呈缓慢下降趋势。的平均值R \ ({} _ {0} \)利用TW-SIR模型得到的该时段感染人数为0.333，而从8月开始感染人数逐渐增加，平均值为R \ ({} _ {0} \)1.551。TW-SIR模型成功预测了第二波感染趋势。

图9
图9

2020年2月至10月意大利单日感染人数预测。

全尺寸图像

从7月至10月意大利的感染人数趋势来看，第二波感染人数有所增加。后端的蓝线是TW-SIR预测曲线(图2)。10)．

图10
图10

2020年10月起意大利感染人数预测。

全尺寸图像

讨论

新冠肺炎疫情自中国暴发以来，已蔓延到全球多个国家和地区。截至2020年10月11日，全球已有188个国家和地区确诊病例37213592例。不同国家和地区采取了不同的防控措施，如关闭城市、关闭学校、居家隔离等。结果，这一流行病在不同程度上发展。在以往的研究中，流行病传播模型通常采用常数来测量参数1，33，34，35但很难衡量疫情的动态和实时演变。与传统SIR模型的固定参数不同，我们利用时间窗对模型参数进行动态测量，提出了基于时间窗的TW-SIR模型。TW-SIR模型的优点是更符合实际疫情参数的动态测量。我们将提出的TW-SIR模型应用于2020年1月27日至7月2日中国、韩国、意大利、西班牙、巴西、德国和法国的历史数据，以衡量基本感染人数R \ ({} _ {0} (t) \)还有指数增长速度\ \ (Ex (t))．与文献中提出的公式测量方法进行了比较22， TW-SIR模型的测量结果更接近实际情况。

至于R \ ({} _ {0} \)评估值，见表6在美国，巴西是最高的R \ ({} _ {0} \)平均(5.136)，中国最低R \ ({} _ {0} \)7个国家的平均值(2.285)。刘颖等对R \ ({} _ {0} \)在12项研究中发现，估计的平均水平R \ ({} _ {0} \)平均为3.28，中位数为2.79,IQR为1.1632．我们的R \ ({} _ {0} \)七个国家的平均测量结果为平均R \ ({} _ {0} \)值为3.656，与有研究发现的值得指出的测量值相似R \ ({} _ {0} \)较大，这是因为我们只选取了参数测量，7个国家的covid - 19疫情在各个国家的传播存在差异，还需要进一步的研究来证实这一测量指标的增长也说明了一些问题，在选取的7个国家中，只有中国的指数增长率为负，对于其他国家的疫情发展程度并没有达到一个相当低的水平。这也说明中国在疫情防控方面做得很好。

为了证明我们的方法适用于不同的流行病，我们还使用了2003年4月20日至2003年6月23日中国北京SARS的流行病学数据。数字11的变化曲线R \ ({} _ {0} \)呈指数增长\(\)交货2003年在中国北京爆发的非典其中，北京市SARS传播基础感染病例数平均为2.099例，平均指数增长率为−0.02046例。与新冠肺炎在中国的传播相比，R \ ({} _ {0} \)SARS感染初期的死亡率约为一半R \ ({} _ {0} \)其指数增长速度约为COVID-19的四分之一。这是符合实际情况的32这表明新冠肺炎的传播比2003年的SARS更为猛烈。同时，整个疫情期间的平均指数增长率为负，确保了SARS疫情的结束。

图11
图11

R \({} _{0} \离开(\ mathrm {t} \) \)而且\ (\ mathrm{前任}\离开(\ mathrm {t} \) \)2003年在中国北京爆发的非典

全尺寸图像

我们的模型在流行病传播过程的参数测量和趋势预测方面存在一些局限性。首先，该模型没有考虑无症状感染者，因为他们很难获得，而且可能不准确。其次，我们研究的另一个局限性是，我们在模型的每个部分使用的方法可能不是最优的，有更好的方法来求解模型和预测参数。

结论

随着其他国家和地区疫情暴发，新冠肺炎疫情已席卷全球。在本研究中，我们提出了一个TW-SIR预测模型，该模型能够反映不同地区、不同政策、不同流行病在感染过程中的实时趋势。应用机器学习方法预测感染的基本数量R \ ({} _ {0} \)以及传染病的指数级增长速度\(\)交货．我们对COVID-19进行了数学和数值分析。数值计算结果表明，该模型能有效测量传染病传播过程中各参数的实时变化，包括基本感染数R \({} _{0} \离开(\ mathrm {t} \) \)呈指数增长\ \ (Ex (t))．预测单日新冠肺炎感染人数的错误率在5%以内。总的来说，这些参数的测量对于了解COVID-19的传播情况，指导制定控制策略和措施具有重要意义。

此外，从2020年9月到秋冬季，许多国家出现了第二波COVID-19感染。从我们对2020年7月至10月意大利疫情数据的分析中，我们发现TW-SIR模型可以适用于COVID-19的第二个高峰。就我们衡量的参数而言，中国和韩国一直保持在较低水平R \ ({} _ {0} \)而意大利、西班牙、巴西、德国和法国大多仍在增长。这意味着疫情防控措施需要更加严格，确保疫情不失控。

最后，基于实验结果，TW-SIR模型也可以应用于不同的流行病，如SARS。虽然我们对无症状感染者的数据缺乏了解，但我们的研究结果将为后续的疫情防控提供一些建议。