介绍

在本文中,我们提出一个现象学模型预测的死亡和住院的人在一个大流行浪潮,假设线性依赖的,死亡的人数有一定延迟\ \(τ)> 0 \)新病例的数量,同样的,住院的数量线性依赖于新病例的数量与另一个延迟δ> 0 \ \ (\)。预测进行每天使用日常数据在新情况下,死亡和住院的流行浪潮的开始。实现这个想法是这样的:首先,某一天T在大流行期间,使用新病例累积数据,日期,确定新病例的增长模式功能φ\ (\ \)。然后定义死亡的模型函数根据线性函数\ (t \ mapsto \φ”(t - \τ)\),在那里\ \(τ\)延迟是事先不知道。以这种方式定义的参数模型的函数确定的最小二乘(LS)问题上的数据的死亡。死亡的预测数字现在可以了\ \(τ^ \ \)明星天从那一天开始\ (T + 1 \),在那里\ \(τ^ \ \)明星参数的最优LS-value吗\ \(τ\)。我们以类似的方式定义的模型函数线性依赖于函数住院\ (t \ mapsto \φδ)(t - \ \),在那里\三角洲(\ \)延迟是事先不知道。重复这个过程对于死者,住院的预估数字是下一个\(δ^ \ \ * \)天。

将该方法应用于COVID-19的第三波大流行在克罗地亚显示,它是可以接受的死亡人数的预测,在接下来的10到12天,平均死亡率有关\ (1.8 \ % \)。也可以预测数字的住院一段时间包括减少数量的新病例的开始,在接下来的11天,早些时候,在进步的新病例的数量的增长,相当长时间。

当大流行刹车估计是一个至关重要的问题,尽快的进步的感染,已故,住院,恢复情况。COVID-19流行病爆发以来,已经有大量的出版物提出,基于可用的数据,不同的数学模型对短期和长期预测,以便卫生当局可以计划和资源来对抗流感大流行做好准备。

COVID-19数学模型(和其他流行或大流行)可以分为1,2:(1)传播动力学模型,和(2)现象学模型。的主要目的传播动力学模型3,4,5,6,7,8,9流行病是描述机制和理解其行为以及人类干预的影响。另一方面现象学模型2,10,11不针对流行病理解机制,但可用于高效和快速的预测。

上下文中的现象学COVID-19流行病模型,提出:一个数学模型估算病死率风险,即死于某种疾病的比例相比,人被诊断出患有这种疾病的总数为一个特定的时期12;一个数学模型来确定最大允许每日增长偏离指数增加稳定和数量下降13;一个方法来预测死亡的人数14。在裁判。15基于数据的第一波COVID-19大流行在美国(美国)和欧洲经济区国家(EEA),提出了一种使用高斯模型函数数学模型预测的必要能力的医院在美国和欧洲经济区。在裁判。16设计一个框架来评估COVID-19死亡率预测的预测效度。作者在裁判。17研究与观察到的趋势相关联的因素在住院期间死亡率在美国的前九个月COVID-19大流行。

尤其是在文献中常用的逻辑增长模型及其推广10,11,18,19,20.。例如,在裁判。20.分析了增长排名前25位的行为受影响最严重的国家通过当地的斜率分析和确定了三种不同的模式,各个国家根据严格的控制协议:兴衰,幂律和物流。此外,在裁判。11作者提出了一种新的物流模式,非常适合幂律流行的增长。结果表明,此模型始终使峰值高度准确的预测,峰值位置和累积饱和值不完整的流行增长曲线。

我们的纸是组织如下。在下一节中,我们提出一种新的预测方法,在大流行期间,住院和死亡的数量根据新病例的数量。在“COVID-19流行的应用方法“我们应用该方法在克罗地亚COVID-19大流行的第三次浪潮。一些结论给出了”结论”,在“数据和计算机代码的可用性“我们描述我们的方法开发的免费软件。

预测的死亡人数和人员住院

假设在流行病我们手头的数据\ ((t_i、n_i d_i h_i) \),\ (i = 1, \点,m \)确认新病例的数量\ ((n_i) \),新已故\ ((d1) \),总数量的人住院\ ((h_i) \)天\ (t_{我}\识别)一定的观察期间\ ([t_1、t_m] \)。

假设已故的数量t取决于在某个前一天新病例的数量\ (t - \τ\),\ \(τ)> 0 \),新住院的数量t取决于前一天新病例的数量\ (t -δ\ \),δ> 0 \ \ (\),我们将努力估计死亡的数量在即将到来的时期\ ([t_m t_m + \τ]\)在即将到来的时期,住院\(δ)[t_m t_m + \ \),从而使监控和应对流感大流行的重要指标。

为了实施这些假设使用可用的数据,我们将首先确定相应的增长模式功能φ\ (\ \)为新报告病例。

由于不同的方法和动态的日常测试整个星期,《每日新病例的数据是不可靠的(即包含一些随机误差)。因此,而不是使用每日数据,我们将估计参数的值一个,b,c增长模式的功能φ\ (\ \)基于累积数字\ (N_i = \ \长成具和_ {s = 1} ^我n_s \),\ (i = 1, \点,m \),同期的新病例\ ([t_1、t_m] \)。导数\ (t \ mapsto \φ”(t) \)将被用作模型函数每天新病例的时期\ ([t_1、t_m] \)。

增长模式的功能φ\ (\ \)可以选择任何一个著名的增长模式功能:物流或广义物流模式函数(见例如参考文献。21,22),龚帕兹模型函数(见例如Ref。23),或Weibul模型函数(见例如Ref。24)。根据建模大量引用COVID-19大流行(见例如参考文献。11,19,20.),在本文中,我们将使用普通的物流模型函数

$ ${对齐}\ \开始φ(t): = y (t, a, b, c) = \压裂{一}{1 + b \ e ^ {- ct}}, \四a, b, c > 0 \{对齐}$ $
(1)

微分方程的解是什么

$ $ \{对齐}开始y ' y = c \ \, (y) \四,c > 0, \{对齐}$ $
(2)

描述以下法律:病例数的增长率t t成比例的病例总数在那一刻,y(t),和潜在的新病例的数量,\ ((y (t)) \)。

未知的参数一个,b,c将取决于解决非线性最小二乘问题25,26

$ ${对齐}\ \开始mathop {\ mathrm {argmin}} \长成具\限制_ {a, b, c > 0} \ \和限制_ {i = 1} ^ m (N_i-y (t_i; a, b, c)) ^ 2。\{对齐}$ $
(3)

获得的参数表示\(一颗^ \ \),\ (^ \ b星\),\(恒星c ^ \ \),并且模型的功能φ\ (\ \)将函数\ (t \ mapsto y (t; ^ \明星,b ^ \恒星,恒星c ^ \) \)。

简单的全局优化问题(共和党)(3)可以解决使用Mathematica模块NonlinearModelFit27。

预测死亡的数量

我们已经说过,已故的数量的依赖新病例的数量是基于以下假设:

  1. (我)

    有一个时间延迟\ \(τ\)感染和死亡之间;

  2. (2)

    已故的数量线性依赖于导数\ \(φ”(t - \τ;^ \明星,b ^ \明星,c ^ \明星)\),在那里\(一颗^ \ \),\ (^ \ b星\),\(恒星c ^ \ \)通过求解最优参数的非线性最小二乘问题(3)的基础上累积数据\ ((t_i、N_i) \),\ (i = 1, \点,m \)。

知道该模型函数φ\ (\ \)累积的新病例的数量,即知道参数\ \(^ \明星,b ^ \明星\,恒星c ^ \ \)日常已故的,函数可以表达的(参也看到类似的模型。24,28,29日)

$ ${对齐}\ \开始varphi (t, u \α\τ)= u +α\ \ \φ”(t - \τ;一颗^ \ b ^ \明星,c ^ \明星)。\{对齐}$ $
(4)

的参数u,\α(\ \)和\ \(τ\)模型的函数\ \ varphi \ ()将决定使用数据\ ((t_i、d1) \),\ (i = \ kappa \点,m \)在已故的数量如下共和党(数据为死者\ (\ kappa \),说15天后,因为我们假设死亡之前,属于前面的大流行波):

$ ${对齐}\ \开始粉碎[t] {\ mathop {\ mathrm {argmin}} \长成具\限制_ {uα\ \τ> 0}F (u,α\ \τ)\ qquad F (u,α\ \τ)= \ \和限制_ {i = \ kappa} ^ m (d1 - \ varphi (t_i; u,α\ \τ))^ 2}。\{对齐}$ $
(5)

此问题的解决方案将会表示\ ((u ^ \明星\τ^ \明星,alpha ^ \ \ *) \):\ \(τ^ \ \)明星是新病例之间的平均时间(天)和相应的死亡,然后呢\恒星(alpha ^ \ \ \)代表着已故的比例在新病例报道\ \(τ^ \ \)明星天前。

因为一般来说,数量\ \(τ^ \ \)明星不会是一个整数,我们将表示{\ \(\帽子τ}= \ lfloor \τ^ \ \ rceil \星)最近的整数。因此,期间死亡的数量\ ([t_ {m + 1},识别t_m + \帽子{\τ}\]\)的\({\τ}\ \帽子)天可以使用公式计算

$ ${对齐}\总和\ \开始限制_ {t = t_m + 1} ^ {t_m + \帽子{\τ}}\ lfloor \ varphi (t, u ^ \明星\α^ \明星\τ^ \明星)\ rceil。\{对齐}$ $
(6)

这个过程应该重复,通过添加新数据,每一天。

备注1

因为数字的敏感性共和党(5),我们将解决这个问题同样在参考文献。30.,31日:首先我们使用全局优化算法确定初始近似值直接32,33,34,然后我们应用牛顿优化方法25,26通过使用Mathematica模块NonlinearModelFit。同样将解决完成共和党(9)。

预测住院的数量

之间的连接数量的住院和新感染的是已故的情况要复杂得多。也就是说,总数\ (h_i \)天的住院\ (t_i \)可以被定义为

$ $ \{对齐}开始h_i = h_张{}+ \ν_i - \ρ_i-d_i \{对齐}$ $
(7)

在哪里\ \(ν_i \)住院的人数在一天\ (t_i \),\ \(ρ_i \)天从医院发布的数量吗\ (t_i \),\ (d1 \)病人死于天的数量吗\ (t_i \)。请注意,ρ_i-d_i \ \ν_i - \ \)表示变化的增长或减少的住院病人的数量\ (t_i \)。我们将假设如下:

  1. (我)

    有一个时间延迟\三角洲(\ \)之间的新情况和新住院;

  2. (2)

    住院的数量线性依赖于导数\ \(φ”(t - \三角洲;^ \明星,b ^ \明星,c ^ \明星)\),在那里\(一颗^ \ \),\ (^ \ b星\),\(恒星c ^ \ \)通过求解最优参数的非线性最小二乘问题(3)的基础上累积数据\ ((t_i、N_i) \),\ (i = 1, \点,m \)。

基于这些假设和了解函数的增长模式\ (t \ mapsto \φ(t; ^ \明星,b ^ \恒星,恒星c ^ \) \)对于新病例的累计数量,估计可以表示为住院(参也看到类似的模型。28,29日)

$ ${对齐}\ \开始psi (t, u, v, \δ)= u + v \ \φ”(t - \三角洲;一颗^ \ b ^ \明星,c ^ \明星),\{对齐}$ $
(8)

的参数u,v,\三角洲(\ \)模型的函数\ψ(\ \)将决定使用数据\ ((t_i、h_i) \),\ (i = \ kappa \点,m \)在住院的人的数量,如下共和党:

$ ${对齐}\ \开始mathop {\ mathrm {argmin}} \长成具\限制_ {u, v,δ> 0}\ F (u, v, \δ)\ qquad F (u, v, \δ)= \ \和限制_ {i = \ kappa} ^ m (h_i \ psi (t_i; u, v, \δ))^ 2 \{对齐}$ $
(9)

的人住院数据在哪里\ (\ kappa \),说15天后,因为我们假设住院之前,属于前一波。此问题的解决方案将会表示\ ((u ^ \明星,v ^ \明星,δ^ \ \ *)\)。数量\(δ^ \ \ * \)是新病例之间的平均时间(天)和相应的住院治疗。

数量\ (h_i \)住院的一天\ (t_i \),我> m \ \ (),现在可以估计

$ ${对齐}h_i \ \开始大约u ^ \星+ v ^ \星\ \φ”(t_i -δ^ \ \明星;^ \明星,b ^ \明星,c ^ \明星)。\{对齐}$ $
(10)

比较(7)和(10),我们有

$ ${对齐}\ \开始ν_i - \ρ_i-d_i \大约v ^ \明星\φ”(t_i -δ^ \ \星)- v ^ \星\φδ^ (t_张{}-识别\ \ *)\大约v ^ \明星\ \φ”(t_i -δ^ \ \明星)= \ psi ' (t_i u ^ \明星,v ^ \明星,δ^ \ \明星)。\{对齐}$ $
(11)

因此,变化的增长或减少ρ_i-d_i \ \ν_i - \ \)住院的患者数量的一天\ (t_i \),我> m \ \ (),可以表示为价值\(\ψ”(t_i u ^ \明星,v ^ \明星,δ^ \ \ *)\)。

重要的点的函数\ψ(\ \)是它的最大米这是达成的

$ $ \{对齐}开始t_M =δ^ \ \明星+ \ tfrac {\ ln (b ^ \星(2 - \ sqrt {3}))} {c ^ \明星}\{对齐}$ $
(12)

和它的零\ \ (T_0 = (T_0,0))。人能说住院的人数进步成长直到那一刻\ (t_M \)和一个递减的增长之后,和住院的数量减少\ (t_0 \)。

因为一般来说,数量\(δ^ \ \ * \)我们不是一个整数,将表示吗\(\帽子{\三角洲}=δ^ \ lfloor \ \ * \ rceil \)最近的整数。因此,未来期间住院的预测数字\(\帽子δ}{\ \)天是

$ ${对齐}\ lfloor \ \开始psi (t_m + 1; u ^ \明星,v ^ \明星,δ^ \ \ *)\ rceil \; \点\;\ lfloor \ psi (t_m +δ}{\ \帽子;u ^ \明星,v ^ \明星,δ^ \ \ *)\ rceil。\{对齐}$ $
(13)

这个过程应该重复,通过添加新数据,每一天。

我们也该方法开发的软件支持的形式Mathematica模块,看到“数据和计算机代码的可用性”。

COVID-19流行的应用方法

我们将测试方法对数据在克罗地亚COVID-19大流行的第三次浪潮,预测的住院人数和死去的人。

COVID-19流行在克罗地亚

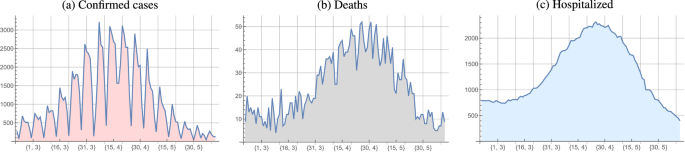
我们将使用每日新病例(图上的数据。1(图一),死亡。1b),和住院(无花果。1c)在克罗地亚,可用https://covid.ourworldindata.org/data/owid-covid-data.xlsx从2月20日开始,2021年宣布大流行在克罗地亚的第三次浪潮。这是第一天,不多了\ (t_1 = 1 \)。6月7日将被视为大流行波的最后一天。

图1
图1

每日新病例的数量,2021年2月20日以来的死亡和住院。

全尺寸图像

因为我们认为已故的数量和住院的落后好几天新病例的数量,我们会考虑新病例的数据从2月20日开始,2021年,和死亡和住院数据从3月8日开始,2021年,即15天后,认定之间的死亡和住院日期仍与前一波大流行。

模型是构思,这样我们每天查看当前数据,根据这些数据估计死亡和住院的可能的未来的数字。

让\ ((t_i、n_i d_i h_i) \),\ (i = 1, \点,m \),是大流行的数据可用\ (t_m \)。为了测试我们的方法,我们将这些数据分为两个部分:训练数据\ ((t_i、n_i d_i h_i) \),\ (i = 1, \点,T \),测试数据\ ((t_i、n_i d_i h_i) \),\ (i = T + 1 \点,m \)。训练数据将被用来估计最优参数,和测试数据来评估我们的方法的准确性。

预测死亡的数量

使用我们的数据,结果表明已故的估计数字\ ([T, T + \帽子{\τ}\]\)密切关注实际死亡人数几乎所有的数量\ (T > 50 \)。使用提供的相关的计算软件(参见“数据和计算机代码的可用性”)是为每一个在[75]\ (T \ \)(4月10日到5月5日),平均延迟\({\τ}\ \帽子)对于这样的T与标准偏差1.77是12.84的,死者在新病例的比例\({\τ}\ \帽子)天前是\ (1.74 \ % \)平均标准偏差为0.08。

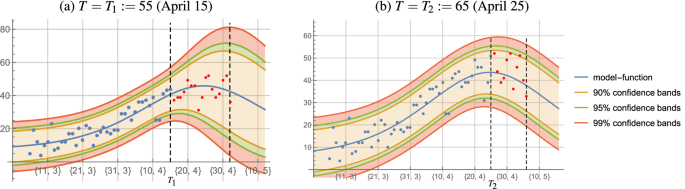
作为一个例子,我们首先考虑训练数据的逐步增长的新病例\ (T = T_1: = 55 \),即4月15日(见第一个垂直虚线在无花果。2一个)。

最优参数\(^ \明星_1,b ^ \明星_1,c ^ \明星_1)\)物流模型的函数将使用训练数据确定\ ((t_i、N_i) \),\ (i = 1, \点,T_1 \)的累积数目的新病例,而最优参数\ (u ^ \明星_1 \),\ (alpha ^ \ \明星_1 \)和\ \(τ^ \明星_1 \)定义的函数\ \ varphi \ ()由(4使用训练数据),将决定\ ((t_i、d1) \),\ (i = \ kappa \点,T_1 \)为死者在同一时期,解决共和党(5)。结果如表所示1。

使用测试数据对死者来说,相同的表显示了期间的实际死亡人数{\ \(\帽子τ}_1 = \ lfloor \τ^ \明星_1 \ rceil = 17 \)天从4月16日开始,和公式预测的数量(6)。注意,对于这个天之期预测不同小从已故的实际数量。此外,已故的比例从17天前新病例\(\α_1 ^ \明星\大约2 \ % \)(见表1)。

图2
图2

图形模型的功能\ \ varphi \ ()为适应和信心的乐队。

全尺寸图像
表1的最优物流增长模式函数的参数φ\ (\ \)和模型的功能\ \ varphi \ ()(推迟死亡的4),使用训练数据\ ((t_i、n_i d_i) \),\ (i = 1, \点,T \)与\ (T = T_1: = 55 \)和\ \ (T = T_2: = 65),比较预测的数量和实际死亡人数\ ([T, T + \帽子{\τ}\]\)。
全尺寸表

图2显示了图模型的功能\ \ varphi \ ()由(4)(蓝色曲线),函数φ\ (\ \)事先确定物流模型函数的累积数量的新病例。红点代表死亡的实际日常数据在第一次17天之后,4月15日(总共732人死亡)。可视化也是\ \ (90 \ %),\ \ (95 \ %),\ \ (99 \ %)信心乐队配合的功能\ \ varphi \ (),证明结果。垂直虚线之间的数据的范围T和\ ([T + \帽子{\τ}\]\)。

以类似的方式,我们将分析训练数据在一段时间内包括的新病例的数量开始减少\ \ (T = T_2: = 65),即4月25日(见第一个垂直虚线在无花果。2b)。最优参数\(^ \明星_2,b ^ \明星_2,c ^ \明星_2)\)物流模型的功能,在这种情况下,以及参数\ (u ^ \明星_2 \α^ \明星_2 \),\ \(τ^ \明星_2 \)相应的功能\ \ varphi \ ()也见表1。

使用测试数据对死者来说,相同的表显示了期间的实际死亡人数{\ \(\帽子τ}_2 = \ lfloor \τ^ \明星_2 \ rceil = 11 \)天从4月26日开始,和公式预测的数量(6)。此外,已故的比例从11天前新病例\(α_2 ^ \ \ * \大约1.7 \ % \)。

图2b显示了图模型的功能\ \ varphi \ (),函数φ\ (\ \)确定了。红点代表死亡的实际日常数据在第一次后11天4月25日(总共483人死亡)。可视化也是\ \ (90 \ %),\ \ (95 \ %),\ \ (99 \ %)信心乐队配合的功能\ \ varphi \ (),证明结果。

预测住院人员的数量

模型的参数函数(8)将决定基于训练数据\ ((t_i、N_i) \),\ (i = 1, T \ \点),累计数量的新病例。在那之后,最优参数\ (u ^ \明星\),\ (v ^ \星\),\(δ^ \ \ * \)模型的函数\ψ(\ \)据公式(8),将住院的数量与新病例的数量,将估计解决共和党(9)基于训练数据\ ((t_i、h_i) \),\ (i = \ kappa \点,T \)的人住院。这共和党将再次得到解决就像描述的评论吗1。用这种方法获得一个数字

$ ${对齐}\ lfloor \ \开始psi (t_ {T + 1}识别;u ^ \明星,v ^ \明星,δ^ \ \ *)\ rceil \; \点\;\ lfloor \ psi (t_ {T + \帽子{\三角洲}};u ^ \明星,v ^ \明星,δ^ \ \ *)\ rceil \{对齐}$ $

预测的数量在未来住院\(\帽子δ}{\ \)天从天\ (t_ {T + 1} \识别)。这些数据必须与实际数量同期住院。这可以通过各种措施进行比较,看到例如Ref。35,我们将使用平均绝对误差百分比(日军)。

应用上述软件,描述在“数据和计算机代码的可用性”,我们的数据在[75]\ (T \ \)(4月5日到5月5日),显示\ (T \通用电气48 \)的\ (\ texttt le 10 \ %{日军}\ \)推断,预测是可以接受的。延迟从21日之后\ \ (T = 62)稳定在11。

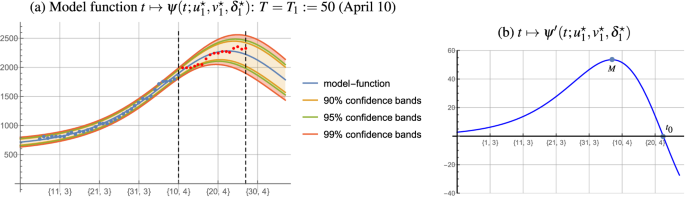
作为一个例子,同样是在“预测死亡的数量”,我们首先考虑训练数据的逐步增长的新病例\ (T = T_1: = 50 \)(4月10日),然后开始一段时间的训练数据,包括减少数量的新病例\ \ (T = T_2: = 70)(4月30日)。

物流模型的最优参数函数的累积数目的新病例\ (T = T_1: = 50 \)是\(^ \明星= 86231.7 \),\ (^ \ b星= 45.49 \),\ (c ^ \明星= 0.085 \)。解决共和党(9)\ (T = T_1: = 50 \)得到的最优参数\ (u ^ \明星_1 = 638.94 \),\ (v ^ \明星_1 = 0.900 \),\(δ^ \ \明星_1 = 17.35 \)模型的函数\ψ(\ \)由(8),因此平均延迟=δ}{\ \(\帽子_1 = 17 \)。图3显示了图模型的功能\ψ(\ \)(蓝色曲线)。红点代表住院天期间的实际数字4月10日。可视化也\ \ (90 \ %),\ \ (95 \ %),\ \ (99 \ %)信心乐队配合的功能\ψ(\ \),证明结果。这项措施\ (\ texttt{日军}= 3 \ % \)推断高度的协议我们的预测和住院天期间的实际数量从4月11日到4月28日,也就是显示在无花果。3导数的最大值\ψ(\ \)根据(12),达到4月7日,它的零点是4月22日(见图。3b)。这意味着,直到4月7日住院病人数量的增长是进步的,然后,直到4月22日,离题的,在4月22日住院的数量下降。

图3
图3

数量的住院,模型函数\ψ(\ \)有信心乐队的配合,导数\ψ(\ \)(\ (T_1: = 50 \))。

全尺寸图像

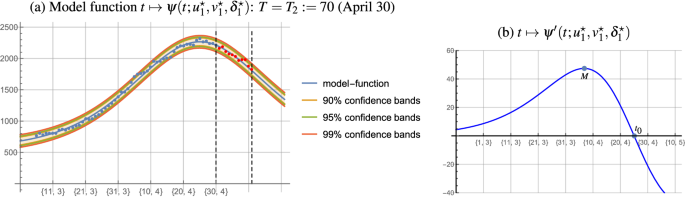
物流模型的最优参数函数的累积数目的新病例\ \ (T = T_2: = 70)(4月30日)\(^ \明星= 125072.0 \),\ (^ \ b星= 50.16 \),\ (c ^ \明星= 0.072 \)。解决共和党(9)\ \ (T = T_2: = 70)得到的最优参数\ (u ^ \明星_2 = 557.34 \),\ (v ^ \明星_2 = 0.758 \),\(δ^ \ \明星_2 = 10.71 \),平均延迟δ}{\ \(\帽子_2 = 11 \)。这项措施\ (\ texttt{日军}= 3.0 \ % \)推断高度的协议我们的预测和实际数字11天期间4月30日开始,也显示在无花果。4导数的最大值\ψ(\ \)达到4月7日,其空点是4月25日(见图。4b),也就是说,直到4月7日住院人数的增长是进步的,然后直到离题的4月25日,4月25日之后住院的数量下降。

图4
图4

数量的住院,模型函数\ψ(\ \)有信心乐队的配合,导数\ψ(\ \)(\ \ (T_2: = 70))。

全尺寸图像

结论

在我们的论文,我们提出一个现象学模型预测死亡和住院人数大流行波,假设线性依赖的,死亡的人数有一定延迟\ \(τ)> 0 \)新病例的数量,同样的,住院的数量线性依赖于新病例的数量与另一个延迟δ> 0 \ \ (\)。预测应每天使用日常数据在新情况下,死亡和住院的流行浪潮的开始。为此我们设计了专用的Mathematica笔记本电脑,免费http://models.mathos.unios.hr/。

使用该方法测试和演示数据的第三波COVID-19流行在克罗地亚,但该方法可以应用于任何COVID-19流行的新浪潮,以及任何其他可能的流感大流行。

同时,本文编写的第一个版本以来,无数的结果出现在各种作者处理同样的问题以不同的方式(见例如参考文献。1,11,18,19,20.)。我们的方法是简单的基本强度基于我们之前的工作21,22,23,29日,使用高效数值方法寻找最优模型的参数(见备注1),这也是基于我们之前的工作。除了死亡和住院每日数据,我们的模型使用的数据证实感染病例。但前提是一个好的方法检测或其他方式提出实际感染者的数量被发现,确诊病例的数据在我们的模型很容易被替换的数据实际上感染,使预测同样简单快速,但更加准确、可靠。我们的模型可以通过使用增强疫苗接种数据。

数据和计算机代码的可用性

评价都是使用我们自己的Mathematica模块死亡[]和住院[],免费的http://models.mathos.unios.hr/。这两个模块调用数据集Data.txt,也可以在这个url,包含新病例的数量、死亡和住院COVID-19的第三波大流行期间在克罗地亚。

该模块死亡[]输出为已故的累积数目的预测\({\τ}\ \帽子)天,死亡病例之间的比例\({\τ}\ \帽子)天前(参见“预测死亡的数量”)。结果给出了物流和龚帕兹模型函数。该模块还可以输出如下:

  • 新病例的条形图和死者的;

  • 最优参数相应的物流和龚帕兹模型函数的累积数目的新情况下,他们的图表,特征点和饱和水平,见参考文献。22,23;

  • 相关函数的最优参数\ \ varphi \ ()由(4),它的图形,信心乐队配合,特征点和死者的比例使用物流和龚帕兹模型函数;

该模块住院[]输出预期的数量在未来住院\(\帽子δ}{\ \)天(参见“预测住院的数量”)。结果给出了使用物流模型的功能。此外,该模块还可以输出如下:

  • 条形图的新病例的住院;

  • 物流模型的最优参数的函数累积数目的新病例,其图,和特征点,看到裁判。22;

  • 最优参数\ (u ^ \明星\),\ (v ^ \星\),\(δ^ \ \ * \)相关函数的\ψ(\ \)由(8),它的图形,信心乐队的配合,和特征点;

  • 的价值日军。