混合光子-声子封锁gydF4y2Ba

光子阻断(PB)gydF4y2Ba^1gydF4y2Ba，也称为光学状态截断(见参考文献综述。gydF4y2Ba^{2gydF4y2Ba，gydF4y2Ba3.gydF4y2Ba})，或非线性量子剪刀(有关评论请参阅参考文献。gydF4y2Ba^4gydF4y2Ba)是库仑封锁的光学模拟物。具体来说，它指的是在驱动非线性系统中产生的单个光子可以阻止更多光子的产生。由理想(或“真实”)PB产生的光既表现出亚泊松光子数统计又表现出光子反聚束。但是，即使满足了这些性质中的一个，也经常使用术语PB。gydF4y2Ba

在各种驱动非线性系统中，实验证明了该方法的有效性gydF4y2Ba^{5gydF4y2Ba，gydF4y2Ba6gydF4y2Ba，gydF4y2Ba7gydF4y2Ba，gydF4y2Ba8gydF4y2Ba，gydF4y2Ba9gydF4y2Ba，gydF4y2Ba10gydF4y2Ba，gydF4y2Ba11gydF4y2Ba}和两个gydF4y2Ba^{12gydF4y2Ba，gydF4y2Ba13gydF4y2Ba}谐振器，在一个双峰腔gydF4y2Ba^14gydF4y2Ba甚至在无腔系统中gydF4y2Ba^15gydF4y2Ba．观测PB的实验平台包括:带有Fabry-Perot腔的腔量子电动力学(QED)gydF4y2Ba^5gydF4y2Ba，光子晶体gydF4y2Ba^6gydF4y2Ba，以及低语廊模式空腔gydF4y2Ba^16gydF4y2Ba，以及电路QEDgydF4y2Ba^{7gydF4y2Ba，gydF4y2Ba8gydF4y2Ba}．请注意，在非线性克尔介质驱动腔中产生单光子态的可能性已经在Refs中得到了预测。gydF4y2Ba^{17gydF4y2Ba，gydF4y2Ba18gydF4y2Ba，gydF4y2Ba19gydF4y2Ba}，但仅限于Ref的出版。gydF4y2Ba^1gydF4y2Ba在美国，“光子封锁”这一术语被创造出来，引发了人们对理论和实验研究这一效应的浓厚兴趣。可以说，在20世纪70年代和80年代已经有许多关于光子反聚束和亚泊松光的研究报告(参见参考文献中的评论)。gydF4y2Ba^{20.gydF4y2Ba，gydF4y2Ba21gydF4y2Ba，gydF4y2Ba22gydF4y2Ba}和其中的参考文献)实际上是关于pb相关的效应，尽管这种关系(与库仑封锁的光学类似物)在那里没有明确提到。gydF4y2Ba

除了原先设想的利用PB作为单光子旋转门装置外，还采用了单光子旋转门gydF4y2Ba^{1gydF4y2Ba，gydF4y2Ba16gydF4y2Ba，gydF4y2Ba23gydF4y2Ba}或多个gydF4y2Ba^24gydF4y2Ba结果表明，PB在单光子水平的量子非线性光学中有更广泛的应用，包括单光子诱导的非线性效应，通过光子反聚束来降低量子噪声，非互易非线性过程的模拟，或在量子计量学中研究异常点的手性等。gydF4y2Ba

许多标准单光子效应被提出，其中包括:(1)双光子和多光子的PB版本，正如在Refs中首次预测的那样。gydF4y2Ba^{25gydF4y2Ba，gydF4y2Ba26gydF4y2Ba}并在Refs中进行了实验证明。gydF4y2Ba^{11gydF4y2Ba，gydF4y2Ba27gydF4y2Ba}；(2)如Ref.预测的非常规PB。gydF4y2Ba^28gydF4y2Ba并在参考文献中实验证明。gydF4y2Ba^{12gydF4y2Ba，gydF4y2Ba13gydF4y2Ba}；(3)文献预测的常规和非常规PB非互反效应。gydF4y2Ba^{29gydF4y2Ba，gydF4y2Ba30.gydF4y2Ba}并且(至少部分地)在参考文献中被实验证实。gydF4y2Ba^31gydF4y2Ba；(4)状态依赖PBgydF4y2Ba^32gydF4y2Ba(5)例外PBgydF4y2Ba^33gydF4y2Ba(6)基于条件测量的线性量子剪刀:单pbgydF4y2Ba^{34gydF4y2Ba，gydF4y2Ba35gydF4y2Ba，gydF4y2Ba36gydF4y2Ba}，这在文献中得到了实验证明。gydF4y2Ba^37gydF4y2Ba，以及two-PBgydF4y2Ba^38gydF4y2Ba、多pbgydF4y2Ba^{39gydF4y2Ba，gydF4y2Ba40gydF4y2Ba}使用多端口马赫-曾德干涉仪gydF4y2Ba^41gydF4y2Ba．这种概率的PB方法也可以实现非确定性量子隐形传态和更有选择性的光学状态截断，例如，希尔伯特空间中的洞燃烧gydF4y2Ba^42gydF4y2Ba．对于例(2)，请注意双驱动克尔谐振腔中的PB是在Refs中首次研究的。gydF4y2Ba^{43gydF4y2Ba，gydF4y2Ba44gydF4y2Ba}，但仅适用于相对强的克尔非线性。令人惊讶的是，PB仍然在这样的双谐振腔系统中，即使是非常弱的克尔非线性，正如Ref中首次预测的那样。gydF4y2Ba^28gydF4y2Ba并在参考文献中通过破坏性量子干涉解释。gydF4y2Ba^45gydF4y2Ba．这种效应现在被称为非常规PBgydF4y2Ba^46gydF4y2Ba．gydF4y2Ba

这里我们研究声子封锁gydF4y2Ba^47gydF4y2Ba，这是上述阻塞效应的力学模拟，即机械谐振腔的量子振动激励的阻塞。这种效应尚未在实验中得到证实。然而，已经提出了一些实验上可行的方法来测量它，包括磁动机技术gydF4y2Ba^47gydF4y2Ba，一种通过光学干涉法间接测量声子相关性的方法gydF4y2Ba^48gydF4y2Ba，或通过将机械谐振器耦合到量子位，这不仅用于诱导谐振器非线性，而且还用于检测封锁效应本身，即通过测量量子位的状态gydF4y2Ba^49gydF4y2Ba．在声子封锁的可能应用中，我们提到:测试介观或宏观力学系统的非经典性gydF4y2Ba^47gydF4y2Ba研究单声子光力学，提供单声子或多声子的源gydF4y2Ba^{50gydF4y2Ba，gydF4y2Ba51gydF4y2Ba}．gydF4y2Ba

PB可以改成透光gydF4y2Ba^52gydF4y2Ba例如，通过光子诱导隧穿(PIT)gydF4y2Ba^6gydF4y2Ba．这是另一种非经典光子数相关现象，在系统的较高流形中观察到更多光子的概率随着系统共振频率附近的第一个光子的产生而增加。同时还预测了多重pit效应gydF4y2Ba^29gydF4y2Ba，包括挤压产生的gydF4y2Ba^53gydF4y2Ba．gydF4y2Ba

为了简单起见，我们在这里使用缩写PB，不仅指光子的封锁，而且指声子或混合光子-声子玻色子的封锁。确切的含义可以从上下文中找到，例如，当我们提到一个特定的模式时，包括光学(gydF4y2Ba一个gydF4y2Ba)、机械(gydF4y2BabgydF4y2Ba)，或混合(gydF4y2BacgydF4y2Ba)模式。类似地，PIT表示在三种类型的激发中给定的粒子诱导隧穿。gydF4y2Ba

纳米机械谐振腔能与电磁辐射发生相干相互作用gydF4y2Ba^54gydF4y2Ba，研究了单纠缠光子-声子对中单光子与单声子之间的量子相关性gydF4y2Ba^55gydF4y2Ba或者通过光机械系统中的光子和声子阻塞效应gydF4y2Ba^56gydF4y2Ba．最近研究了一种PB和PIT之间的机械切换gydF4y2Ba^57gydF4y2Ba．由机械谐振器和光学谐振器组成的系统中的PB和PIT效应，其特征是相同或相似的裸频率，据我们所知，尚未在实验上进行研究，尽管它们在实验上似乎是可行的，因此它们是本文的重点。gydF4y2Ba

PB和PIT的关键特征可以通过测量二阶相关函数来观察，gydF4y2Ba\ (g ^ {(2)} (0) \)gydF4y2Ba．对于光子，(1)的条件gydF4y2Ba\ (g ^ {(2)} (0) < 1 \)gydF4y2Ba定义了亚泊松光子数统计量(也称为零延迟光子反聚束)，它表明了观测PB的可能性，而(2)条件gydF4y2Ba\ (g ^ {(2)} (0) > 1 \)gydF4y2Ba，定义了超泊松统计量(也称为零延迟光子聚束)，这是给定系统中PIT的一个特征。要观察PB和PIT的“真实”效应，还需要满足其他标准，如非零延迟光子反聚束和高阶亚泊松光子数统计。事实上，一个理想的常规PB，可以作为单光子源，通常也应该通过研究高阶相关函数来验证，gydF4y2Ba\ (g ^ {(n)} (0) \)gydF4y2Ba为gydF4y2Ba\ (n > 2 \)gydF4y2Ba．例如单pb (1PB)情况gydF4y2Ba\ (g ^ {(2)} (0) < 1 \)gydF4y2Ba而且gydF4y2Ba\ (g ^ {(n)} (0) < 1 \)gydF4y2Ba为gydF4y2Ba\ (n > 2 \)gydF4y2Ba应该得到满足。gydF4y2Ba

PB也可以通过演示的其他方式来验证，例如，平均光子数(或通过非线性谐振器传输的测量功率)对入射到谐振器上的光子的能谱的楼梯状依赖gydF4y2Ba^{8gydF4y2Ba，gydF4y2Ba52gydF4y2Ba}．这种依赖关系是光子的库仑阶梯。以上所有标准都是证明PB的必要条件，而不是充分条件。一个充分条件可以是，例如，显示一个给定的生成光(具有非零的平均光子数)的高保真度到一个理想的截断二维状态，这是最接近生成的状态。这种方法被应用于，例如，gydF4y2Ba^{26gydF4y2Ba，gydF4y2Ba35gydF4y2Ba，gydF4y2Ba36gydF4y2Ba}．但本文并未采用后两种类型的PB测试。gydF4y2Ba

由于给定系统的非线性，传统的单pb阻止了对特定频率的第二光子的吸收。这种非线性可以用克尔型相互作用来描述，并且/或可以由耦合到谐振腔的原子(真原子或人造原子)诱导。人造原子可以通过量子点来实现gydF4y2Ba^{23gydF4y2Ba，gydF4y2Ba58gydF4y2Ba，gydF4y2Ba59gydF4y2Ba}腔内QEDgydF4y2Ba^10gydF4y2Ba或电路QED中的超导量子比特或量子比特gydF4y2Ba^52gydF4y2Ba．gydF4y2Ba

由破坏性干涉诱导的非常规PB，在极低(甚至极低)平均光子数下工作得更好gydF4y2Ba^{12gydF4y2Ba，gydF4y2Ba13gydF4y2Ba}．这可能是不利的，因为它大大降低了产生单个光子的概率。但是，与此同时，这可能是一个优势，因为非常小的平均光子数通常会降低产生多光子态和诱导高阶相干的机会。但情况并非总是如此，即使观测到两个光子的概率被抑制，高阶相干性也可能被增强，从而导致多光子态的产生gydF4y2Ba^46gydF4y2Ba．gydF4y2Ba

在本文中，我们考虑一个光机械系统，它产生光子和声子模式。然后我们对这些模式应用平衡线性耦合变换来创建混合模式(也称为超模式)。我们研究了光子和声子之间的相互作用，从而导致它们的非经典数相关效应。因此，我们找到了在四种模式下观测PB或PIT的系统参数。特别地，我们预测了混合模式之一的PB，而不是单个模式(光子和声子)的PB，也就是说，这个PB是由两种模式创建的，它们不表现出PB。我们将这种效应称为混合光子-声子封锁，这是本文报道的主要结果。gydF4y2Ba

具体来说，我们将混合光子-声子封锁定义为通过平衡线性耦合器将光学或微波模式的光子与机械模式的声子耦合而获得的混合模式玻色子(极化子)的封锁。测试这种类型的封锁的想法和标准类似于其他已知的封锁效应(例如光子、声子或磁振子)，但它是对另一种类型的玻色子的预测。我们证明了这种混合封锁可以通过耦合模式发生，既不表现出光子封锁也不表现出声子封锁。gydF4y2Ba

为了显示这种效应，我们分析了两个线性耦合谐振器的系统:一个超导微波谐振器(SMR)，它可能是一个传输线谐振器，和一个微机械谐振器，称为量子鼓(QD)，它是电容耦合到SMR。要生成任何类型的PB(包括非常规PB)，需要将非线性纳入给定的系统gydF4y2Ba^{17gydF4y2Ba，gydF4y2Ba60gydF4y2Ba，gydF4y2Ba61gydF4y2Ba}．这可以通过将一个谐振器(如SMR)耦合到一个量子比特(如人工超导两能级原子)来实现。我们还假设系统由QD或SMR驱动，这将在下一节中详细描述。gydF4y2Ba

本文的组织结构如下:首先，介绍了混合光机系统及其哈密顿量。我们还定义了混合光子-声子模式，它可以由光子和声子模式的平衡线性耦合产生。然后，我们分别研究了在光学或机械谐振腔驱动的系统中的光子，声子和其中一个混合模式中的相关效应，以实验上可行的参数指定在“gydF4y2Ba方法gydF4y2Ba”。然后，我们通过非厄米哈密顿方法预测并分析解释了非传统混合模式封锁的产生。我们系统地研究了在我们的系统中观察阻塞和隧道效应的不同弱和强标准。在这3种模式下，我们还发现了常规封锁和隧道效应的全部8种组合。特别是，我们发现了一个令人惊讶的效应，即混合模式的光子-声子封锁可以通过混合光子和声子模式产生隧道效应。本文除了研究二阶相关效应外，还讨论了高阶相关效应及其分类。gydF4y2Ba方法gydF4y2Ba”。此外，我们讨论了两种测量混合模式下光子-声子相关性的方案。最后，我们总结了我们的研究成果并指出了它们的潜在应用。gydF4y2Ba

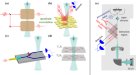
数字gydF4y2Ba1gydF4y2Ba显示了所研究的混合系统的原理图，该混合系统由一个超导两能级人工原子(一个量子比特)嵌入波导并耦合到一个SMR，这可能是一个传输线谐振器。这个量子比特在SMR中诱导了非谐性，这对于观察PB是至关重要的。我们的设置还包括一个微波频率机械谐振器(QD)，它是电容耦合到SMR。量子点的非线性是由量子点与有效非线性SMR的线性耦合间接引起的。gydF4y2Ba

SMR的自由汉密尔顿量是gydF4y2Ba\(H_a=\hbar \omega _{_\math {SMR}} a^\dagger a\)gydF4y2Ba,在那里gydF4y2Ba\ \(ω_ {_ \ mathrm鼻中隔黏膜下切除术后{}}\)gydF4y2Ba它的共振频率(这里假设是几十GHz)和gydF4y2Ba\ \(,(^{\匕首})\)gydF4y2Ba是光子湮灭(产生)算符。我们可以合理地假设SMR质量因子为gydF4y2Ba鼻中隔黏膜下切除术后\ (Q_ {_ \ mathrm{}} \大约10 ^ 4 \)gydF4y2Ba．QD的自由哈密顿量是gydF4y2Ba\(H_b=\hbar \ ω _m b^\dagger b\)gydF4y2Ba,在那里gydF4y2Ba\ω_m (\ \)gydF4y2Ba它的共振频率和gydF4y2Ba\ \ (b, b(^{\匕首}),\ \)gydF4y2Ba是声子湮灭(产生)算符。在数值模拟中，我们设gydF4y2Ba\(\omega _m/2\pi =7.8\)gydF4y2BaGHz和QD质量因子为gydF4y2Ba\ (Q_m \ \)约260gydF4y2Ba．此外，两能级量子系统具有基态gydF4y2Ba\(| g \rangle\)gydF4y2Ba激发态gydF4y2Ba\(| e\ rangle\)gydF4y2Ba有转换频率gydF4y2Ba\ω_q (\ \)gydF4y2Ba(此处按顺序排列gydF4y2Ba\ω_m (\ \)gydF4y2Ba而且gydF4y2Ba\ \(ω_ {_ \ mathrm鼻中隔黏膜下切除术后{}}\)gydF4y2Ba)．自由量子比特的哈密顿量被描述为gydF4y2Ba\ (H_q = \百巴\ω_ {q} \σσ_ {-}_ {+}\ \)gydF4y2Ba,在那里gydF4y2Ba\(\sigma _{+}=| e \rangle \langle g |\)gydF4y2Ba（gydF4y2Ba\(\sigma _{-}=| g \rangle \langle e |\)gydF4y2Ba)是原子上升(下降)操作符。因此，系统的总自由哈密顿量为gydF4y2Ba\ (H_0 = H_a + H_b + H_q \)gydF4y2Ba．耦合系统的完全哈密顿量(无驱动)可由(gydF4y2Ba\(\ \百巴= 1)gydF4y2Ba）gydF4y2Ba

其中包括三个耦合项:(1)在旋转波近似(RWA)下描述SMR与量子比特相互作用的jayne - cummings项;(2)具有耦合强度的辐射-压力项gydF4y2Ba\ (g_r \)gydF4y2Ba；(3)具有强度的hopfield型非线性耦合项gydF4y2Ba\ (g_l \)gydF4y2Ba．的gydF4y2Ba\ (g_l \)gydF4y2Ba可通过电容实现耦合，如图所示。gydF4y2Ba1gydF4y2Ba并在参考文献中有更详细的解释。gydF4y2Ba^48gydF4y2Ba对于类似的系统。注意gydF4y2Ba\ (g_l \)gydF4y2Ba术语描述了规范的位置-位置(动量-位置)相互作用，其中gydF4y2Ba\ (g_l \)gydF4y2Ba实(虚)为何物gydF4y2Ba\ (H ' _ {+} \)gydF4y2Ba（gydF4y2Ba\ (H ' _ {-} \)gydF4y2Ba)．这些交互作用可以通过添加gydF4y2Ba\ \(π/ 2 \)gydF4y2Ba阶段gydF4y2Ba\({, ^ \匕首}\)gydF4y2Ba,也就是说,gydF4y2Ba\(a\右tarrow I a\)gydF4y2Ba而且gydF4y2Ba\(a^\dagger \rightarrow -i a^\dagger\)gydF4y2Ba．这个额外的相位不会改变模态中的数字相关性gydF4y2Ba一个gydF4y2Ba而且gydF4y2BabgydF4y2Ba．在模拟超导电路的典型参数范围内gydF4y2Ba^62gydF4y2Ba,gydF4y2Ba\ (g_l \)gydF4y2Ba项占主导地位，因此辐射-压项可以忽略gydF4y2Ba^63gydF4y2Ba．此外，虽然反向旋转的术语gydF4y2Ba\(ab\pm b^\dagger a^\dagger\)gydF4y2Ba，出现在gydF4y2Ba\ (g_l \)gydF4y2Ba-相互作用，在超强耦合和深强耦合体系中发挥重要作用gydF4y2Ba^64gydF4y2Ba，但在RWA下可以安全地省略它们，这在弱耦合和强耦合情况下都是有效的。事实上，本文只研究后一种制度，如下文所述。然后是Hopfield非线性gydF4y2Ba\ (g_l \)gydF4y2Ba-相互作用变得有效线性化。因此，哈密顿量(gydF4y2Ba1gydF4y2Ba)折算为gydF4y2Ba

其中线性耦合强度表示为gydF4y2BafgydF4y2Ba，替换符号gydF4y2Ba\ (g_l \)gydF4y2Ba．类似地,gydF4y2Ba\ (g_l \)gydF4y2Ba，gydF4y2BafgydF4y2Ba实(虚)为何物gydF4y2Ba\ (H_ {+} \)gydF4y2Ba（gydF4y2Ba\ (H_ {-} \)gydF4y2Ba)．在下面，为了简单起见，我们将重点研究模之间的规范位置-位置相互作用gydF4y2Ba一个gydF4y2Ba而且gydF4y2BabgydF4y2Ba，描述为gydF4y2Ba\ (H_ {+} \)gydF4y2Ba．哈密顿量的特征态gydF4y2Ba下午\ (H_ {\} \)gydF4y2Ba可以被称为原子光机械极化激元或原子腔力学极化激元gydF4y2Ba^65gydF4y2Ba．很明显，汉密尔顿函数gydF4y2Ba下午\ (H_ {\} \)gydF4y2Ba保留偏振子数，gydF4y2Ba

也就是激发的总数。因此,gydF4y2Ba下午\ (H_ {\} \)gydF4y2Ba可以在每个子空间(或流形)中对角化gydF4y2Ba\ (\ mathcal {H} ^ {(n)} \)gydF4y2Ba与完全gydF4y2BangydF4y2Ba极化声子。gydF4y2Ba

RWA是完全合理的，假设(1)弱耦合或强耦合和(2)SMR和QD之间的小失谐，以及SMR和量子位之间的小失谐(参见，例如，Ref。gydF4y2Ba^66gydF4y2Ba)．我们强调，本文所采用的数值计算参数完全满足这些条件。因此，可以应用杰恩斯-卡明斯模型和频率转换器(或线性耦合器)模型。然而，RWA不能应用于定义的超强和深强耦合体系gydF4y2Ba\(g> 0.1\，\omega _{i}\)gydF4y2Ba而且gydF4y2Ba\ (g > \ω_{我}\)gydF4y2Ba分别gydF4y2Ba^64gydF4y2Ba,在那里gydF4y2Ba\(i=\ mathm {SMR}， m, q\)gydF4y2Ba．在这种情况下，量子Rabi模型和Hopfield模型不能分别简化为jayes - cummings模型和变频器模型。但是，我们研究的是公式中指定的参数。（gydF4y2Ba28gydF4y2Ba) - (gydF4y2Ba30.gydF4y2Ba)，其中耦合强度与频率之比，gydF4y2Ba\ (f /ω_i \ \)gydF4y2Ba而且gydF4y2Ba\ (g / \ω_i \)gydF4y2Ba,都是gydF4y2Ba\ (< 0.002 \)gydF4y2Ba．因此，该系统处于强耦合状态，远离USC状态的边界。此外，所选失谐为gydF4y2Ba\(| \ω_ {_ \ mathrm鼻中隔黏膜下切除术后{}}- \ω_m | /ω\ _ {_ \ mathrm鼻中隔黏膜下切除术后{}}\ le 2.6 \ * 10 ^ {3} \)gydF4y2Ba而且gydF4y2Ba\(| \ω_ {_ \ mathrm鼻中隔黏膜下切除术后{}}- \ω_q | /ω\ _ {_ \ mathrm鼻中隔黏膜下切除术后{}}< 8 \ * 10 ^ {4}\)gydF4y2Ba．因此，可以清楚地看到，我们可以安全地应用RWA。无论如何，作为双重检验，我们已经计算了哈密顿量的随时间变化的二阶相关函数gydF4y2Ba\ (H ' _{下午\}\)gydF4y2Ba而且gydF4y2Ba下午\ (H_ {\} \)gydF4y2Ba参阅式中所设参数。（gydF4y2Ba28gydF4y2Ba) - (gydF4y2Ba30.gydF4y2Ba)，假设经典驱动(如下所述)并且没有耗散。我们发现，在有RWA和没有RWA的模型中计算的相关函数之间的差异在数字尺度上可以忽略不计。在系统中包含耗散使这种差异更小。gydF4y2Ba

我们假设光泵浦场的频率gydF4y2Ba\(ω_ {p} \ \)gydF4y2Ba是否应用于SMR模式gydF4y2Ba一个gydF4y2Ba，描述为gydF4y2Ba

或到QD模式gydF4y2BabgydF4y2Ba，由gydF4y2Ba

(用耦合强度)驱动(激发)系统gydF4y2Ba\(η_{一}\ \)gydF4y2Ba或gydF4y2Ba\(η_ {b} \ \)gydF4y2Ba)并诱导光子和声子的发射。这样，总哈密顿量就变成了gydF4y2Ba

QD的直接驱动可以通过弱振荡电流实现，如参考文献中所考虑的那样。gydF4y2Ba^{47gydF4y2Ba，gydF4y2Ba48gydF4y2Ba}，哪里驱力大gydF4y2Ba\(η_b \ \)gydF4y2Ba与电流幅值成正比gydF4y2Ba我gydF4y2Ba（gydF4y2BatgydF4y2Ba)和磁场gydF4y2BaBgydF4y2Ba如图所示。gydF4y2Ba1gydF4y2Ba．SMR可以在电路qed系统中以各种方式驱动gydF4y2Ba^62gydF4y2Ba．gydF4y2Ba

请注意，通过直接驱动SMR(或QD)，也可以通过电容耦合间接驱动QD (SMR)gydF4y2Ba\ (C_g \)gydF4y2Ba，如图方案所示。gydF4y2Ba1gydF4y2Ba．因此，通过提到SMR或qd驱动系统，我们只指出谐振器，它是直接泵浦的，尽管最终两个谐振器都是驱动的。gydF4y2Ba

在量子d中包含额外的非线性和/或将驱动器应用于量子比特和两个谐振器对于混合封锁的预测不是必要的，但这可以实现更强的光子-声子反聚束和更多的亚泊松统计。gydF4y2Ba

考虑泵场仅驱动SMR的情况，以消除哈密顿量的时间依赖性gydF4y2Ba\ (H ^ {(n)} (t) \)gydF4y2Ba为了得到它的稳态解，我们将系统的哈密顿量转换成一个以频率旋转的参考系gydF4y2Ba\ω_p (\ \)gydF4y2Ba．gydF4y2Ba

我们应用幺正变换gydF4y2Ba= \ exp \ \ (U_R (t)左(我N_ \ mathrm{极化声子}\ω_p t \) \)gydF4y2Ba来gydF4y2Ba\ (H ^ {(n)} \)gydF4y2Ba根据一般公式gydF4y2Ba

因此,gydF4y2Ba\ (H ^ {(a)} (t) \)gydF4y2Ba减少时间无关的smr驱动哈密顿量:gydF4y2Ba

在哪里gydF4y2Ba\(\Delta _{i}=\omega _{i}-\omega _{p}\)gydF4y2Ba为gydF4y2Ba\ (i = a、b问\)gydF4y2Ba．所以，特别地，gydF4y2Ba\(\Delta _{b}\equiv \Delta _{m}\)gydF4y2Ba（gydF4y2Ba\(\Delta _{a}\相等\Delta _{_\数学{SMR}}\)gydF4y2Ba)是机械(微波)谐振腔频率相对于泵浦频率的失谐。类似地，在同一个旋转的坐标系中，gydF4y2Ba\ (H ^ {(b)} (t) \)gydF4y2Ba简化为qd驱动的哈密顿量:gydF4y2Ba

我们回忆一下等式。（gydF4y2Ba8gydF4y2Ba)及(gydF4y2Ba9gydF4y2Ba)直接由式(gydF4y2Ba6gydF4y2Ba)gydF4y2Ba\ (H_ + \)gydF4y2Ba如式所示(gydF4y2Ba2gydF4y2Ba)．此外,gydF4y2Ba\ (H_ + \)gydF4y2Ba由式(gydF4y2Ba1gydF4y2Ba)假设RWA，这对于弱耦合和强耦合体系中的小失谐是合理的，这是本文中唯一的数值研究体系，如上所强调的。的确，所研究的参数范围保证了系统的演化远离USC体系。注意哈密顿量gydF4y2Ba\ (H ' _ + \)gydF4y2Ba在(gydF4y2Ba1gydF4y2Ba)gydF4y2Ba\ (g_r = 0 \)gydF4y2Ba加上一个附加的驱动项gydF4y2Ba\ (H ^ {(n)} _ \ mathrm {drv} (t) \)gydF4y2Ba，根据式(gydF4y2Ba7gydF4y2Ba),gydF4y2Ba\ (H ^ {(n)} _ \ mathrm{腐烂}\)gydF4y2Ba如式所示。（gydF4y2Ba8gydF4y2Ba)及(gydF4y2Ba9gydF4y2Ba)，但附加了一个术语gydF4y2Ba\(f[a b \exp (2i\omega _p t)+\math {h.c.}]\)gydF4y2Ba．在所有的数值计算中gydF4y2Ba\ω_p (\ \)gydF4y2BaGHz级。因此，这个快速振荡项的影响与哈密顿量中的所有其他项相比可以忽略不计。此外，我们还假设了光力学术语gydF4y2Ba\ (g_r \)gydF4y2Ba是微不足道的。一般来说，这个假设是不必要的，因为gydF4y2Ba\ (g_r \)gydF4y2Ba项可以简化为描述线性耦合器(或分束器)的相互作用项(在红失谐状态下)，它可以与gydF4y2BafgydF4y2Ba术语。总之，为了简化理论和潜在实验，我们设gydF4y2Ba\ (g_r = 0 \)gydF4y2Ba．我们还假设系统以机械模式或光学模式驱动，以获得有效的时间无关的哈密顿量。如果考虑系统同时以不同频率的两种模式驱动，这种简化是不可能实现的。gydF4y2Ba

数字gydF4y2Ba2gydF4y2Ba为混合系统哈密顿量的能谱结构(gydF4y2Ba2gydF4y2Ba)．为了研究混合模式下的亚泊松光产生，我们对SMR和QD模式应用了平衡线性耦合变换，它在形式上等价于平衡(50/50)分束器(BS)。这种转换产生了混合(或交叉)光子-声子模式:gydF4y2Ba

对于所描述的系统gydF4y2Ba\ (H_ + \)gydF4y2Ba以及相关的汉密尔顿公式。注意，如果这个BS转换被修改为gydF4y2Ba\(a\rightarrow -i a\)gydF4y2Ba而且gydF4y2Ba\(a^\dagger \rightarrow I a^\dagger\)gydF4y2Ba弥补了额外的损失gydF4y2Ba\ \(π/ 2 \)gydF4y2Ba式(gydF4y2Ba1gydF4y2Ba)]，然后我们对混合模式中各种数字相关性的预测gydF4y2BacgydF4y2Ba(除了那些模式gydF4y2Ba一个gydF4y2Ba，gydF4y2BabgydF4y2Ba,gydF4y2BadgydF4y2Ba)与所描述的模型相同gydF4y2Ba\ (H_ (\)gydF4y2Ba．gydF4y2Ba

因此，哈密顿量gydF4y2Ba\ (H \)gydF4y2Ba在BS转换读取之后gydF4y2Ba

这描述了量子比特与两种混合模式的相互作用gydF4y2BacgydF4y2Ba而且gydF4y2BadgydF4y2Ba,在那里gydF4y2Ba\ \(δ_ {c, d} =ω(\ _ {_ \ mathrm鼻中隔黏膜下切除术后{}}+ \ω_m) / 2 - f下午\ω_p \ \)gydF4y2Ba而且gydF4y2Ba\ \(δ=ω(\ _ {_ \ mathrm鼻中隔黏膜下切除术后{}}- \ω_m) / 2 \)gydF4y2Ba．可以看出，这两种模态gydF4y2BacgydF4y2Ba而且gydF4y2BadgydF4y2Ba如果没有直接耦合gydF4y2Ba\(\ ω _m=\ ω _{_\数学{SMR}}\)gydF4y2Ba．gydF4y2Ba

在马尔科夫近似下存在损耗的开放系统的动力学可以在林德布莱德方法中描述系统的约简密度矩阵gydF4y2Baρ\ (\ \)gydF4y2Ba满足标准主方程，gydF4y2Ba

它是用林德布莱德超算符给出的gydF4y2Ba\ (\ mathscr {D} [O] \ρ= \压裂{1}{2}(2 O \ρO ^ \匕首- O - O ^ \ \ρO ^ \匕首短剑O \ρ)\)gydF4y2Ba,在那里gydF4y2Ba\ (\ kappa _a \)gydF4y2Ba，gydF4y2Ba\ (\ kappa _b \)gydF4y2Ba而且gydF4y2Ba\γ(\ \)gydF4y2Ba分别为SMR、QD和量子比特的衰减率。gydF4y2Ba

我们给出了系统参数的数值计算和分析，这些参数满足SMR、QD和量子位之间的弱耦合和强耦合以及小失谐的条件。因此，我们可以安全地应用Eq.(中给出的标准主方程。gydF4y2Ba12gydF4y2Ba)．当然，如果考虑Eq. (gydF4y2Ba1gydF4y2Ba)，则Eq. (gydF4y2Ba12gydF4y2Ba)，应由一个广义的，如Refs。gydF4y2Ba^{64gydF4y2Ba，gydF4y2Ba67gydF4y2Ba，gydF4y2Ba68gydF4y2Ba，gydF4y2Ba69gydF4y2Ba}．gydF4y2Ba

我们还注意到，在强耦合条件下，即使将单个经典驱动器应用于Jaynes-Cummings模型，也会有效地产生反向旋转项，这可以诱导各种USC效应，如Ref中明确显示的那样。gydF4y2Ba^70gydF4y2Ba．因此，为了确认我们结果的有效性，我们应用了参考文献中描述的广义形式主义。gydF4y2Ba^67gydF4y2Ba，该方法适用于任意光物质耦合态，包括弱态、强态和USC态。特别地，我们计算了相关函数gydF4y2Ba\ (g ^ {(n)} (0) \)gydF4y2Ba根据正- (gydF4y2Ba\ (X ^ + _n”\)gydF4y2Ba)和负- [gydF4y2Ba\ (X ^ _n”= (X ^ + _n”)^{\匕首}\)gydF4y2Ba正则位置算子的频率分量:gydF4y2Ba\(X_a = a + a^{\dagger}\)gydF4y2Ba为光子,gydF4y2Ba\ (X_b = b + b ^{\匕首}\)gydF4y2Ba对于声子，和gydF4y2Ba\ (X_c = c + c ^{\匕首}\)gydF4y2Ba量子比特- smr - qd修饰基中的混合模玻色子。通过数值求解Ref的广义主方程，计算了系统的稳态。gydF4y2Ba^67gydF4y2Ba哈密顿公式gydF4y2Ba\ (H \)gydF4y2Ba而且gydF4y2Ba\ (H”\)gydF4y2Ba．根据一般的考虑，我们对公式中所设参数的数值计算。（gydF4y2Ba28gydF4y2Ba) - (gydF4y2Ba30.gydF4y2Ba)，使用标准和一般化的形式gydF4y2Ba\ (H \)gydF4y2Ba(以及gydF4y2Ba\ (H”\)gydF4y2Ba)会得到相同的结果。gydF4y2Ba

在我们的模拟中，我们假设系统是在基态下准备的gydF4y2Ba\(| n=0, g \rangle | m=0 \rangle\)gydF4y2Ba(即SMR中没有光子，QD中没有声子，量子比特处于基态)，这样给定的泵浦激光器可以在微波频率范围内驱动SMR光子。请注意，初始状态的选择影响我们系统的短时演化，但对时间限制内的稳态解没有影响，假设单光子和单声子阻尼通道，如式(gydF4y2Ba12gydF4y2Ba)．然而，如参考文献所示。gydF4y2Ba^32gydF4y2Ba，在量子工程耗散通道只允许双光子耗散的情况下，系统的初始状态确实会影响系统的稳态，因此也会改变PB。gydF4y2Ba

在接下来的章节中，我们展示了与SMR、QD和量子位的衰减率相比，在弱、中等和强耦合状态下，可以在混合模式下观察PB和PIT。特别地，我们证明了该系统可以通过混合具有强超泊松(或亚泊松)统计量的SMR和QD模式来生成具有强亚泊松(或亚泊松)统计量的混合光子-声子模式。gydF4y2Ba

本文详细分析了由哈密顿量描述的smr驱动耗散系统中的各种阻塞和PIT效应gydF4y2Ba\ (H \)gydF4y2Ba主方程(gydF4y2Ba12gydF4y2Ba)，以获取式(gydF4y2Ba28gydF4y2Ba)．gydF4y2Ba

我们的混合系统所产生的模式的光子/声子数统计量可以通过计算零延迟时间来定量描述gydF4y2Ba\ (k \ hbox {th} \)gydF4y2Ba-阶相关函数(gydF4y2Ba\ (k \ hbox {th} \)gydF4y2Ba-阶强度自相关函数)，gydF4y2Ba

在哪里gydF4y2Ba\ (z = a, b, c, d \)gydF4y2Ba而且gydF4y2Ba\ (k = 2 3 \ ldots \)gydF4y2Ba．在特殊情况下gydF4y2Ba\ (k = 2 \)gydF4y2Ba，这是特别感兴趣的测试单pb和单pit，三种不同类型的玻色子数统计可以考虑:泊松[如果gydF4y2Ba\ (g ^ {(2)} (0) = 1 \)gydF4y2Ba， super-Poissonian[如果gydF4y2Ba\ (g ^ {(2)} (0) > 1 \)gydF4y2Ba]和亚泊松(否则)。类似地，我们可以定义的高阶Poissonian，亚Poissonian和超Poissonian统计量gydF4y2Ba\ (k > 2 \)gydF4y2Ba．这种高阶准则不仅对分析多pb和多pit效应至关重要gydF4y2Ba^{11gydF4y2Ba，gydF4y2Ba29gydF4y2Ba，gydF4y2Ba53gydF4y2Ba}但它们在测试特定的PB效应是否是“真正的”PB(可用于产生单光子或声子)时也很重要。这些高阶统计量在“gydF4y2Ba方法gydF4y2Ba”。gydF4y2Ba

数字gydF4y2Ba3.gydF4y2Ba(一个)显示gydF4y2Ba\ (g ^ {(2)} (0) \)gydF4y2Ba作为smr驱动系统的量子位- smr耦合的函数，其参数在Eq. (gydF4y2Ba28gydF4y2Ba)．区域，当亚泊松统计在混合模式gydF4y2BacgydF4y2Ba模态中的超泊松统计量gydF4y2Ba一个gydF4y2Ba而且gydF4y2BabgydF4y2Ba，在本图和其他图中以黄色背景表示。表中黄色区域称为案例7gydF4y2Ba1gydF4y2Ba，其中我们在SMR (QD)中观察到强烈的超泊松光子(声子);而在混合模式下观察到的是单一激励。导致情形7的系统参数由数值模拟得到，并在下面讨论。gydF4y2Ba

注意图。gydF4y2Ba3.gydF4y2BaA显示了强耦合状态下的这些效应gydF4y2Ba^64gydF4y2Ba，即量子位- smr耦合常数gydF4y2BaggydF4y2Ba大于系统阻尼率:gydF4y2Ba\(g/\kappa _\ mathm {\max}>1\)gydF4y2Ba,在那里gydF4y2Ba\ (\ kappa _ \ mathrm{\马克斯}= \马克斯\ {\ kappa _a \ kappa _b \伽马\}\)gydF4y2Ba．另一方面，无花果。gydF4y2Ba3.gydF4y2BaB在弱耦合状态下也有相同的黄色区域，即gydF4y2Ba\(g/\kappa _\mathrm{\max}<1\)gydF4y2Ba，但是这个数字是为qd驱动系统计算的，这将在下一节中讨论。gydF4y2Ba

通过考虑Eq. (gydF4y2Ba28gydF4y2Ba)，则SMR衰减率为gydF4y2Ba\ (\ kappa _{一}= 1.5 \伽马\)gydF4y2Ba，已知模态gydF4y2Ba一个gydF4y2Ba总是在我们感兴趣的区域的强量子位- smr耦合体系中。的rabi型振荡gydF4y2Ba\ (g ^ {(2)} (0) \)gydF4y2Ba发生在SMR模式下gydF4y2Ba一个gydF4y2Ba混合模式gydF4y2BacgydF4y2Ba．在无花果。gydF4y2Ba3.gydF4y2BaA，弱耦合区和强耦合区分别对应于gydF4y2BaggydF4y2Ba小于或大于整个系统的最大衰减率。gydF4y2Ba

给定Eq. (gydF4y2Ba28gydF4y2Ba)，我们处于“好腔”制度gydF4y2Ba^71gydF4y2Ba,因为gydF4y2Ba\(\kappa _{a}<\{\kappa _b,g,f\}\)gydF4y2Ba．在范围内gydF4y2Ba\(g/2\pi \in (4.5,42)\)gydF4y2BaMHz，混合模式gydF4y2BacgydF4y2Ba具有亚泊松统计量，而SMR模在所有显示的情况下都具有超泊松统计量，并且在QD模中声子出现了非常弱的亚泊松统计量gydF4y2BabgydF4y2Ba，但仍然对应于表中的Case 4gydF4y2Ba1gydF4y2Ba．这种行为在b模态下变为超泊松统计量，对应于情形7，如图所示。gydF4y2Ba3.gydF4y2Baa.有模式转换gydF4y2BacgydF4y2Ba从亚泊松统计到超泊松统计，这对应于强耦合状态下从情形7到情形8的转换，其中其他两个模态都是超泊松的。观察gydF4y2Ba\ (g ^ {(2)} (0) > 1 \)gydF4y2Ba见证PIT和这种效应的量子性质将在下面进一步探讨。gydF4y2Ba

为了更好地探测和理解系统在特定参数范围内的动力学，我们还分析了延迟时间二阶光子相关函数，定义为gydF4y2Ba

在哪里gydF4y2Ba\(n_z(t)=z^\dagger (t) z(t)\gydF4y2Ba玻色子数在模态中吗gydF4y2Ba\ (z = a, b, c, d \)gydF4y2Ba，运算符乘积按正常顺序(::)和时间顺序写gydF4y2Ba\ (\ mathscr {T} \)gydF4y2Ba．与gydF4y2Ba\ (g_z ^{(2)}(\τ)\)gydF4y2Ba可以研究另一种量子光数相关现象。具体来说，在光子的情况下，它被称为光子反聚束gydF4y2Ba\ (g ^ {(2)} (0) < g ^{(2)}(\τ)\)gydF4y2Ba，光子解聚ifgydF4y2Ba\(g^{(2)}(0)\近似g^{(2)}(\tau)\)gydF4y2Ba，和光子聚束ifgydF4y2Ba\ (g ^ {(2)} (0) > g ^{(2)}(\τ)\)gydF4y2Ba，通常定义为较短或非常短的延迟时间gydF4y2Ba\ \(τ\)gydF4y2Ba^72gydF4y2Ba．值得注意的是，光子反聚束是在20世纪70年代由金布尔、达格奈斯和曼德尔首次通过实验观察到的gydF4y2Ba^73gydF4y2Ba．这是历史上第一次实验证明了电磁场的量子性质，这与光电聚束不同，不能用经典理论来解释。gydF4y2Ba

类似地，人们也可以研究声子和/或混合模式玻色子的反聚束和聚束。请注意，术语光子反聚束通常可与亚泊松光子数统计互换使用gydF4y2Ba^21gydF4y2Ba．然而，为了避免混淆，我们可以参考单时间(或零延迟时间)光子反聚束，如果定义为gydF4y2Ba\ (g ^ {(2)} (0) \)gydF4y2Ba和两时间(或延迟时间)光子反聚束，如果定义通过gydF4y2Ba\ (g ^{(2)}(\τ)\)gydF4y2Ba．gydF4y2Ba

在无花果。gydF4y2Ba4gydF4y2Ba，我们绘制了gydF4y2Ba\ (g ^{(2)}(\τ)\)gydF4y2Ba的范围[0,1.5]gydF4y2Ba\(g/\kappa _{\max}\)gydF4y2Ba．这个范围也如图所示。gydF4y2Ba3.gydF4y2Baa，其中可以确定情况4和7的示例。正如预期的那样，我们可以在图中看到SMR和混合模式的振荡。gydF4y2Ba4gydF4y2Baa, c,分别。这些振荡是由量子位- smr耦合之间的竞争引起的gydF4y2BaggydF4y2Ba以及SMR-QD跳变gydF4y2BafgydF4y2Ba在我们的系统中。显然，通过分析gydF4y2Ba\ (g ^{(2)}(\τ)\)gydF4y2Ba在弱耦合条件下，振荡频率小于由两种耦合作用引起的强耦合条件下的振荡频率gydF4y2BaggydF4y2Ba而且gydF4y2BafgydF4y2Ba．此外，在一个非常弱的耦合状态下，其中gydF4y2Ba\ (g \我1 \)gydF4y2Ba振荡是由跳变强度引起的gydF4y2BafgydF4y2Ba，用周期表示gydF4y2Ba\[2 \π/ f \)gydF4y2Ba^74gydF4y2Ba．这意味着，在弱耦合状态下，SMR和QD之间的耦合也可以在我们的系统中产生振荡，在这种情况下，振荡的周期是由gydF4y2Ba\ (f = 5.5 \伽马\)gydF4y2Ba，近似等于gydF4y2Ba\(\tau \约0.036\)gydF4y2Ba，与图中推导出的周期相吻合，如图所示。gydF4y2Ba5gydF4y2Bac.这些有害的振荡应该在比SMR寿命更长的时间尺度上被抑制gydF4y2Ba\(\tau =1/\kappa _a\)gydF4y2Ba使玻色子反聚束在我们感兴趣的领域得以存在。gydF4y2Ba

相关效应的各种组合如图所示。gydF4y2Ba5gydF4y2Ba．图中所有面板。gydF4y2Ba5gydF4y2Ba这是光子模式gydF4y2Ba一个gydF4y2Ba是超泊松式的，而混合模式呢gydF4y2BacgydF4y2Ba是亚泊松反聚束的。然而，声子模式的性质gydF4y2BabgydF4y2Ba每个面板都不一样。具体来说，模式gydF4y2BabgydF4y2Ba(a)超poissonian和unbunch[定义为gydF4y2Ba\(g_b^{(2)}(0)\近似g_b^{(2)}(\tau)\)gydF4y2Ba对于非零但较短的延迟时间gydF4y2Ba\ \(τ\)gydF4y2Ba]， (b)泊松的和非聚束的，(c)亚泊松的和非聚束的，(d)超泊松的和聚束的，以及(e)泊松的和聚束的，通常用于非常短的延迟时间gydF4y2Ba\ \(τ\)gydF4y2Ba．请注意，面板(a, b, c)用于smr驱动系统，而其余面板(d, e)用于qd驱动系统，它们将在下一节中详细讨论。gydF4y2Ba

特别地，我们可以看到，通过减少的耦合gydF4y2Ba\ (g / \ kappa _b = 1.1 \)gydF4y2Ba在无花果。gydF4y2Ba5gydF4y2Bab, QD模式gydF4y2BabgydF4y2Ba用泊松统计解串，而混合模式gydF4y2BacgydF4y2Ba展品antibunchinggydF4y2Ba\(g^{(2)}(0) < g^{(2)}(\tau)\)gydF4y2Ba亚泊松统计gydF4y2Ba\ (g ^ {(2)} (0) < 1 \)gydF4y2Ba在这两种情况下。辅助模式的作用gydF4y2BabgydF4y2Ba在某种意义上，是将模态中的超泊松统计量转化为亚泊松统计量gydF4y2BacgydF4y2Ba．gydF4y2Ba

两种模式的互消干涉gydF4y2Ba一个gydF4y2Ba而且gydF4y2BabgydF4y2Ba在平衡线性耦合器处，可以得到混合模态的亚泊松统计量。我们甚至在弱非线性(或弱耦合)体系中观察到这种效应，该体系见证了非常规PB，如“gydF4y2Ba方法gydF4y2Ba”。值得注意的是，在这项研究中，我们的目标是观察gydF4y2Ba\ (g ^{(2)}(\τ)< 1 \)gydF4y2Ba不仅在gydF4y2Ba\ \(τ= 0 \)gydF4y2Ba，但也适用于非零延迟时间(例如，gydF4y2Ba\(\tau \in [0,0.1]\)gydF4y2Ba)中的玻色子反聚束统计数据的标准实验演示，例如，参考文献gydF4y2Ba^{7gydF4y2Ba，gydF4y2Ba75gydF4y2Ba}．因此，图中所示的情况。gydF4y2Ba4gydF4y2Baa,c很难被认为是亚泊松统计的令人信服的证明，因为振荡发生在gydF4y2Ba\ (g_ {a、c} ^{(2)}(\τ)\)gydF4y2Ba随着gydF4y2Ba\ \(τ\)gydF4y2Ba．更令人信服的证明这些影响没有这样的振荡(或通过相当大的抑制它们)在图中展示。gydF4y2Ba6gydF4y2Ba而且gydF4y2Ba7gydF4y2Ba，下一节将详细分析。gydF4y2Ba

解释模态下的超泊松光子数统计和光子聚束gydF4y2Ba一个gydF4y2Ba对于以SMR模式泵送的系统，我们分析图。gydF4y2Ba5gydF4y2Ba一个与gydF4y2Ba\(g\约\kappa _{m}\)gydF4y2Ba关于这些情况下能级的非谐性。gydF4y2Ba

的gydF4y2BaggydF4y2Ba式中的项(gydF4y2Ba2gydF4y2Ba)对应于标准的Jaynes-Cummings模型，具有熟悉的特征值gydF4y2Ba^62gydF4y2Ba：gydF4y2Ba

对应的特征态:gydF4y2Ba

它们通常被称为盛装状态或盛装状态，在哪里gydF4y2Ba\(\theta _n = \ ω _{n} / \ δ _1\)gydF4y2Ba是混合角，gydF4y2Ba\(δ_1 = \ \ _ {q} - \ω_ {_ \ mathrm鼻中隔黏膜下切除术后{}}\)gydF4y2Ba为SMR与量子位之间的失谐。此外,gydF4y2Ba\ \(ω_ {n} = 2 g \√{n + 1} \)gydF4y2Ba可以解释为gydF4y2BangydF4y2Ba-光子拉比频率的共振，所以，特别地，gydF4y2Ba\ \(ω_ {0}= 2 g \)gydF4y2Ba为真空拉比频率。由此可见，能谱明显是非谐波的，这是观测PB的必要条件。注意，Jaynes-Cummings相互作用可以在色散极限(即远共振)中有效地描述为Kerr非线性(详细的推导见，例如，gydF4y2Ba^50gydF4y2Ba)，这是许多PB效应预测中假设的标准非线性。gydF4y2Ba

为了证明完全哈密顿量的非调和能级gydF4y2Ba\ (H_ {+} \)gydF4y2Ba谐振(见图。gydF4y2Ba2gydF4y2Ba)时，我们假设驱动器耦合强度较弱gydF4y2Ba\(η_{一}\ \)gydF4y2Ba．因此，系统希尔伯特空间可以被截断。我们假设在弱驱动状态下，极化子数最多等于2。基态是gydF4y2Ba\(| \psi _0 \rangle =| 0,0,g \rangle\)gydF4y2Ba对应的特征值gydF4y2Ba\ (E_0 = 0 \)gydF4y2Ba．第一个流形的三个特征值(特征态包含一个极化子)，如图所示。gydF4y2Ba2gydF4y2Bab:gydF4y2Ba

而第二个流形的五个本征值(本征态包含两个极化元)，如图所示。gydF4y2Ba2gydF4y2Bac,写道:gydF4y2Ba

在哪里gydF4y2Ba\ (f = \√6 {3 f ^ 2 (10 g ^ 2 + 3 f ^ 2) + g ^ 4} \)gydF4y2Ba．特别是通过假设gydF4y2Ba\ (f = 5 \伽马\)gydF4y2Ba而且gydF4y2Ba\ (g = 7.5 \伽马\)gydF4y2Ba时，第一流形和第二流形的特征能分别为:(1)gydF4y2Ba\三角洲(\ \)gydF4y2Ba，gydF4y2Ba\(\Delta \pm 9.01388\gamma\约\Delta \pm 9\gamma\)gydF4y2Ba，和(2)gydF4y2Ba\[2 \三角洲\)gydF4y2Ba，gydF4y2Ba\(2\Delta \pm 5.82965\gamma\约2\Delta \pm 6\gamma\)gydF4y2Ba,gydF4y2Ba\(2\Delta \pm 16.11725\gamma\约2\Delta \pm 16\gamma\)gydF4y2Ba．gydF4y2Ba

探测抽运模式的一个简单方法是记录二阶相关gydF4y2Ba\ (g ^ {(2)} (0) \)gydF4y2Ba作为函数gydF4y2Ba\ \(δ_ {_ \ mathrm鼻中隔黏膜下切除术后{}}\)gydF4y2Ba，其中泵频gydF4y2Ba\ω_p (\ \)gydF4y2Ba的变化(见图。gydF4y2Ba8gydF4y2Ba)．为了做到这一点，我们首先考虑共振情况为gydF4y2Ba\ \(ω_ {_ \ mathrm鼻中隔黏膜下切除术后{}}_ {m} = \ω= \ _q =ω\ \)gydF4y2Ba式中(gydF4y2Ba8gydF4y2Ba),gydF4y2Ba\(\ ω -\ ω _p=\Delta\)gydF4y2Ba．如图所示。gydF4y2Ba8gydF4y2BaA中可以看到局部极小值为负值gydF4y2Ba\ (\ log g ^ {(2)} (0) \)gydF4y2Ba为三种模式，即表中的情形1gydF4y2Ba1gydF4y2Ba,在gydF4y2Ba\(\Delta _{_\ mathm {SMR}}/\gamma =\pm 9\)gydF4y2Ba，对应于gydF4y2Ba\(\Delta =\pm \√{g^2+f^2}\ pm 9\gamma\)gydF4y2Ba，则式为(gydF4y2Ba17gydF4y2Ba)．这意味着泵浦频率位于两个有能量的装扮态gydF4y2Ba\ (E ^ {(1)} _1 \)gydF4y2Ba而且gydF4y2Ba\ (E ^ {(1)} _3 \)gydF4y2Ba．我们从第二个能量流形中脱离共振，这意味着在这些频率上观测PB的可能性。gydF4y2Ba

此外，我们的模拟预测的最大值gydF4y2Ba\(\log g^{(2)}(0)\约3\)gydF4y2Ba在三种模态下显示出很强的超泊松统计量(对应于表中的情形8gydF4y2Ba1gydF4y2Ba),gydF4y2Ba\(\Delta _{_\mathrm{SMR}} \rightarrow 0\)gydF4y2Ba．特别是在gydF4y2Ba\(\Delta _{_\ mathm {SMR}}/\gamma \约\pm 6\)gydF4y2Ba时，泵频率接近gydF4y2Ba\ (E ^{(2)} _1 \大约6 \)gydF4y2Ba而且gydF4y2Ba\ (E ^{(2)} _4 \大约6 \)gydF4y2Ba，分别为第二流形，其中双光子共振的概率最大，作为PIT的签名。它表示泵是在共振的一个级别在混合动力系统的能量级别的第二个歧管，在这里明确gydF4y2Ba\ (E ^ {(2)} _1 \)gydF4y2Ba而且gydF4y2Ba\ (E ^ {(2)} _4 \)gydF4y2Ba．从图中可以看出。gydF4y2Ba8gydF4y2Ba的峰值(分析范围内的全局极大值)gydF4y2Ba\ (\ log g_n ^ {(2)} (0) > 0 \)gydF4y2Ba为gydF4y2Ba\ (n = a, b, c \)gydF4y2Ba在gydF4y2Ba\ \(δ_ {_ \ mathrm鼻中隔黏膜下切除术后{}}= 0 \)gydF4y2Ba．特别地，在这里吸收单个光子的概率减小了。然而，如果一个光子被吸收，它会增强捕获后续光子的概率，这种效应会产生超泊松统计量，这是由于观测到单个光子的概率也非常小的事实(gydF4y2Ba\ (P_ {10 g} \我1 \)gydF4y2Ba)，小于观测到两个光子的概率gydF4y2Ba^{6gydF4y2Ba，gydF4y2Ba76gydF4y2Ba}．gydF4y2Ba

可以看出，通过调整驱动频率到过渡gydF4y2Ba\ (E_2-E_0 \)gydF4y2Ba在整个非线性系统的能谱中，接纳两个光子的概率增加。这导致了超泊松统计量，这是相反的情况下，当驱动频率调整到过渡gydF4y2Ba\ (E_1-E_0 \)gydF4y2Ba，此时吸收后续光子的概率降低，导致PB。gydF4y2Ba

通过假设非共振条件，gydF4y2Ba\ \(ω_ {_ \ mathrm鼻中隔黏膜下切除术后{}}\ ne \ω_ {m} \ ne \ω_q \)gydF4y2Ba，我们在图中表示。gydF4y2Ba8gydF4y2BaB为三种模态的相关函数(gydF4y2Ba一个gydF4y2Ba，gydF4y2BabgydF4y2Ba，gydF4y2BacgydF4y2Ba的函数gydF4y2Ba\ \(δ_ {_ \ mathrm鼻中隔黏膜下切除术后{}}\)gydF4y2Ba在这种情况下，当驱动器在中间被调谐时，混合系统的装扮态本征能。gydF4y2Ba

图中观察到PB和PIT效应。gydF4y2Ba8gydF4y2Ba可以通过考虑一些距离谐振距离的度量来解释，如图所示。gydF4y2Ba9gydF4y2Baa.单光子共振、双光子共振和三光子共振(PRs)的距离分别定义为:gydF4y2Ba

在哪里gydF4y2Ba\ω_p (\ \)gydF4y2Ba是泵的频率，它与混合动力系统的能量有关。在这里gydF4y2Ba\ \(ω^ {(n)} _i \)gydF4y2Ba频率(标记下标?gydF4y2Ba我gydF4y2Ba)在gydF4y2Ba\ (n \ hbox {th} \)gydF4y2Ba流形，所以最小化被重复执行gydF4y2Ba\ \(ω^ {(n)} _i \)gydF4y2Ba对于一个给定的流形gydF4y2BangydF4y2Ba．数字gydF4y2Ba9gydF4y2Ba显示了共振距离gydF4y2Ba\ \(δ_ {_ \ mathrm鼻中隔黏膜下切除术后{}}\)gydF4y2Ba,在那里gydF4y2Ba\ω_p (\ \)gydF4y2Ba对整个系统的能量进行了调整。下降gydF4y2Ba\ (g ^ {(2)} (0) \)gydF4y2Ba在gydF4y2Ba\(\Delta _{_\ mathm {SMR}}/\gamma =10\)gydF4y2Ba(见图。gydF4y2Ba8gydF4y2Bab)，这是PB的特征，对应于单一激发的共振，从gydF4y2Ba\ (D_ \ mathrm{1公关}\)gydF4y2Ba，并且在该频率下较高的激励下是非共振的(见图。gydF4y2Ba9gydF4y2Baa).二阶相关函数gydF4y2Ba\ (g ^ {(2)} _c (0) \)gydF4y2Ba由于混合模式有一个下降作为PB周围的标志gydF4y2Ba\(\Delta _{_\ mathm {SMR}}/\gamma =-3.4\)gydF4y2Ba，而模态gydF4y2Ba一个gydF4y2Ba而且gydF4y2BabgydF4y2Ba显示超泊松统计量(表示PIT)，如图所示。gydF4y2Ba8gydF4y2Bab.这种效应可以通过温度的下降来证明gydF4y2Ba\ (D_ \ mathrm{1公关}\)gydF4y2Ba它是非共振的gydF4y2Ba\ (D_ \ mathrm{2公关}\)gydF4y2Ba而且gydF4y2Ba\ (D_ \ mathrm{3公关}\)gydF4y2Ba，如图所示。gydF4y2Ba9gydF4y2BaA，而模态gydF4y2Ba一个gydF4y2Ba而且gydF4y2BabgydF4y2Ba表现出坑。下面将进一步讨论这种非常规PB类型。gydF4y2Ba

通过减少gydF4y2Ba\ \(δ_ {_ \ mathrm鼻中隔黏膜下切除术后{}}/γ\ \)gydF4y2Ba从0到−2，相关函数gydF4y2Ba\ (g ^ {(2)} _a (0) \)gydF4y2Ba为图中的SMR模式。gydF4y2Ba8gydF4y2BaA在形状上类似于肩膀。我们在这个点或区域观察到PIT，正如我们在图中的共振距离图中的发现所预期的那样。gydF4y2Ba9gydF4y2Baa.的确，有一个下降gydF4y2Ba\ (D_ \ mathrm{2公关}\)gydF4y2Ba在这一点上有更高的共振，这解释了PIT的发生。gydF4y2Ba

现在让我们考虑一下gydF4y2Ba\(\Delta _{_\mathrm{SMR}}/\gamma \rightarrow 3\)gydF4y2Ba在无花果。gydF4y2Ba8gydF4y2BaB表示与量子比特共振的泵浦频率，gydF4y2Ba\δ_q = 0 (\ \)gydF4y2Ba，这接近于混合模态的共振频率。在这种情况下，多光子跃迁被诱导，从而导致PIT在gydF4y2Ba\(\Delta _{_\ mathm {SMR}}/\gamma =3\)gydF4y2Ba，我们观察到gydF4y2Ba\ (\ log g ^ {(2)} (0) > 0 \)gydF4y2Ba在图中的这个频率。gydF4y2Ba8gydF4y2Bab.显然，我们在这里与更高的能级共振，而驱动强度非常小，gydF4y2Ba\(\eta _{a}/\gamma =0.7\)gydF4y2Ba．观测到单个光子的概率也和峰值一样小gydF4y2Ba\(\Delta _c= 0\)gydF4y2Ba，但如果单个光子被吸收，那么捕获后续光子的概率就会增加，就像PIT一样。gydF4y2Ba

通过对系统进行优化，得到了系统参数，观测了SMR和QD模式下的超泊松统计量。在亚泊松统计区gydF4y2Ba\ (g ^ {(2)} (0) \)gydF4y2Ba时，可以从图中观察到。gydF4y2Ba14gydF4y2Ba(在“gydF4y2Ba方法gydF4y2Ba”)gydF4y2Ba\ (g ^ {(3)} (0) > 1 \)gydF4y2Ba和/或gydF4y2Ba\ (g ^ {(4)} (0) > 1 \)gydF4y2Ba，它们是高阶光子/声子共振和多重pit(见“gydF4y2Ba方法gydF4y2Ba”)。实际上，通过计算二阶相关函数来见证PB和PIT现象，高阶相关函数可以用来测试给定的效应是否确实是:(1)单PB或单PIT，(2)多PB或多PIT，或(3)这些效应的非标准版本，如“gydF4y2Ba方法gydF4y2Ba和，例如，在参考。gydF4y2Ba^{29gydF4y2Ba，gydF4y2Ba53gydF4y2Ba}．如上所述，这些参数使我们能够在相对较长的延迟时间内实现亚泊松统计。gydF4y2Ba

在本节中，我们分析了稳态玻色子相关效应，包括混合模封锁和PIT，在量子点驱动的耗散系统中，由哈密顿量描述gydF4y2Ba\ (H”\)gydF4y2Ba主方程(gydF4y2Ba12gydF4y2Ba)，以查阅方程式中主要指定的参数。（gydF4y2Ba29gydF4y2Ba)及(gydF4y2Ba30.gydF4y2Ba)．gydF4y2Ba

来消除或至少抑制不希望出现的振荡gydF4y2Ba\ (g ^{(2)}(\τ)\)gydF4y2Ba在本节中，我们假设我们的系统在QD上是经典驱动的。此外，我们假设SMR处于坏腔状态，如gydF4y2Ba\ (\ kappa _ {_ \ mathrm鼻中隔黏膜下切除术后{}}\ gg g ^ 2 / \ kappa _ {_ \ mathrm鼻中隔黏膜下切除术后{}}\ gg \伽马\)gydF4y2Ba^71gydF4y2Ba．因此，我们将有效系统哈密顿量应用于旋转架，如Eq. (gydF4y2Ba9gydF4y2Ba)．即使一辈子gydF4y2Ba\ \(τ_ {_ \ mathrm鼻中隔黏膜下切除术后{}}= 1 / \ kappa _ {_ \ mathrm鼻中隔黏膜下切除术后{}}\)gydF4y2Ba的时间比在SMR驱动系统中假设的时间短得多，这在前一节中讨论过，混合模式，如下所示，在相当长的延迟时间内没有振荡，这是由于驱动QD。gydF4y2Ba

为了研究系统的玻色子数统计量，我们计算了二阶相关函数gydF4y2Ba\ (g ^ {(2)} (0) \)gydF4y2Ba为优化参数，这使我们能够演示表中的情况4、6和7gydF4y2Ba1gydF4y2Ba在无花果。gydF4y2Ba3.gydF4y2Bab.在情形7中，也就是我们特别感兴趣的，模态gydF4y2Ba一个gydF4y2Ba而且gydF4y2BabgydF4y2Ba都是超泊松的，比如gydF4y2Ba\ (\ log g ^ {(2)} (0) > 0 \)gydF4y2Ba，而混合模式gydF4y2BacgydF4y2Ba是亚泊松的，如gydF4y2Ba\ (\ log g_c ^ {(2)} (0) < 0 \)gydF4y2Ba．通过增加耦合gydF4y2BaggydF4y2BaSMR和量子位之间，即模式gydF4y2BabgydF4y2Ba由于受到模态非线性的影响，变为亚泊松态gydF4y2Ba一个gydF4y2Ba．gydF4y2Ba

为了检验PB的第二个准则，二阶相关函数gydF4y2Ba\ (g ^{(2)}(\τ)\)gydF4y2Ba考虑如下。数字gydF4y2Ba6gydF4y2Ba显示gydF4y2Ba\ (g ^{(2)}(\τ)\)gydF4y2Ba对应于gydF4y2Ba\ (g ^ {(2)} (0) \)gydF4y2Ba图。gydF4y2Ba3.gydF4y2Bab显示情形4、6和7。如图所示，在混合模式下观察到玻色子反聚束现象。gydF4y2Ba6gydF4y2Bac，而SMR模式显示聚束，如图所示。gydF4y2Ba6gydF4y2Baa.此外，声子反聚束和聚束，除了解聚束[即，gydF4y2Ba\(g_b^{(2)}(0)\近似g_b^{(2)}(\tau)\)gydF4y2Ba为gydF4y2Ba\(\tau \gtrapprox 0\)gydF4y2Ba]，在QD模态的研究区域观察到，如图所示。gydF4y2Ba6gydF4y2Bab.从图中可以清楚地看出。gydF4y2Ba6gydF4y2Ba三种模式下玻色子的反聚束存在于某些特定的耦合体系中(大约gydF4y2Ba\ (g = 0.7 \ kappa _m \)gydF4y2Ba)相对较长的延迟时间gydF4y2Ba\(\tau > 1/\kappa\)gydF4y2Ba和振荡gydF4y2Ba\ (g_c ^{(2)}(\τ)\)gydF4y2Ba在混合模式中不存在gydF4y2BacgydF4y2Ba．此外，观察到玻色子聚束，当gydF4y2Ba\ (g_a ^{(2)}(\τ)\)gydF4y2Ba当延迟时间大于腔光子寿命时，衰减迅速，如图所示。gydF4y2Ba5gydF4y2Bad, e。gydF4y2Ba

理解混合模式的时延依赖关系gydF4y2BacgydF4y2Ba时，我们考虑Eq. (gydF4y2Ba9gydF4y2Ba)，当SMR、QD和量子位的共振频率相同时，gydF4y2Ba\ \(ω_ {_ \ mathrm鼻中隔黏膜下切除术后{}}_ {m} = \ω= \ _q =ω\ \)gydF4y2Ba而且gydF4y2Ba\ (g = 4.5 \伽马\)gydF4y2Ba．如图所示。gydF4y2Ba10gydF4y2BaA，有三个下降(局部最小值)gydF4y2Ba\ (g ^ {(2)} _b (0) < 0 \)gydF4y2Ba对于模式gydF4y2BabgydF4y2Ba我们假设的量子点gydF4y2Ba\(g<\min \{\kappa _a， \kappa _b\}\)gydF4y2Ba而且gydF4y2Ba\ (f > g \)gydF4y2Ba．对于这些参数，模态只产生了一个弱非线性gydF4y2BabgydF4y2Ba．因此，能级的非谐性不能解释在这三个倾角处观测到的PB效应(见图)。gydF4y2Ba9gydF4y2Bab).实际上，这些下降gydF4y2Ba\ (\ log g ^ {(2)} _b (0) \)gydF4y2Ba是由于单光子共振跃迁，这对应于非常规的PB，如解释非厄米有效哈密顿方法在下一节和“gydF4y2Ba方法gydF4y2Ba”。gydF4y2Ba

数字gydF4y2Ba10gydF4y2Bac显示gydF4y2Ba\ (\ log g_i ^ {(2)} (0) \)gydF4y2Ba对于三个模态的函数gydF4y2Ba\ \(δ_ {_ \ mathrm鼻中隔黏膜下切除术后{}}\)gydF4y2Ba．在这种情况下，我们假设SMR、QD和量子比特的共振频率不相同，并且每个模式的失谐相对于gydF4y2Ba\ω_p (\ \)gydF4y2Ba是不同的。这表明，当gydF4y2Ba\(\Delta _{_\ mathm {SMR}}/\gamma \rightarrow 2\)gydF4y2Ba在该模式下，可以诱导多光子跃迁(以及PIT或多pb)gydF4y2Ba一个gydF4y2Ba，其中泵浦频率在与量子比特的共振中，gydF4y2Ba\(\ ω _p=\ ω _q\)gydF4y2Ba．这种效应如图所示。gydF4y2Ba14gydF4y2Ba(在“gydF4y2Ba方法gydF4y2Ba)对应于高阶矩的局部最大值gydF4y2Ba\ (g_{我}^ {(3)}(0)\)gydF4y2Ba而且gydF4y2Ba\ (g_{我}^ {(4)}(0)\)gydF4y2Ba．同样，共振情况下，模式中的非常规PBgydF4y2BabgydF4y2Ba而且gydF4y2BacgydF4y2Ba可以在下一节中应用的方法来解释。gydF4y2Ba

在无花果。gydF4y2Ba11gydF4y2Ba，我们研究了二阶相关函数如何揭示PIT状态，对应于表中的Case 8gydF4y2Ba1gydF4y2Ba，作为smr泵强度的函数gydF4y2Ba\(η_a \ \)gydF4y2Ba[在图(a)和(c)中]和qd泵强度gydF4y2Ba\(η_b \ \)gydF4y2Ba[在第(b)及(d)栏内]。混合模式gydF4y2BacgydF4y2Ba为所有所示情况和泵强度的超泊松。模式gydF4y2Ba一个gydF4y2Ba而且gydF4y2BabgydF4y2Ba都是超泊松的[除了模态gydF4y2Ba一个gydF4y2Ba图(b)]用于小泵强度gydF4y2Ba\ \(η_ {a、b} \)gydF4y2Ba．通过将驱动功率至少增加到某些值，这些值可以在特定模式的图中识别出来，我们观察到相关函数gydF4y2Ba\ (g ^ {(2)} (0) \)gydF4y2Ba也为所有模式(除了上述情况)减少。这一性质根据Ref的“真”PIT的附加判据，证实了混合系统中预测的PIT的非经典性。gydF4y2Ba^14gydF4y2Ba．gydF4y2Ba

在本节中，我们应用参考文献的分析数学形式主义。gydF4y2Ba^45gydF4y2Ba，基于一个非厄米哈密顿量，识别负责诱导非常规PB的量子干涉效应，即弱耦合区或弱非线性区强亚泊松统计量。我们强调这是一种近似的方法，其中量子跳跃的影响被忽略了gydF4y2Ba^{77gydF4y2Ba，gydF4y2Ba78gydF4y2Ba}．gydF4y2Ba

通过考虑前一节所研究的系统在弱泵浦条件下，我们可以截断模式的希尔伯特空间gydF4y2Ba一个gydF4y2Ba而且gydF4y2BabgydF4y2Ba量子比特在两种激发下的总和。这允许我们考虑维的全系统希尔伯特空间gydF4y2Ba\(3\ * 3\ * 2=18\)gydF4y2Ba．此外，弱泵工况意味着gydF4y2Ba\ (C_ {00 g} \ gg C_ {10 g}, C_ {01 g}, C_ {00 e} \ gg C_ {11 g}, C_ e {10}, C_ {01 e}, C_}{20克、C_ {02 g} \)gydF4y2Ba．因此，耦合系统的稳态可以表示为gydF4y2Ba

在哪里gydF4y2Ba\(| n_a,n_b,g/e \rangle\)gydF4y2Ba福克国家在哪里gydF4y2Ba\ (n_a \)gydF4y2BaSMR中的光子，gydF4y2Ba\ (n_b \)gydF4y2Ba量子d中的声子，以及较低的(gydF4y2Ba\(| g \rangle\)gydF4y2Ba)或以上(gydF4y2Ba\(| e\ rangle\)gydF4y2Ba)量子比特的状态。系统的有效非厄米哈密顿量可以写成gydF4y2Ba

在哪里gydF4y2Ba\ (H”\)gydF4y2Ba由式给出(gydF4y2Ba9gydF4y2Ba)．类似地，我们可以考虑非厄米哈密顿量gydF4y2Ba\ (H \)gydF4y2Ba，由式(gydF4y2Ba8gydF4y2Ba)．gydF4y2Ba

在弱泵浦态下，SMR和QD中光子和声子的平均数量可以近似为gydF4y2Ba\(\langle n_a\rangle \约| C_{10g}|^2\)gydF4y2Ba而且gydF4y2Ba\(\langle n_b\rangle \约| C_{01g}|^2\)gydF4y2Ba,分别。如在“gydF4y2Ba方法gydF4y2Ba，在相同弱泵浦条件下，所产生的光子和声子的二阶相关函数为:gydF4y2Ba

叠加系数在哪里gydF4y2Ba\ (C_ {n, m g} \)gydF4y2Ba式中给出。（gydF4y2Ba39gydF4y2Ba)及(gydF4y2Ba41gydF4y2Ba)．gydF4y2Ba

混合光子-声子模式，定义于式(gydF4y2Ba10gydF4y2Ba)，为输入为SMR和QD模式的平衡线性耦合器的输出模式。如“gydF4y2Ba方法gydF4y2Ba，我们发现，与Eq. (gydF4y2Ba22gydF4y2Ba)，为混合模式的二阶相关函数gydF4y2BacgydF4y2Ba写着:gydF4y2Ba

叠加系数在哪里gydF4y2Ba\ (C ' _ {n m e / g} \)gydF4y2Ba式中给出。（gydF4y2Ba40gydF4y2Ba)及(gydF4y2Ba41gydF4y2Ba)，以及式(gydF4y2Ba34gydF4y2Ba)．gydF4y2Ba

这种方法使我们能够解释混合系统中产生的非常规PB，这是破坏性量子干涉效应的结果，与其他条件一起，确保在SMR和QD中拥有两个光子的概率振幅可以忽略不计。该方法还可以用来寻找一些最优参数来观察系统中的PB。gydF4y2Ba

数字gydF4y2Ba12gydF4y2Ba给出了我们基于Eq.(中主方程的精确数值解的预测的比较。gydF4y2Ba12gydF4y2Ba)，以细曲线表示，并由公式计算。（gydF4y2Ba22gydF4y2Ba)及(gydF4y2Ba23gydF4y2Ba)使用非厄米哈密顿方法，如粗曲线所示。根据这两种形式，相关函数的极大值和极小值的位置是相似的。然而，这些极值可以有更明显的差异，特别是在模态的亚泊松统计中的两个全局最小值gydF4y2BabgydF4y2Ba模态的超泊松最大值gydF4y2Ba一个gydF4y2Ba．这种差异来自于量子跳变的影响，它被恰当地包含在主方程方法中，而在非厄米哈密顿方法中完全被忽略(图2)。gydF4y2Ba12gydF4y2Ba)．gydF4y2Ba

玻色子场的亚泊松统计，如gydF4y2Ba\ (g ^{(2)}(0) \我1 \)gydF4y2Ba，并不是观察“真正”PB的充分标准，它可以是一个好的单光子或单声子源。事实上，其他的标准，比如玻色子反聚束，gydF4y2Ba\(g^{(2)}(0)< g^{(2)}(\tau)\)gydF4y2Ba，高阶相关函数的亚泊松统计量，gydF4y2Ba\ (g ^ {(n)}(0) \我1 \)gydF4y2Ba，亦应满意(详见“gydF4y2Ba方法gydF4y2Ba”)。无论如何，大多数关于PB的研究，特别是关于非常规PB的研究，都局限于对所描述的二阶亚泊松统计量的检验gydF4y2Ba\ (g ^ {(2)} (0) < 1 \)gydF4y2Ba．gydF4y2Ba

正如参考文献中明确讨论的那样。gydF4y2Ba^{21gydF4y2Ba，gydF4y2Ba72gydF4y2Ba，gydF4y2Ba79gydF4y2Ba，gydF4y2Ba80gydF4y2Ba}，光子反聚束和亚泊松统计是不同的光子数相关效应。所以，表中列出的四种情况gydF4y2Ba2gydF4y2Ba，可视为不同类型的PB和PIT。我们表明，所有这些效应都可以在所研究的系统中观察到。为简洁起见，表gydF4y2Ba2gydF4y2Ba仅限于声子效应。在情况I中定义的PB，通常被称为“真正的”PB，可以是一个很好的单光子源;但是，如上所述，还应该满足其他更高阶的标准。gydF4y2Ba

为了显示这四种不同的效果，我们使用式中设置的参数(gydF4y2Ba30.gydF4y2Ba),gydF4y2Ba\(\kappa _{b} \ll \kappa _{a}\)gydF4y2Ba在gydF4y2Ba\(\kappa _b=0.002\， \gamma\)gydF4y2Ba，表示质量因子为gydF4y2BaQ \ \(大约200年,\)gydF4y2Ba所以gydF4y2Ba\(\eta _{b}/\kappa _{b}\约100\)gydF4y2Ba在强泵驱动的情况下采用QD模式gydF4y2Ba\(\eta _{b}=0.22\， \gamma\)gydF4y2Ba．除了前面提到的现象，如在SMR和QD模式中观察到超泊松统计和聚束，而在混合模式中观察到亚泊松统计和玻色子反聚束，我们在模式中发现了四种类型的PB/PITgydF4y2BabgydF4y2Ba，如表所示gydF4y2Ba2gydF4y2Ba的具体实验可行值的例子gydF4y2Ba\ (g / \ kappa _ {} \)gydF4y2Ba．gydF4y2Ba

情况I对应于更强形式的PB，我们称之为“真正的”PB，当玻色子的非经典性质被它们的反聚束和亚泊松统计所揭示。情形II对应于一种更强的PIT形式，它可以被称为“真正的”PIT，当玻色子同时表现出经典效应:超泊松统计和聚束。在情形III中，我们可以讨论一种较弱的PIT形式，或者等效地，另一种较弱的PB类型，因为这样的玻色子以经典的超泊松统计为特征，它们的非经典性质由反聚束揭示。情形IV代表了PB或PIT的另一种较弱形式，其特征是经典束状玻色子的非经典亚泊松统计。这些结果意味着我们不能笼统地说玻色子的反聚束导致了它们的亚泊松统计量，反之亦然gydF4y2Ba^{21gydF4y2Ba，gydF4y2Ba79gydF4y2Ba}．gydF4y2Ba

因此,gydF4y2Ba\ (g ^{(2)}(\τ)> g ^ {(2)} (0) \)gydF4y2Ba并不一定意味着gydF4y2Ba\ (g ^ {(2)} (0) < 1, \)gydF4y2Ba如图3所示。gydF4y2Ba7gydF4y2Bac、f。此外，作为与情形IV相关的另一个例子，让我们考虑福克状态gydF4y2Ba\(| n \rangle\)gydF4y2Ba与gydF4y2Ba\ (n \通用电气2 \)gydF4y2Ba，为此gydF4y2Ba\ (g ^ {(2)} (0) = 1 - 1 / n \)gydF4y2Ba，这样如果gydF4y2Ba\ (n = 2 \)gydF4y2Ba然后gydF4y2Ba\ (g ^ {(2)} (0) = 0.5, \)gydF4y2Ba所以gydF4y2Ba\ (g ^ {(2)} (0) < 1 \)gydF4y2Ba它并没有伴随玻色子反聚束，在这种情况下是聚束。gydF4y2Ba

本文的重点是混合模式下PB的生成，而其他两种模式都表现为PIT。注意，这是Table的一个非常特殊的情况gydF4y2Ba1gydF4y2Ba，这表明在模态中存在8种玻色子数的组合相关现象gydF4y2Ba一个gydF4y2Ba，gydF4y2BabgydF4y2Ba,gydF4y2BacgydF4y2Ba可以在我们的系统中生成，如表gydF4y2Ba1gydF4y2Ba．因此，我们找到了公式中指定的参数在混合系统中PIT和PB效应的所有8种可能组合。（gydF4y2Ba28gydF4y2Ba), (gydF4y2Ba29gydF4y2Ba)，及(gydF4y2Ba30.gydF4y2Ba)．gydF4y2Ba

在这里，我们描述了测量混合光子-声子模式的强度自相关函数的两种检测方案gydF4y2BacgydF4y2Ba而且gydF4y2BadgydF4y2Ba，如图所示。gydF4y2Ba13gydF4y2Ba．gydF4y2Ba

测量gydF4y2Ba\ (g ^{2}(\τ)\)gydF4y2Ba对于光子模式gydF4y2Ba一个gydF4y2Ba声子模式gydF4y2BabgydF4y2Ba是相当标准的，通常是基于Hanbury-Brown and Twiss (HBT)光学干涉测量法及其声子的广义版本gydF4y2Ba^81gydF4y2Ba,分别。然而，测量gydF4y2Ba米gydF4y2Ba(如图所示。gydF4y2Ba13gydF4y2Ba一个)的gydF4y2Ba\ (g ^{(2)}(\τ)\)gydF4y2Ba，甚至gydF4y2Ba\ (g ^ {(2)} (0) \)gydF4y2Ba，表示光子-声子混合模式gydF4y2BacgydF4y2Ba而且gydF4y2BadgydF4y2Ba如果直接应用是相当具有挑战性的。这里我们提出了两种检测方法，如图所示。gydF4y2Ba13gydF4y2BaB,c，表示间接测量gydF4y2Ba\ (g_ {c, d} ^ {(2)} (0) \)gydF4y2Ba．gydF4y2Ba

测量单元的第一次操作gydF4y2Ba米gydF4y2Ba在两种方案中都是混合模式的线性耦合器变换(gydF4y2BacgydF4y2Ba，gydF4y2BadgydF4y2Ba)gydF4y2Ba\ ((a, b) \)gydF4y2Ba，假设过程是完美的，它应该等于原来的纯光子(gydF4y2Ba一个gydF4y2Ba)和声子(gydF4y2BabgydF4y2Ba)模式。gydF4y2Ba

我们考虑一个线性耦合器(形式上等价于分束器)用一个幺正运算来描述gydF4y2Ba\ (U_ \ mathrm {LC}θ)(\ \)gydF4y2Ba，它转换输入操作符gydF4y2Ba一个gydF4y2Ba而且gydF4y2BabgydF4y2Ba成:gydF4y2Ba

对于实参数gydF4y2Ba\θ(\ \)gydF4y2Ba,在那里gydF4y2Ba\ (T = \ cosθ^ 2 \ \)gydF4y2Ba而且gydF4y2Ba\ (R = 1 - t = \ sinθ^ 2 \ \)gydF4y2Ba分别为线性耦合器的透射系数和反射系数。所研究的混合模态是式的特例。gydF4y2Ba24gydF4y2Ba)gydF4y2Ba\(c\等值c(\theta =\pi /4)\)gydF4y2Ba而且gydF4y2Ba\(d\equiv d(\theta =\pi /4)\)gydF4y2Ba．很明显，第一个变换gydF4y2Ba\ (U_ \ mathrm {LC}(- \π/ 4)\)gydF4y2Ba在无花果。gydF4y2Ba13gydF4y2Bab c是图中变换的逆。gydF4y2Ba13gydF4y2Ba一个。gydF4y2Ba

检测方法1基于测量光子和声子gydF4y2Ba

相关函数gydF4y2Ba\ (g_ {c, d} ^ {(2)} (0) \)gydF4y2Ba在混合光子-声子模式中可以间接测量，如图所示。gydF4y2Ba13gydF4y2BaB，通过测量可观测数据:gydF4y2Ba

在哪里gydF4y2Ba\ (k, l, m, n = 0, 1, 2 \)gydF4y2Ba，利用关系式:gydF4y2Ba

和混合模态的类似关系gydF4y2BadgydF4y2Ba．计量单位gydF4y2Ba\ (M ' _a \)gydF4y2Ba而且gydF4y2Ba\ (M ' _b \)gydF4y2Ba如图2所示。gydF4y2Ba13gydF4y2BaB，分别描述光子和声子的测量。可见，用这种方法来确定gydF4y2Ba\ (g_ {c, d} ^ {(2)} (0) \)gydF4y2Ba，我们必须测量以下可观察的数据:gydF4y2Ba\ (f {01} \)gydF4y2Ba，gydF4y2Ba\ (f {10} \)gydF4y2Ba，gydF4y2Ba\ (f {11} \)gydF4y2Ba，gydF4y2Ba\ (f {02} \)gydF4y2Ba，gydF4y2Ba\ (f {20} \)gydF4y2Ba，gydF4y2Ba\ (f {12} \)gydF4y2Ba，gydF4y2Ba\ (f {21} \)gydF4y2Ba,gydF4y2Ba\ (f {22} \)gydF4y2Ba．几乎每个可观察到的gydF4y2Ba\ (f {kl} \)gydF4y2Ba是否应该与特定的可观测物同时测量gydF4y2Ba\ (g_ {mn} \)gydF4y2Ba，这可以通过图中的巧合计数逻辑(CCL)单元来实现。gydF4y2Ba13gydF4y2Bab。gydF4y2Ba

测量所有必需的光子可观测物gydF4y2Ba\ (f {kl} \)gydF4y2Ba可以通过使用，例如，基于平衡零差相关测量的Shchukin-Vogel方法来执行gydF4y2Ba^82gydF4y2Ba．根据该方法，将光子信号叠加在具有相干态的本振的平衡分束器上gydF4y2Ba\(| \alpha =|\alpha |\exp (\phi) \rangle\)gydF4y2Ba相位可调gydF4y2Baφ\ (\ \)gydF4y2Ba．可观察到的期望的平均值gydF4y2Ba\ (f {kl} \)gydF4y2Ba对于不同的本振相位，可以通过特定探测器记录的符合计数的线性组合来获得吗gydF4y2Baφ\ (\ \)gydF4y2Ba．这部分方法对应于傅里叶变换。最简单的非平凡的配置，使测量可观测gydF4y2Ba\ (f {10} \)gydF4y2Ba，gydF4y2Ba\ (f {01} \)gydF4y2Ba，gydF4y2Ba\ (f {20} \)gydF4y2Ba,gydF4y2Ba\ (f {02} \)gydF4y2Ba，需要四个探测器和三个平衡的BSs，其中额外的输入端口是空的，即只允许量子真空噪声。通过将四个探测器替换为四个平衡的BSs，在它们的输出处总共有八个探测器，人们可以测量任何可观测到的物体gydF4y2Ba\ (f {kl} \)gydF4y2Ba为gydF4y2Ba\ (le 4 k + l \ \)gydF4y2Ba．这些包括所需的可观测数据gydF4y2Ba\ (f {21} \)gydF4y2Ba，gydF4y2Ba\ (f {12} \)gydF4y2Ba,gydF4y2Ba\ (f {22} \)gydF4y2Ba．当然，是可观察到的gydF4y2Ba\ (f {22} \)gydF4y2Ba可以通过HBT干涉测量法进行更简单的测量。声子可观测的测量gydF4y2Ba\ (g_ {mn} \)gydF4y2Ba只需用平衡声子模式线性耦合器取代平衡的BSs，并使用声子探测器，例如，在参考文献中。gydF4y2Ba^81gydF4y2Ba．双模矩的测量gydF4y2Ba\(\langle f_{kl}g_{mn} \rangle\)gydF4y2Ba是，至少在概念上，一个简单的推广单模方法依赖于适当的巧合在光子和声子探测器。请注意，在参考文献中描述了原始单模方法的多模光学版本。gydF4y2Ba^83gydF4y2Ba．gydF4y2Ba

基于仅测量光子的检测方法2gydF4y2Ba

数字gydF4y2Ba13gydF4y2BaC显示了测量单元的另一种实现gydF4y2Ba米gydF4y2Ba，以确定gydF4y2Ba\ (g_ {c, d} ^ {(2)} (0) \)gydF4y2Ba，甚至gydF4y2Ba\ (g_ {c, d} ^{(2)}(\τ)\)gydF4y2Ba．可以说，这种方法比检测方法1更简单、更有效，因为它仅基于测量光子，并使用标准HBT干涉测量法。我们的方法受到了Ref的启发。gydF4y2Ba^48gydF4y2Ba，其中单模声子阻塞的测量是通过光学方法而不是磁动机技术来描述的，这在参考文献中有描述。gydF4y2Ba^47gydF4y2Ba在那里，声子封锁首次被预测。gydF4y2Ba

我们的测量装置实现了以下三个转换:(1)转换声子模式gydF4y2Ba\ (b \)gydF4y2Ba进入光子模式gydF4y2Ba\ (b \)gydF4y2Ba，(2)混合光学模式gydF4y2Ba\(‘\)gydF4y2Ba而且gydF4y2Ba\ (b \)gydF4y2Ba在平衡的BS上生成模式gydF4y2Ba\ \ (c”)gydF4y2Ba而且gydF4y2Ba\ (d ' \)gydF4y2Ba，在理想情况下，它具有与原始混合光子-声子模式相同的玻色子数统计量gydF4y2BacgydF4y2Ba而且gydF4y2BadgydF4y2Ba；最后，(3)对这两种光模式进行了常规光学HBT干涉测量。在单元(1)中，这种转换对应于一个多级SWAP门，它可以由光子-声子线性耦合器实现gydF4y2Ba\(\theta =\pi /2，\)gydF4y2Ba假设辅助输入模式gydF4y2Ba\ (e ' \)gydF4y2Ba是在光子真空状态下，而输出模式呢gydF4y2Ba\ (e”\)gydF4y2Ba处于声子真空状态。在单元(3)中，平衡BS对光学模式的作用gydF4y2Ba\(‘\)gydF4y2Ba而且gydF4y2Ba\ (b \)gydF4y2Ba在无花果。gydF4y2Ba13gydF4y2BaC对应于平衡线性耦合器在光子(gydF4y2Ba一个gydF4y2Ba)和声子(gydF4y2BabgydF4y2Ba)模式，如图所示。gydF4y2Ba13gydF4y2Ba一个。gydF4y2Ba

很明显，线性耦合器变换gydF4y2Ba\ (U_ \ mathrm {LC}θ)(\ \)gydF4y2Ba不仅应用于模式(gydF4y2Ba一个gydF4y2Ba，gydF4y2BabgydF4y2Ba)，但也适用于其他模式。因此，式(gydF4y2Ba24gydF4y2Ba)应作适当修改，以取代(gydF4y2Ba一个gydF4y2Ba，gydF4y2BabgydF4y2Ba)由(gydF4y2BacgydF4y2Ba，gydF4y2BadgydF4y2Ba)，gydF4y2Ba\ ((e、b) \)gydF4y2Ba,gydF4y2Ba\ ((a, b) \)gydF4y2Ba．为简洁起见，我们省略了它们的明确定义。请注意,gydF4y2Ba\ (U_ \ mathrm {LC}(\π/ 2)\)gydF4y2Ba而且gydF4y2Ba\ (U_ \ mathrm {LC}(\π/ 4)\)gydF4y2Ba分别对应一个多级SWAP门和Hadamard-like门;而图中平衡的BS。gydF4y2Ba13gydF4y2BaC对应于gydF4y2Ba\ (U_ \ mathrm {LC}(\π/ 4)\)gydF4y2Ba．gydF4y2Ba

我们提出了一种新型的玻色子封锁，称为混合光子-声子封锁，它是标准光子和声子封锁效应的推广。我们预测了由光子和声子模式线性耦合得到的混合模式的新效应。我们描述了如何在驱动非线性光力学超导系统中产生和检测混合光子-声子阻塞。具体地说，我们考虑了由线性耦合微波谐振器和机械谐振器组成的系统，其中一个谐振器中插入了超导量子比特。gydF4y2Ba

我们研究了系统中光子、声子和混合模式的玻色子数相关性。通过对稳态二阶相关函数的分析，我们发现了可以观测到四种不同类型的玻色子阻塞和/或玻色子诱导隧穿的系统参数体系。因此，我们表明，在所研究的系统中产生的玻色子可以表现出亚泊松(或超泊松)玻色子数统计，在某些情况下伴随玻色子反聚束，在另一些情况下伴随玻色子聚束。这些结果可以解释为四种不同类型的阻塞或隧道效应，总结在表中gydF4y2Ba2gydF4y2Ba．gydF4y2Ba

通过通过SMR驱动的混合系统的能级调节泵浦频率，我们表明可以观察到PB和PIT，可以用强耦合(或大非线性)体系中的大能级非谐性来解释。然而，二阶相关函数的时间演化gydF4y2Ba\ (g ^{(2)}(\τ)\)gydF4y2Ba由于耦合而振荡gydF4y2BaggydF4y2BaSMR和量子位之间以及跳变gydF4y2BafgydF4y2Ba在SMR和QD之间。我们证明了在混合模式下诱导PB是可能的gydF4y2BacgydF4y2Ba通过驱动QD而不是SMR，可以存活更长的延迟时间。gydF4y2Ba

我们还在忽略量子跳的基础上，使用非厄米哈密顿方法预测了弱耦合(或弱非线性)体系下三种模式下的非常规PB。我们的分析近似预测与我们的精确主方程解(包括量子跳跃)相对较好地一致。gydF4y2Ba

此外，如表所总结gydF4y2Ba1gydF4y2Ba，我们展示了在三种模式下观察PB或PIT的八种不同组合的可能性(gydF4y2Ba一个gydF4y2Ba，gydF4y2BabgydF4y2Ba,gydF4y2BacgydF4y2Ba)在系统的不同耦合状态下。因此，我们特别发现，光子和声子模式中的隧道效应可以通过简单的线性混合导致混合光子-声子封锁效应。gydF4y2Ba

最后，我们讨论了检测混合模相关的两种方法。其中一种方法是通过平衡零差相关测量来测量光子和声子的各种力矩。而另一种方法是基于将混合模式的声子转换为光子，通过使用线性耦合器作为多级SWAP门，然后应用标准光学HBT干涉测量。gydF4y2Ba

我们相信，我们对光子和声子之间相互作用的研究可以导致开发新的实验方法来控制和测试原子-腔-力学极化激元力学系统的量子态。我们希望我们的工作也能刺激量子工程与混合光子-声子模式的研究。gydF4y2Ba

模拟中使用的参数gydF4y2Ba

我们的数字，如标题所示，绘制了由哈密顿量描述的smr驱动耗散系统gydF4y2Ba\ (H \)gydF4y2Ba，由式(gydF4y2Ba8gydF4y2Ba),假设:gydF4y2Ba

以及qd驱动耗散系统的哈密顿量gydF4y2Ba\ (H”\)gydF4y2Ba，由式(gydF4y2Ba9gydF4y2Ba)，假设gydF4y2Ba

或gydF4y2Ba

在哪里gydF4y2Ba\(π\γ= 10 \ \)gydF4y2BaMHz。这些参数的微小修改在图标题中指定。gydF4y2Ba

高阶相关效应gydF4y2Ba

这里我们简要地研究一下gydF4y2Ba\ (k \ hbox {th} \)gydF4y2Ba-阶玻色子数相关函数gydF4y2Ba\ (g_z ^ {(k)} (0) \)gydF4y2Ba，如式(gydF4y2Ba13gydF4y2Ba)gydF4y2Ba\ (k = 3 4 \)gydF4y2Ba与标准二阶函数相比gydF4y2Ba\ (g_z ^ {(2)} (0) \)gydF4y2Ba对于光子(gydF4y2Ba\ \ (z =)gydF4y2Ba)，声子(gydF4y2BabgydF4y2Ba)，以及混合光子-声子(gydF4y2BacgydF4y2Ba)模式。gydF4y2Ba

数字gydF4y2Ba14gydF4y2Ba显示了我们的结果gydF4y2Ba\ (g_z ^ {(3)} (0) \)gydF4y2Ba(虚线曲线)和gydF4y2Ba\ (g_z ^ {(4)} (0) \)gydF4y2Ba(点虚线)相比gydF4y2Ba\ (g_z ^ {(2)} (0) \)gydF4y2Ba(实心曲线)用于gydF4y2Ba\ (z = a, b, c \)gydF4y2Ba在相应的面板中。注意，同样的曲线gydF4y2Ba\ (g_z ^ {(2)} (0) \)gydF4y2Ba也如图所示。gydF4y2Ba10gydF4y2BaA，但我们重复它们，以便更好地与gydF4y2Ba\ (g_z ^ {(3, 4)} (0) \)gydF4y2Ba．可见，八例表gydF4y2Ba1gydF4y2Ba可分为若干子情况取决于gydF4y2Ba\ (g_z ^ {(3)} (0) \)gydF4y2Ba而且gydF4y2Ba\ (g_z ^ {(4)} (0) \)gydF4y2Ba．这种分类相当复杂，原则上包括gydF4y2Ba\ \ (8 ^ 3 = 512)gydF4y2Ba用例。因此，我们提出了另一种非常简化的分类，只对8种情况进行分类，如表所示gydF4y2Ba3.gydF4y2Ba使用辅助函数gydF4y2Ba\ (g_ {234} \)gydF4y2Ba定义为:gydF4y2Ba

特别是gydF4y2Ba\([-,-,-]\)gydF4y2Ba意味着在给定模式下观测到二阶、三阶和四阶亚泊松光子数统计量，这是观测“真”单pb的必要条件。这种情况可以很容易地在图的两个面板中识别出来。gydF4y2Ba14gydF4y2Ba．一个人也可以找到这种情况gydF4y2Ba\([+,+,+]\)gydF4y2Ba，对应于阶数的超泊松统计gydF4y2Ba\ (k = 2 \)gydF4y2Ba， 3和4，这可以解释为，由1、2和3个光子诱导的隧穿。然而，我们也可以发现六种情况中有四种是中间类型，可以解释为非标准类型single-PB和/或single-PIT，在某些情况下可以识别为multi-PBgydF4y2Ba^{11gydF4y2Ba，gydF4y2Ba26gydF4y2Ba，gydF4y2Ba29gydF4y2Ba，gydF4y2Ba30.gydF4y2Ba，gydF4y2Ba53gydF4y2Ba}．然而，这种多pb的详细分类及其解释并不是本文的重点。给出的结果只表明了在我们的系统中产生过多的各种光子-声子相关效应的可能性，这可以通过实验可行参数的高阶相关函数来揭示。gydF4y2Ba

式中的非厄米哈密顿分析方法(gydF4y2Ba21gydF4y2Ba）gydF4y2Ba

这里，我们采用Ref的方法。gydF4y2Ba^45gydF4y2Ba为了推导出系数gydF4y2Ba\ (C_ {n, m k} \)gydF4y2Ba而且gydF4y2Ba\ (C ^ \ ' _ {n, m k} \)gydF4y2Ba为gydF4y2Ba\(n,m \in {0,1,2}\)gydF4y2Ba而且gydF4y2Ba\ (k = e, g \)gydF4y2Ba，出现在等式中。（gydF4y2Ba22gydF4y2Ba)及(gydF4y2Ba23gydF4y2Ba)．gydF4y2Ba

首先，我们回顾平衡线性耦合器(或平衡分束器)变换，这导致Eq. (gydF4y2Ba24gydF4y2Ba)，如果应用到输入的Fock状态gydF4y2Ba\(| n_a, n_b \rangle\)gydF4y2Ba为gydF4y2Bale 2 \ (n_a + n_b \ \)gydF4y2Ba收益率:gydF4y2Ba

对于输入状态gydF4y2Ba\(| \Psi _{abq}(t) \rangle\)gydF4y2Ba，由式(gydF4y2Ba20.gydF4y2Ba)时，平衡线性耦合器的输出状态表示为:gydF4y2Ba

其中叠加系数为:gydF4y2Ba

我们可以计算系数gydF4y2Ba\ (C_ {n_a, n_b, g / e} \)gydF4y2Ba迭代gydF4y2Ba^45gydF4y2Ba．对于单一激励，并假设共振情况gydF4y2Ba\ \(δ_ {_ \ mathrm鼻中隔黏膜下切除术后{}}=δ_ {m} = \ \ _ {q} = \δ\)gydF4y2Ba而且gydF4y2Ba\(\kappa _{a}=\kappa _b=\kappa\)gydF4y2Ba，稳态叠加系数可计算为:gydF4y2Ba

在哪里gydF4y2Ba\(\eta =\eta _b\)gydF4y2Ba，gydF4y2Ba\(\Delta =\ ω _i-\ ω _p\)gydF4y2Ba而且gydF4y2Ba\(\ω_ {_ \ mathrm鼻中隔黏膜下切除术后{}}= \ω_m = \ω_q =ω\ \)gydF4y2Ba．此外，我们假设弱驱动机制。因此，在第一次迭代中，具有多个激励的状态的贡献，例如gydF4y2Ba\ (C_ {01 e} \)gydF4y2Ba，gydF4y2Ba\ (C_ {11 g} \)gydF4y2Ba,……，一个re negligible. From Eq. (35gydF4y2Ba)，通过比较单一激励下的系数，我们可以看到gydF4y2Ba\ (C_ {10 g} \)gydF4y2Ba而且gydF4y2Ba\ (C_ {00 e} \)gydF4y2Ba都比gydF4y2Ba\ (C_ {01 g} \)gydF4y2Ba，因为一个弱泵浦振幅gydF4y2Ba\埃塔(\ \)gydF4y2Ba，它们可以写成gydF4y2Ba

在第二次迭代中，为了包含总共有两个激励的状态，稳态系数可计算为:gydF4y2Ba

在哪里gydF4y2Ba\(\Delta _{\kappa}=\Delta -i\kappa /2\)gydF4y2Ba而且gydF4y2Ba\(\Delta _{\gamma}=\Delta -i\gamma /2\)gydF4y2Ba．从式中可以看出(gydF4y2Ba37gydF4y2Ba)，我们有gydF4y2Ba

为了最小化gydF4y2Ba\ (C_ {02 g} \)gydF4y2Ba的极小化gydF4y2Ba\ (C_ {11 g} \)gydF4y2Ba而且gydF4y2Ba\ (C_ {01 g} \)gydF4y2Ba也是必需的。在整个系统的能量阶梯中直接和间接激励路径之间的破坏性干扰可以使我们最小化gydF4y2Ba\ (C_ {02 g} \)gydF4y2Ba．这就解释了为什么会出现这种现象gydF4y2Ba\ (g_b ^ {(2)} (0) \)gydF4y2Ba在模式中gydF4y2BabgydF4y2Ba，作为PB的签章。如图所示。gydF4y2Ba12gydF4y2Baa，该模式下的最佳PB出现在gydF4y2Ba\(\Delta _{_\ mathm {SMR}}/g=\pm 1.2\)gydF4y2Ba．上述方程使我们得到了系统参数的解析优化条件，使QD模态的亚泊松特性最大化，从而优化了在模态下观测PB的参数gydF4y2BabgydF4y2Ba．给定Eq. (gydF4y2Ba39gydF4y2Ba)用于单励磁和Eq. (gydF4y2Ba41gydF4y2Ba)，由式(gydF4y2Ba37gydF4y2Ba)，我们表明，用该方法计算的二阶相关函数与主方程法都给出了非常相似的预测，如图所示。gydF4y2Ba12gydF4y2Ba，其中粗曲线基于非厄米哈密顿方法计算，细曲线对应于模态的主方程方法gydF4y2Ba一个gydF4y2Ba，gydF4y2BabgydF4y2Ba,gydF4y2BacgydF4y2Ba．gydF4y2Ba

因此我们发现gydF4y2Ba

的收益率gydF4y2Ba

类似地，我们发现gydF4y2Ba

在哪里gydF4y2Ba\ \(δ_ {\ kappa \伽马}= \ \ _ {\ kappa} +δ_{\伽马}\)gydF4y2Ba辅助功能gydF4y2Ba\ (X_n \)gydF4y2Ba读:gydF4y2Ba\(X_1=\Delta _{\kappa \gamma}^2-f^2\)gydF4y2Ba，gydF4y2Ba\ (X_2 = \三角洲_ {\ kappa \伽马}(2 \ _ {\ kappa} + 5 \δ_{\伽马})4 f ^ 2 \)gydF4y2Ba，gydF4y2Ba\ (X_3 = 2 \三角洲_ {\ kappa}(\三角洲_ {\ kappa} ^ 2 - f ^ 2) X_1 \)gydF4y2Ba，gydF4y2Ba左\ (X_4 = \ [3 \ _ {\ kappa} ^ 2 \δ_ {\ kappa \伽马}+ (\ _ {\ kappa} - \δ_{\伽马})f ^ 2 \] g ^ 2 -δ_ {\ kappa} g ^ 4 \ \)gydF4y2Ba，gydF4y2Ba\ (X_5δ_ {\ kappa} ^ 2 = \ \ _{\伽马}- \δ_{\伽马}f ^ 2 -δ_ {\ kappa} \ g ^ 2 \)gydF4y2Ba，gydF4y2Ba\ (X_6 = 3 \三角洲_ {\ kappa} ^ 2 + 4 \ _ {\ kappa} \δ_{\伽马}+ f ^ 2 \)gydF4y2Ba,gydF4y2Ba\ (X_7 = \三角洲_ {\ kappa} (2 ^ 2 - 3 f \ _{\伽马}\δ_ {\ kappa \伽马})\)gydF4y2Ba．这些公式，连同gydF4y2Ba_{20克}\ \ (C”)gydF4y2Ba式中(gydF4y2Ba34gydF4y2Ba)，使我们能够解析地计算方程中的相关函数。（gydF4y2Ba22gydF4y2Ba)及(gydF4y2Ba23gydF4y2Ba)．gydF4y2Ba