简介

层析量词是估计量子态物理性质的常用工具，其过程依赖于量子态的密度矩阵1．光学零差层析成像是相干场态的概率分布与密度算子之间的单调关系2，这使得所有关于量子态的信息都能被提取出来3.，4，5．因此，许多非经典光态可以用光学零差层析成像来表征。光学层析成像是测试任何量子信息处理实现的关键方法6，7．对神经网络量子态进行了理论和实验研究8，分束器模式的最大纠缠态9，问形变相干态10，以及与氮空位中心相关的单电子自旋态11．光学零差层析成像用于分析克尔介质中的复原12．

人工光-物质相互作用的实现受到越来越多的关注13如:超导电路14，15量子点16被困的离子17，以产生有用的非经典效应，如相干、压缩和量子相关性。特别是超导系统，在设计与谐振器相互作用的超导人工量子比特时具有很大的灵活性18．这些系统为人工量子比特和非线性相互作用的大量理论研究打开了大门19．双光子跃迁已经被Goeppert-Mayer预言了20.．这种效应已广泛应用于荧光显微镜21，以及二色激光脉冲22．基于所提出的超导电路在固态器件中实现了双光子量子Rabi模型15．

利用相干态叠加的维格纳层析成像和耦合到波导腔腔谐振器的固定频率超导传输量子比特，研究了在超导电路环境下建立量子计算和信息的潜力23，24，25．最近，超导传输量子比特和两个光子量子比特被用于量子层析成像实验，实现了两个耦合逻辑量子比特的结构26，并演示了两个误差可校正光子量子比特之间的可控相位门27，以及揭示双模腔中的量子相关性28．

量子态的光学零差层析成像分布非常容易受到退相干和耗散资源的影响12由于非经典损耗与退相干效应之间的密切关系。在本文中，我们利用米尔本运动方程研究了所提出的量子比特-谐振器相互作用的动力学，该方程在存在本征退相干的情况下控制了系统的动力学29．本征退相干模型已被用于研究量子信息资源在众多系统中的动态30.，31，32，33．从理论上研究了本征退相干29并在耦合离子量子比特的线性阵列中实现34没有任何与周围环境的显式耦合。这种退相干形式在封闭的量子位谐振器相互作用中起作用。内在退相干导致量子相干性损失而不损失能量。在这种情况下，系统的动力学由米尔本方程描述。其他方法由主方程控制，描述系统-库相互作用(开放量子系统)35，36，这自然会导致退相干，因为进化后信息会立即丢失。内在退相干不同于发生在开放量子系统中的耗散37，38，39与周围环境相互作用。

在各种超导电路中40氮空位中心41，本征退相干过程得到了实际控制。研究了孤立量子系统的内禀退相干时间，发现它与系统大小和无序强度有关34．量子误差检测减少了超导电路中本征退相干的影响42．微腔偏振子凝聚体中的相位相干性43和约瑟夫森量子比特44是由内在退相干过程控制的。

以前，光学零差层析成像的动力学仅限于特定的模型9，12，即忽略退相干和耗散效应的存在。本文研究了超导电路中的光学层析成像和相干动力学。量子比特耦合到谐振腔的共振双光子相互作用，其状态初始化为相干态或相干态的叠加态，模拟了相关的动力学。此外，量子谐振腔失谐和本征退相干对所选系统状态的光学层析分布动力学的影响是本研究的重点。与之前考虑的光学层析成像相比，这里的光学层析成像分布在存在本征退相干的量子比特-谐振器相互作用下进行了探索。

本文的组织结构如下:具有本征退相干模型的量子谐振腔系统节中，给出了具有本征退相干模型的量子比特谐振腔系统的解析解。在“光学层析分布，光学层析动力学节中，所生成的随时间变化的谐振腔状态的光学层析成像分布的动力学被说明。”结论的部分用于总结。

具有本征退相干模型的量子谐振腔系统

我们考虑了一个双光子量子比特谐振腔模型，该模型描述了一个量子比特和一个谐振腔通过双光子跃迁耦合。该模型可以实现为一个超导电路，由一个dc-SQUID和两个相同的结电感耦合到一个超导通量量子位。二次耦合双光子量子比特谐振腔的哈密顿量由(\(\ \百巴= 1)）45

$ $ \开始{对齐}{\帽子{H}} & = \ω_{平方}\离开({\帽子{\ psi}} ^{\匕首}{\帽子{\ psi}} + \压裂{1}{2}\右)+ \压裂{1}{2}\ω_ {q}{\帽子{\σ}}_ {z} - \压裂{\π}{4}\ tan \离开(\压裂{\π\φ_{直流}}{\φ_{0}}\)\压裂{M I_ {p}}{\φ_{0}}\ω_{平方}({\帽子{\ psi}} +{\帽子{\ psi}} ^{\匕首})^{2}{\帽子{\σ}}_ {x}。\{对齐}$ $
(1）

\(φ_{直流}\ \)表示外部应用的静态通量。\(ω_ {q} \ \)，米,\ (I_ p {} \)分别表示量子位squid的频率、互感和持久电流状态。\(ω_{平方}\ \)SQUID模态频率与湮灭算符是否相同{\ \({\帽子psi}} \)．\(| 0 \纠正\)而且\(| 1 \纠正\)是量子比特的基态和激发态。{\ \({\帽子σ}}_ {x} \)而且\({{\帽子{\σ}}}_ {z} \)设计泡利量子比特密度矩阵。在这里，我们关注SC区域，其中耦合强度与量子位和腔的特征频率相比较小，但大于所有的耗散率。在最高法院制度中，反向轮换条款\({\hat{\sigma}}_{-} {\hat{\psi}}^{2} + H.c\)．而且{\ \({\帽子σ}}_ {x}{\帽子{\ psi}} ^{\匕首}{\帽子{\ psi}} \)，以频率旋转\(2\omega _{q} + \omega _{SQ}\)而且\(ω_ {q} \ \)，分别可以被忽略。哈密顿量可以写成45

$ $ \{对齐的开始 } \!\!\!\!\!{\帽子{H}} & =ω\ _{平方}({\帽子{\ psi}} ^{\匕首}{\帽子{\ psi}} +{\帽子{\σ}}_ {z}) + \ ! \ !\frac{\delta}{2} {\hat{\sigma}}_{z}+ \!\!\λ({\帽子{\ psi}} ^{2} | 1 \纠正\ langle 0 0 \纠正\ langle 1 | + | |{\帽子{\ psi}} ^{2 \匕首})。\{对齐}$ $
（2）

\ \(λ= - \压裂{\π}{4}\ tan(\压裂{\π\φ_{直流}}{\φ_{0}})\压裂{M I_ {p}}{\φ_{0}}\ω_{平方}\)．\(\delta =\omega _{q}-2\omega _{SQ}\)表示量子位谐振器失谐，用于非谐振情况\(\delta \ne 0\)．在量子位谐振腔态的跨空间中\ (\ {| \ varpi _{1} \捕杀= | 1,n \捕杀,| \ varpi _{2} \捕杀= | 0 n + 2 \纠正\}\)式的哈密顿量的盛装态(2)由

$ $ \开始{对齐}| S_ {1} ^ {n} \捕杀= \罪\ζ_ {n} | \ varpi _{1} \捕杀+ \因为\ζ_ {n} | \ varpi _{2} \纠正\ nonumber \ \ | S_ {2} ^ {n} \捕杀= \因为\ζ_ {n} | \ varpi _{1} \纠正——罪\ \ζ_ {n} | \ varpi _{2} \捕杀,\{对齐}$ $
（3）

在哪里

$ ${对齐}\ \开始ζ_ {n} & = \罪^{1}\√6{(间{n} + \δ)/ 2间{n}}, \ nonumber \ \间{n} & = \√6{(\ω2 _ {q} \ω_{平方})^{2}+ \λ^ {2}(n + 1) (n + 2)}。\{对齐}$ $
（4）

能量特征值有如下表达式

$ $ \{对齐}开始V ^ {n} _{1} & =ω\ _{平方}(n + 2) +间{n} \ nonumber \ \ V ^ {n} _{2} & =ω\ _{平方}(n + 2)间的{n}。\{对齐}$ $
（5）

基态能量\(| 0,0 \纠正\)，能量特征值为\ (V_{0} = - \压裂{\三角洲}{2}\)．

在这里，通过米尔本方程探讨了量子-谐振腔相互作用的时间演化和退相干对量子-谐振腔动力学的内在影响29，

$ ${对齐}\ \开始压裂{d{\ρ}}{\帽子(t)} {d t} & = -我[{\帽子{H}},{{\ρ}}\帽子(t)) - \压裂{\伽马}{2}({H}}{\帽子,[{\帽子{H}},{{\ρ}}\帽子(t)]], \{对齐}$ $
(6）

在哪里\γ(\ \)表示内在退相干，其中量子相干性随着系统演化而自然丧失。这种内在退相干过程被引入，作为对标准量子力学演化的一种修正，它建立在量子位谐振器系统动力学在足够短的时间步长的随机连续相同的幺正变换下而不是连续的幺正演化的假设之上29．在本征退相干模型中，密度矩阵的非对角线元素在能量本征态基中被本征抑制，从而实现本征退相干而不耗散。

为了找到微分米尔本方程的特解，我们假设初始量子比特状态处于激发态\(|1\rangle \langle 1|\)．而初始谐振腔态是两个“相反”相干态的叠加态\(|\pm \alpha \rangle\)(这两个叠加态是\π(\ \)相移)，初始谐振腔的约简密度矩阵为

$ $ \{对齐的开始 } \!\!\!\!\!\!{\帽子{\ρ}}_ {R}(0) & = \压裂{1}{一}(α| \ \捕杀+ R | -α\ \捕杀)(α| \ \捕杀+ R | -α\ \捕杀)^{\匕首}\{对齐}$ $
(7）
$ ${对齐}& = \ \开始和_ {m, n = 0} P_ P {m} ^ {*} _ {n} | m \纠正\ langle n |, \{对齐}$ $
（8）

一个设计归一化因子，并给出光子分布函数

$ $ \{对齐}开始P_ {n} = \压裂{[1 + r (1) ^ {n}] \α^ ^ {n} e{- \压裂{1}{2}| \α| ^{2}}}{\√6 {(1 + r ^{2} +α2 r \ langle \ | -α\ \纠正)n !}}。\{对齐}$ $
（9)

的值\(r= 0,1， -1\)分别对应一个相干态、一个偶相干态和一个奇相干态。

要求解Eq. (6的哈密顿量的初始态和能量本征值重新表示。(2)，满足特征值问题的条件:\({\帽子{H}} | S_ {k} ^ {n} \捕杀= V ^ {n} _ {k} | S_ {k} ^ {n} \纠正(k = 1, 2) \)，\ (V ^ {n} _ {k} \)对应于特征值。因此，使用Eq. (6)，被修饰态的密度矩阵动力学，\ (^ {mn} _ {kl} (t) = | S_ {k} ^ {m} \纠正\ langle S_ {k} ^ {n} | \)，它们的表达式如下

$ $ \{对齐}年代开始^ {mn} _ {kl} D (t) & = ^ {mn} (t) e ^ {- i \λ(V ^ {m} _{我}- V ^ {n} _ {j}) t} | S_ {k} ^ {m} \纠正\ langle S_ {l} ^ {n} |, \{对齐}$ $
（10）

在哪里\ (^ {mn} (t) = e ^{- \压裂{\伽马}{2}(V ^ {m} _ {k} - V ^ {n} _ {l}) ^ {2} t} \)表示本征退相干项。然后，利用初始状态和哈密顿量(2)，则Eq. (6)则

$ $ \开始{对齐}{{\ρ}}\帽子(t) & = \总和_ {m, n = 0} P_ P {m} ^ {*} _ {n} \[罪罪\ζ_ {m} \ \ζ_ {n} H ^ {mn} _ {11} S ^ {mn} _ {11} (t) + \罪\ζ_ {m} \因为\ζ_ {n} H ^ {mn} _ {12} S ^ {mn} _ {12} (t) \ nonumber \ \ & + \因为罪\ζ_ {m} \ \ζ_ {n} H ^ {mn} _ {21} S ^ {mn} _ {21} (t) + \因为\ζ_ {m} \因为\ζ_ {n} H ^ {mn} _ {22} S ^ {mn} _ {22} (t)), \{对齐}$ $
（11）

在哪里\ (l = C \)对于初始相干态和\ (l = Ec \)对于初始偶相干态，缩写为:

$ $ \{对齐}开始H ^ {mn} _ {kl} = e ^ {- i (V ^ {m} _ {k} - V ^ {n} _ {l}) t - \压裂{\伽马}{2}(V ^ {m} _ {k} - V ^ {n} _ {l}) ^ {2} t}。\{对齐}$ $
（12）

光学层析成像的动力学研究主要建立在谐振腔约简密度矩阵上，

$ $ \{对齐的开始 } \!\!\!\!\!\!\!{\帽子{\ρ}}_ {}R (t) = \ ! \ \ ! !\总和_ {m, n = 0} P_ P {m} ^ {*} _ {n}(\气_ {1}| m \纠正\ langle n | + \气_ {2}| m + 2 \纠正\ langle n + 2 |), \{对齐}$ $
（13）

与

$ ${对齐}\ \开始气_{1}& = \罪^{2}\ζ_ {m} \罪^{2}\ζ_ {n} H ^ {mn} _{11} + \罪^{2}\ζ_ {m} \因为^{2}\ζ_ {n} H ^ {mn} _{12} \ \ & \四+ \因为^{2}\ζ_ {m} \罪^{2}\ζ_ {n} H ^ {mn} _ {2 l} + \因为^{2}\ζ_ {m} \因为^{2}\ζ_ {n} H ^ {mn} _{22}, \ \ \气_{2}& =罪\罪\ζ_ {m} \ \ζ_ {n} \因为\ζ_ {m} \因为\ζ_ {n} (H ^ {mn} _ {11} - H ^ {mn} _ {12} - H ^ {mn} _ {21} + H ^ {mn} _{22})。\{对齐}$ $

所产生的场态的光学层析成像动态将在下一节中基于简化的腔密度矩阵进行探讨{\ \({\帽子ρ}}^ {f} (t) \)．

图1
图1

相干态的光学层析成像轮廓如图(一个)的偶相干态(b)，而(c)\(| \α| ^ {2}= 9 \)．在(d)，在相干态和偶相干态的子图中，绘制了相干态在退相干和失谐作用下的谐振腔场熵的动态。

全尺寸图像

光学层析分布

利用谐振腔约简密度矩阵计算腔态随时间变化的光学层析成像{\ \({\帽子ρ}}_ {R} (t) \)作为46：

$ $ \开始{对齐}T(\λ_{\θ}\θ= \ langle{\帽子{\λ}}_{\θ}|{\帽子{\ρ}}|{\帽子{\λ}}_{\θ}\纠正\{对齐}$ $
(14）

在哪里\(|{\hat{\Lambda}}_{\theta}\rangle\)设计零差正交算子的特征态

$ $ \开始{对齐}{\帽子{\λ}}_{\θ}= \压裂{1}{\ sqrt{2}}({\帽子{\ psi}} \ exp - i \θ+{\帽子{\ psi}} ^{\匕首}\ exp我\θ),\{对齐}$ $
(15）

与特征值\(\Lambda _{\theta}\)和本振相\θ(\ \)．{\ \({\帽子psi}} \)而且\({\hat{\psi}}^{\dagger}\)是单模场操作符。方程(14)验证归一化关系

$$\begin{aligned} \int T(\Lambda _{\theta}，\theta)d\Lambda _{\theta}=1。\{对齐}$ $
（16）

在写出单模腔场密度矩阵后{\ \({\帽子ρ}}_ {R} (t) \)式的(13)的数字状态表示形式为:{\ \({\帽子ρ}}_ {R} (t) = \ \和限制_ {m, n = 0} ^ {\ infty} \ρ^ {mn} _ {R} | m \纠正\ langle n | \)时，我们将此表示形式代入(14)．因此，光学层析成像的表达式为

$ $ \开始{对齐}T(\λ_{\θ}\θ,T) & = \ \和限制_ {m, n = 0} ^ {\ infty} \ρ^ {mn} _ {R} (T) Z_ {m}(\λ_{\θ}\θ)Z_ {n} ^{*}(\λ_{\θ}\θ),\{对齐}$ $
(17)

与

$ $ \{对齐}开始Z_ {m}(\λ_{\θ}\θ= \ langle \λ_{}\θ,θ\ | m \捕杀= \压裂{e ^{- \压裂{间{\θ}^{2}}{2}}}{\π^{\压裂{1}{4}}}\压裂{e ^ {im \θ}H_ {m}(\λ_{\θ})}{\√6 {m ! 2 ^ {m}}}。\{对齐}$ $

在哪里\ (H_ {n} (.) \)指示顺序n埃尔米特多项式。方程(17)描述了系统中光学层析成像的时间动态，包括由Eq. (2)．在接下来的章节中，我们将研究在存在本征退相干的情况下，各种初始相干态的光学层析成像的时间演化。

图2
图2

动力学的光学层析成像轮廓的初始相干态\(| \α| ^ {2}= 9 \)用不同的时间表示\(\lambda t= \frac{1}{4}\pi\)在(一个)，\(\lambda t= \frac{1}{2}\pi\)在(b),\ (t = \π\ \λ)在(c)．在(d)、(c)在失谐效应下\(δλ= 10 \ \ \)是绘制。

全尺寸图像

光学层析动力学

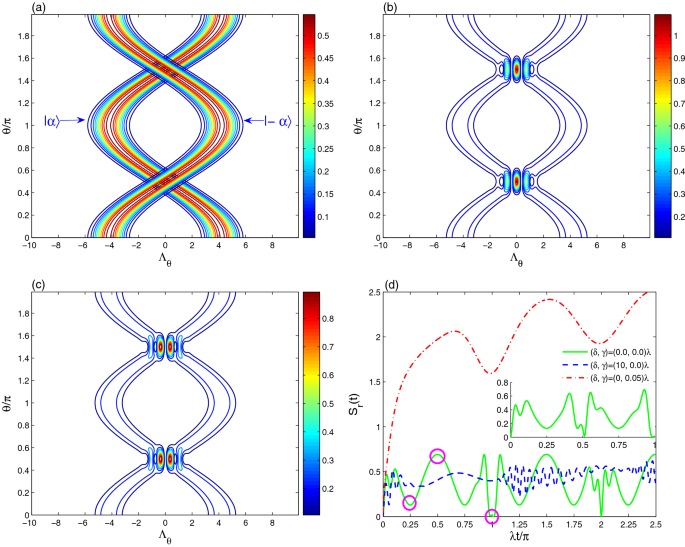
在无花果。1，为光学层析成像轮廓\(T(\Lambda _{\theta}， \theta, T =0)\)分别对相干态(CSs)、偶相干态(ECS)和奇相干态(OCS)进行了说明。数字1A表示两个“相反”相干态的光学层析成像\(|\pm \alpha \rangle\)．光学cs层析成像\(α| \ \捕杀\)行为类似于正弦曲线函数π\ [2 \ \)-周期和恒定的振幅\(\theta -\Lambda _{\theta}\)飞机。在这种情况下，对于本振相位角的增加(\(\theta \右tarrow 2\pi\))，光学cs断层扫描从该点开始\((\λ_{\θ}\θ)= (alpha | | \ \ sqrt {2}, 0) \ simeq (4.2426, 0) \)增加到这一点\((-4.2426， \pi)\)，然后向该点递减\((4.2426, 2\pi)\)．而光学cs层析成像\(| -α\ \纠正\)表现为余弦曲线函数。光学断层扫描\(|\pm \alpha \rangle\)有两个相反的分布依赖于相干强度\ (alpha | | \ \)．

数字1b说明光学ecs层析成像轮廓以相交的规则余弦曲线路径表示。ecs层析成像也描述了两个“相反”相干态的叠加\(|\pm \alpha \rangle\)．插入- colobar表明，层析成像分布具有恒定的振幅\(\Lambda _{\theta}-\theta\)-平面，干扰区域除外。振幅的分布是不同的，当ecs层析成像趋向中心点时，振幅增强\((\θ,\λ_{\θ})=(\压裂{1}{2}(2 n + 1), 0) (n = 0,1) \)．图的结果。1b,c表明ECS和OCS的光学层析成像仅在干涉区域存在差异。这种差异取决于初始相干场强度。证明了在大场强下，偶相干态和奇相干态的非经典性质近似相同9，47．因此，我们的研究主要集中在相干态和偶相干态。

为了研究光学层析成像与谐振腔量子相干动力学之间的关系，谐振腔场熵在退相干和失谐效应下的时间演化如图所示。1d.谐振腔熵计算公式为:

$ $ \{对齐}开始S_ {r} (t) = - \总和_ {n} \π^{我}_ {n} \ \ \ ln \π^{我}_ {n} \{对齐}$ $
（18)

在哪里\ \(π^{我}_ {n} \)表示谐振腔降密度矩阵的特征值{\ \({\帽子ρ}}_ {R} (t) \)式的(13)．图的实体曲线。1D表示量子位-谐振腔相互作用湮灭了谐振腔场的相干性(即，谐振腔产生的混合性增加)。图的子图。1D说明了偶相干态在第一阶段的振荡行为\π(\ \)期。注意在\(\lambda t= \frac{1}{2}\pi\)，如果谐振腔的初始状态是相干态，则谐振腔可以处于混合态;如果谐振腔的初始状态是偶相干态，则谐振腔可以处于纯态。在考虑量子位谐振子失谐效应后，产生谐振子混合的规律性消失了。振荡越多，混合性就越强。图中的点和虚线点曲线。1D表明谐振子熵由于内在退相干而增加，换句话说，产生的谐振子混合增强。

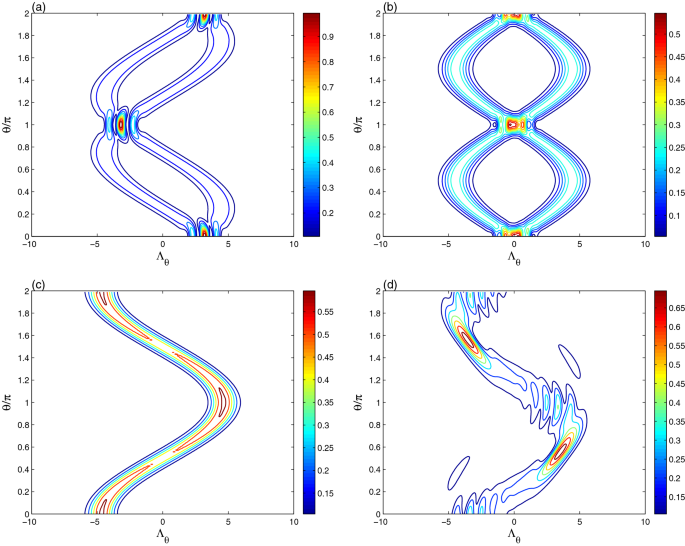
数字2说明了相干态光学层析成像的动力学过程\(α| \ \捕杀\)在共振情况下的量子位-谐振子相互作用\δ= 0 (\ \)．在\ (t = \压裂{1}{4}\π\)(谐振腔态具有部分相干)，光学cs层析成像演化为围绕轴的两个对称分布分支\(π\θ= \ \)，见图。2a.干扰区域的最大值大于图中初始分布的最大值。1一个。\ (t = \压裂{1}{2}\π\)时，生成的光学cs层析成像具有两条不规则的正弦路径，其形状类似于均匀相干态的初始分布。光学层析成像演化可作为量子比特-谐振腔相互作用产生的场谐振腔混合的良好指标。

所显示的光学cs层析成像证实了这一结果\(\lambda t =\pi\)(谐振腔状态为纯态，如图所示。1d).生成的谐振腔状态呈现出与相干态相似的余弦曲线函数的光学层析成像\(| -α\ \纠正\)，见图。1a.这意味着产生的纯谐振子态是相干态\(| -α\ \纠正\)．

数字2D表示相干态光学层析成像的相关性\(α| \ \捕杀\)，生成于\(\lambda t =\pi\)，与失谐\(δλ= 10 \ \ \)．由于量子谐振腔失谐的增加，光学层析成像的振幅和强度都得到了增强。

图3
图3

说明了本征退相干对图的光学层析动力学的影响。2b, c为\(λ\γ= 0.05 \ \)．

全尺寸图像

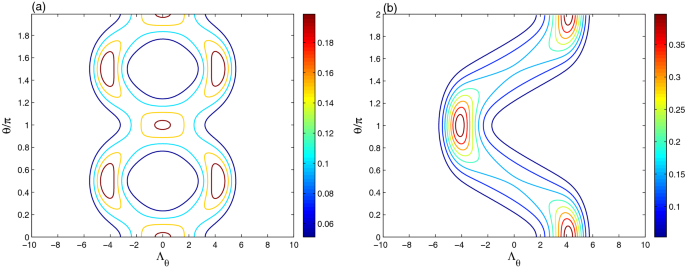
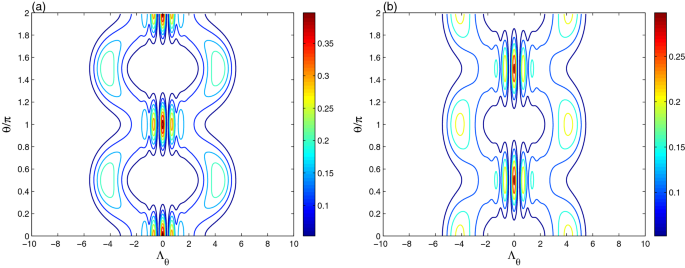
数字3.，表现出本征退相干效应\(λ\γ= 0.05 \ \)在不同时间生成的光学cs断层扫描上\(\lambda t= \frac{1}{2}\pi\)而且\ (t = \π\ \λ)无花果。2b, c。本征退相干效应导致:(1)cs光学层析成像的振幅和轮廓强度在不同时间都有所降低。在\(\lambda t= \frac{1}{2}\pi\)而且\ (t = \π\ \λ)时，由于本征退相干效应，分布形状大小发生变化。

在共振的情况下，我们观察到光学层析成像的周期性规则动态，可以被认为是场谐振器状态纯度的一个指标。生成的光学层析成像的规律性随着量子比特-谐振子失谐的增加而消失，即由于量子比特-谐振子相互作用而产生另一种纯相干谐振子状态的概率非常低。本征退相干增加了产生的场谐振腔状态的混合，导致干涉光学层析成像区域消失。

图4
图4

动力学的光学层析成像轮廓的初始均匀相干态为\(| \α| ^ {2}= 9 \)用不同的时间绘制\(\lambda t= \frac{1}{4}\pi\)在(一个)，\(\lambda t= \frac{1}{2}\pi\)在(b),\ (t = \π\ \λ)在(c)．在(d)、(c)在失谐效应下显示\(δλ= 10 \ \ \)．

全尺寸图像

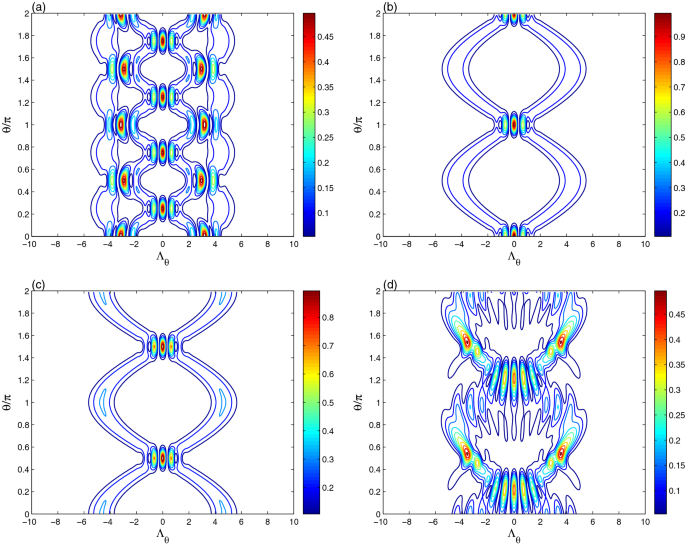
在无花果中。4，对于量子比特-谐振腔相互作用，初始均匀相干态在不同时间的光学层析成像轮廓的动力学\(\lambda t= \frac{1}{4}\pi\)，\(\lambda t= \frac{1}{2}\pi\)而且\ (t = \π\ \λ)是绘制。对于共振情况\δ= 0 (\ \)而且\(\lambda t= \frac{1}{4}\pi\)等高线图表明，光学层析成像具有更多的锯齿(出现在高强度)和更多的交叉对称和规则路径。生成的光学ecs层析成像的振幅和轮廓强度均小于初始均匀相干态的振幅和轮廓强度，如图所示。1b。\(\lambda t= \frac{1}{2}\pi\)(见图。4b)，谐振腔简化矩阵为具有两条规则正弦曲线路径的光学ecs层析成像提供了一种新的形状。它类似于图的初始偶相干态。1b是由谐振子熵的动力学所期望的，见图的子图。1d.为了证明光学ecs层析成像与谐振腔场熵之间的关系，显示了当时的ecs层析成像\ (t = \π\ \λ)(\ (S_} {R (t) = 0 \))．值得注意的是，生成的ecs断层扫描可以大致恢复到初始分布。

图5
图5

本征退相干对图的光学层析动力学的影响。2b, c为\(λ\γ= 0.05 \ \)．

全尺寸图像

数字4d证实了量子位谐振器失谐改变了光学ecs层析成像的振幅、频率和形状。

数字5显示了相干态在不同时间对层析动力学的本征退相干效应\(\lambda t= \frac{1}{2}\pi\)而且\ (t = \π\ \λ)(无花果。4b, c)。由于本征退相干效应，ecs层析振荡的振幅和强度减小，分布的形状改变。

从无花果。1而且2，我们注意到的振幅，频率和形状的光学层析成像\(α| \ \捕杀\)是时间。因此，量子位-谐振器相互作用允许制备特别不同的有趣的状态。用相干态作为初始态不能对光学层析成像进行保护。生成的ecs层析成像可以恢复到偶/奇相干态的初始分布，如图所示。1而且4．因此，我们推断出光学层析保护信息依赖于初始相干/偶相干谐振腔状态。

结论

我们探索了由一个量子比特和一个由双光子相互作用耦合的谐振器形成的量子系统的动力学。我们分析了谐振腔态的光学层析成像和量子相干动力学，当谐振腔态最初处于相干态的叠加状态时，存在内禀退相干。结果表明，由于量子-谐振腔相互作用，光学层析成像与产生的谐振腔量子相干性之间存在联系。我们研究了量子比特谐振腔失谐和本征退相干对初始相干和甚至相干谐振腔态光学层析分布动力学的影响。当量子位谐振腔失谐和本征退相干增强时，振幅和强度以及光学层析成像结构发生了显著变化。