随机微分方程的稀疏推理与主动学习

在整个自然科学中，数学模型经常被表述为微分方程。例如，随机方程、常微分方程和偏微分方程(SDEs、ode和PDEs)。在物理学中，控制微分方程通常来源于第一性原理，例如，能量和动量守恒，以及热力学方面的考虑。然而，对于所研究的复杂系统，例如在生物物理学、气候科学和神经科学中，决定系统特性的基本原理通常并不完全清楚。例如，因为这样的系统处于驱动的非平衡状态，高度非线性，并且因为动态可能发生在多个没有很好分离的尺度上。在这些情况下，人们可以求助于现象学的、有效的描述，这些描述可能源于某种程度的粗粒化，并基于实验数据。最近，计算能力的提高使得以自动化的方式构建这样的模型成为可能，这被称为控制方程的数据驱动发现。

已经发展了各种方法来直接从测量数据推断控制非线性动力系统的微分方程^{1，2，3.，4，5，6}．在一种被称为“符号回归”的流行方法中，函数库被用于根据某些优化准则自动提取控制方程中最能代表测量数据的项^1，2．最近，使用稀疏回归技术进行符号回归已经得到了相当大的科学关注^3.，4．在符号回归中，物理量z为说明起见，这里取它为标量，假设它服从一般形式的方程

在哪里\({\检查{z}} \)可以是，例如，时间导数\({\check{z}}=\frac{\partial z}{\partial t}\)用于描述ODE。\ ({\ mathcal {F}} (z, \ {\ textbf {x}}, \, t \, c) \)未知函数的参数是什么\ ({\ textbf {x}} \)表示空间坐标，而t表示时间和c是一个常量参数。向量和数组用粗体字母表示。符号回归的目的是估计函数\ ({\ mathcal {F}} (\ ldots) \)从一个数据集\ ({\ textbf {z}} \)的测量值序列z在不同的时空坐标下。向量\ \检查{\ textbf {z}} \)是从哪里测量或估计的\ (\ textbf {z} \)例如，用离散差分格式。的推论\ ({\ mathcal {F}} (\ cdots) \)，即所谓的“图书馆”矩阵\ ({\ varvec{\θ}}({\ varvec {z}}) \)是由一个合适的函数集构造的\ ({\ textbf {z}} \)的各种幂\ ({\ textbf {z}} \)，偏导数的组合，或三角函数。假设控制方程为(1)可以表示为库术语的线性叠加，我们写道

在哪里\ ({\ varvec {\ xi}} \)是一个权向量。控制方程的推理因此被简化为最优的回归问题\ ({\ varvec {\ xi}} \),鉴于{\ \({\检查textbf {z}}} \)而且\ ({\ varvec{\θ}}({\ varvec {z}}) \)．一般来说，求解Eq. (2)不是直接的，因为矩阵\ ({\ varvec{\θ}}\)应该表示许多方程项，可以有一个大的条件数\(\kappa ({\varvec{\Theta}})\)．

在裁判。^3.，提出了一种非线性动力学稀疏辨识(SINDy)方法。该方法可以迭代地工作。在每次迭代中，\ ({\ varvec {\ xi}} \)首先从涉及Eq. (2),\ ({\ varvec {\ xi}} \)随后的阈值是否小于截止值\ \ varkappa \ ()都设为0。迭代继续进行，直到满足收敛条件为止。SINDy已被证明是一种强大且通用的方法，适用于各种类型ode的推断^3.．但是，该方法需要用户手动选择阈值\ \ varkappa \ ()．对于偏微分方程的识别，一种称为列车顺序阈值岭回归(TrainSTRidge)的替代算法已在参考中描述。⁴．该方法是用于岭回归的最小二乘优化程序的变体，称为顺序阈值岭回归(STRidge)。在STRidge中，向量\ ({\ varvec {\ xi}} \)首先使用脊回归计算固定正则化参数。然后，把所有元素都放进去\ ({\ varvec {\ xi}} \)它们的绝对值小于阈值\ \ varkappa \ ()都设为0。都是正则化参数和阈值\ \ varkappa \ ()需要用户在STRidge中提供。TrainSTRidge⁴采用L0正则化和训练步骤自动确定阈值\ \ varkappa \ ()而正则化参数则由专业用户设置。相反，一种称为阈值稀疏贝叶斯回归的方法，也被用于识别偏微分方程⁷，不需要输入正则化参数，但一些阈值仍然由用户提供。

这项工作的第一个目标是提供一种方法来解决与控制物理方程的数据驱动发现相关的逆问题，Eq. (2)，通过结合贝叶斯方法和自动阈值过程。我们称这个方法为自动阈值稀疏贝叶斯学习(ATSBL)。我们的算法不需要任何手动微调参数来正确地从测量数据推断控制微分方程。该方法可用于ode、pde和sde的识别。

sde的情况需要特别注意，因为上述的方程推理方法主要是针对确定性过程和一些适量的加性噪声设计的。如何重建随机过程的力场的问题已经在许多研究中进行了研究，例如在软物质物理学和生物物理学中的应用^{5，8，9，10，11，12，13}．近年来，人们提出了一些复杂的方法来处理二阶动力学系统的离散化和推理问题^{14，15，16，17}．在这里，我们着重于使用符号回归来推导过阻尼朗之万型sde的解析表达式。在这种情况下，符号回归的一种方法是将相空间划分为小的超立方体，在一维情况下也称为箱。在每个超立方体中估计状态变量及其导数的平均值，并根据这些平均值定义回归⁵．这种平均通常取决于所选择的离散化，平均可能会导致大量的信息损失。此外，将这种方法应用于非平稳过程需要大量的轨迹集合和相当大的数值工作来采样相空间中与时间相关的概率分布。在相空间中求平均的困难激发了以下问题的研究:在不需要执行特别平均的情况下，上述推断工具可以在多大程度上用于有噪声的数据，以及最终如何在这种情况下提高推断方法的鲁棒性。我们表明，在推断的模型上施加拉普拉斯或高斯先验分布通常足以直接从轨迹识别正确的sde，而不需要相空间分仓，并且我们提供了两种先验分布获得的结果的准确性的比较。一个显着的性能，拉普拉斯先验证明了几个例子，包括布朗运动在时间相关势。

SDEs推理的一个主要挑战是，在可用数据中，相空间的采样通常非常不均匀。例如，当系统的长期动态由不同的局部稳定状态之间的过渡所主导，而短期动态则由个体稳定状态周围的波动所主导时，就会遇到这个问题。在这种情况下，推断的方程可能只在局部有意义，即在测量轨迹覆盖的区域内，并且从给定的数据集推断全局动态可能是先验的不可能。为了能够在这些条件下对全局模型进行自动推断，我们考虑了如何对系统设计外部扰动的问题，也称为“控制力”，这样状态变量就被迫在较短的采样时间内探索完整的相空间。为此目的而建立的伞形抽样例程依赖于二次控制力，并涉及控制力的非平凡设计步骤^{18，19，20.，21}．参见参考文献。^22，23用于替代方法。这种方法已被证明是有用的，例如，在成核的计算研究的背景下²⁴和经济增长²⁵流程。我们开发了一种可选的自适应控制技术，该技术递归地推断控制方程，并仅根据推断方程自适应外部控制。自适应循环由控制方程的推断和随后的控制力的更新组成，使其与推断的力直接相反。采用该自适应方案设计控制不需要调整参数。使用自适应控制方案，我们证明了一个实质性的改进，推理的SDEs的几个不同的模拟布朗运动。

工作安排如下:“方法一节详细介绍了函数库的构造和将推理问题转换为线性方程组的方法。总结了推理算法，并解释了如何使用拉普拉斯先验分布对推断模型施加稀疏条件。在“结果节中，通过数值算例说明了所述方法的性能，并与先前所述方法进行了比较。提出了一种改进SDEs推理的自适应采样技术，并证明了该方法的有效性。

常微分方程和偏微分方程

来自感兴趣的系统的测量数据假定被记录为状态的时间序列，例如，与时间相关的位置向量。在一个数据驱动的方法来建模一个系统，数据被用来自动推断一个先验未知的动态方程，控制观察过程。在这项工作中，推理是基于控制方程的候选函数库。用于微分方程推断的数据假定包含加性噪声，但没有系统误差。

对于ode的推断，我们推广了标量变量z, Eq. (1)，到一个系统米假定以相同的规则时间间隔对所有组件进行采样的组件\(\ell \in \{1\ldots M\}\)组件。为了区分离散测量和连续变量，下面采用下标表示法。的\ \)(\拼在有序时间序列中测量的第一个分量\ ([t_{1},识别\点,t_ {N}]识别\)写为\ ({\ textbf {z}} _{\魔法}= [z_ {\ l形,t_{1}}识别,\;z_ {\ l形,t_{2}}识别,\;\点\;z_ {\ l形,t_ {N}}识别]\)．包含多个变量测量值的向量或数组，例如，在不同的时间点，用粗体字母表示。整个数据可以写成矩阵形式

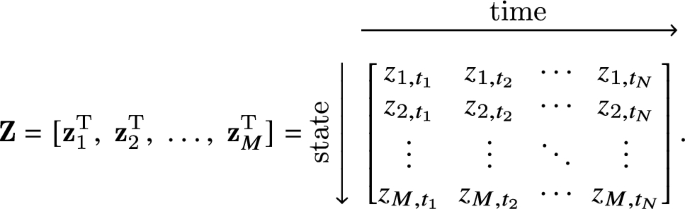
我们的方法还需要测量数据的导数。为了简单起见，在整个工作中使用有限差分近似。近似导数由算子表示\ ({\ mathcal {D}} _ {\ ldots} \)，这里表示四阶有限中心差分格式。例如，一个时间导数\ \)(\拼-th状态分量，\ ({\ textbf {z}} _{\魔法}\)，在我th的计算\ (t_{我}\识别)写为\({\点{z} _{\魔法}(t)} | _ {t = t_{我}识别}\大约{\ mathcal {D}} _ {t} {\ textbf {z}} _{\魔法}| _ {t = t_{我}识别}\)．对于整个数据集，我们将时间导数写成

包含轨道的矢量的控制ODE\ \)(\拼-状态分量可以写成所有初等函数的线性组合\ (\ {{\ textbf {z}} _ {\ l形的'}\}\)例如

这些指标\(\字母l ' \)，\ (\ \ l形”),\(‘\ \ l形”)覆盖了米系统维度,\ \ odot \ ()表示元素乘积，和c表示一个常数。\ ({\ mathcal {F}} _{\魔法}\)也可以依赖于时间，但接下来我们主要关注自主微分方程。自\({\mathcal{F}}_{\ell}(\cdot)\)表示可以从数据计算出的函数的线性组合，\({\mathcal{F}}_{\ell}(\cdot)\)可以用库矩阵来表示吗\ ({\ varvec{\θ}}({\ textbf {Z}}) \)与稀疏向量相乘\({\varvec{\xi}}_{\ell}\)．因此，对于Eq. (3.)离散化的形式

库矩阵的项在哪里\ ({\ varvec{\θ}}({\ textbf {Z}}) \)从测量数据中通过评估函数来计算\ (\ {{\ textbf {z}} _ {\ l形的'}\}\)的非零元素\({\varvec{\xi}}_{\ell}\)描述系统的动态特性。由于式(4)为ode，方程右侧的库中不含导数项。鉴于\ ({\ mathcal {D}} _ {t} {{\ textbf {z}}} _{\魔法}\)而且\ ({\ varvec{\θ}}({\ textbf {z}}) \)，目的是计算一个稀疏向量\({\varvec{\xi}}_{\ell}\)用最小数量的非零系数对应于描述动力学所必需的最小数量的项。

对于偏微分方程的推断，使用库矩阵\ ({\ varvec{\θ}}\)必须包含偏导项。因此，需要数据来允许对两个或多个变量(例如，关于时间和空间)的导数表达式进行数值估计。因此，测量通常由系统变量的离散时空序列记录组成。例如，一个数组\ ({\ textbf {Z}} ^ {P} \)代表米-维状态向量，在N时间点R一个空间坐标的位置x写为

通过有限差分近似，每个分量的时间导数矢量，\ ({\ mathcal {D}} _ {t} {\ textbf {z}} _{\魔法}\)，以及各种订单x导数的计算，例如，\ ({\ mathcal {D}} _ {x} {\ textbf {Z}} ^ {P} \; {\ mathcal {D}} _ {xx} {\ textbf {Z}} ^ {P} \; \ \点)．这些衍生项被添加到库中\ ({\ varvec{\θ}}^ {P} \)．类似于ode，控制组件的动力方程的推断\ ({\ textbf {z}} _{\魔法}\)是基于线性方程的吗

用一个稀疏系数向量\({\varvec{\xi}}_{\ell}\)待定。

请注意，在这个框架中，从噪声数据中对导数进行稳健估计是奥德斯和偏微分方程的数据驱动推理的重要前提。本文采用的四阶有限差分近似可以用其他方法补充或取代，包括去噪方法和高斯过程回归模型。

随机微分方程

我们专注于朗之文型sde来描述连续实状态变量的时间演化\ ({\ textbf {X}} (t) \)，表示布朗粒子在空间中的位置²⁶．轨迹，用\ ({\ textbf {X}} (t) \)，为空间坐标值的时序序列\ ({\ textbf {x}} \)．所考虑的sde的一般形式为

我们使用爱因斯坦和约定和\(间{\魔法}(t) \)表示\ \)(\拼-当时系统状态的第th个组成部分t．的轨迹\ ({\ textbf {X}} \)是利用伊藤对随机积分的解释来计算的²⁶．的\ (g_{\魔法}({\ textbf {X}} (t), t) \)表示微分方程的确定性部分。例如，对于一个布朗粒子，在具有势的保守力的存在下进行过阻尼运动\ (U ({\ textbf {x}}, t) \)，我们有\ (g_{\魔法}({\ textbf {X}}, t) = - \微分算符_{间{\魔法}}U ({\ textbf {X}}, t) | _ {{\ textbf {X}} = {\ textbf {X}} (t)} \)．假设随机扰动是由带有噪声源的维纳过程引起的\(\Gamma _{\ell}(t)\)而且\ ({\ textrm {d}} W_{\魔法}= \伽马_{\魔法}(t) \ {\ textrm {d}} t \)．假设噪声服从高斯分布，且均值为零\三角洲(\ \)-相关方差为

分别。系数矩阵\(h_{\ell，\ell '}\)式中(6)缩放随机扰动的大小，为简单起见，假定为对角线。进一步的噪声源，例如，从一个轨迹的实验测量，没有明确考虑整个工作。

对应Eq.的Fokker-Planck方程(6)，并描述了概率密度函数的演化\ (f ({\ textbf {x}}, t) \)是由

福克-普朗克算符在哪里\(\帽子{L} \)作用于\ (f ({\ textbf {x}}, t) \)有形式

的函数\ (D_{\魔法}^ {(1)}({\ textbf {x}}, t) \)而且\(D_{\ell，\ell '}^{(2)}({\textbf{x}}，t)\)被称为克雷默斯-穆瓦亚尔(KM)系数或漂移和扩散系数。在完全已知轨迹的前提下\ ({\ textbf {X}} (t) \)时，KM系数可由增量变化计算\(\三角洲间{\魔法}(t) \枚间{\魔法}(t + \τ)间的{}\拼(t) \)在无穷小的时间间隔内\ \(τ\)作为

在哪里\ (\ langle \ ldots \捕杀_ {{\ textbf {X}} (t) = {\ textbf {X}}} \)表示随机轨迹上的平均值。KM系数与函数有关\ (g_{\魔法}\)而且\(h_{\ell，\ell '}\)在朗之万方程中为

我们只考虑对角扩散矩阵，但KM系数可以显式地依赖于空间和时间。为了估计系数，米维轨迹\(间{\魔法,我}\)，\(\ell \in \{1，\dots,M\}\)用一个小的，规则的时间步长采样年代在时间点上\(i \in \{1，\dots,N\}\)．轨迹样品\(间{\魔法,我}\)与原始随机变量的区别\(间{\魔法}(t) \)按索引我，代表我-第th时间点。据此，构造两个新的序列为

在哪里年代是小时间步长吗⁵．的\ (\ varvec {F} _ \魔法^ {(1)}\)而且\ (\ varvec {F} _ \魔法^ {(2)}\)是由不可微的随机过程的样本轨迹构成的。利用这些量来估计KM系数，以式(10)使得有必要首先对随机过程进行广泛的采样，然后近似于平均值\ (\ langle \ ldots \捕杀_ {{\ textbf {X}} (t) = {\ textbf {X}}} \)在不同的实现过程。

请注意，基于Eq. (10)，我们忽略了在“现实世界”中测量的时间序列会出现的两个问题。首先，测量噪声可能使马尔科夫过程的假设在小尺度上无效²⁷．其次，有限采样间隔年代在实践中不能使其任意小，因此估计的KM系数系统地偏离真实系数^28，29．修正有限采样时间误差的方法可用于各种随机过程^{30.，31，32}．虽然本工作的重点是控制方程的推理问题，但在实际应用中应采用有限采样时间修正。

下面，我们采用两种不同的方法来估计漂移系数和扩散系数。首先，在下一小节中描述了一种方法，该方法基于相空间中数据的分箱来产生直方图。其次，我们将数据分箱的结果与KM系数的直接估计结果进行比较。

从分类数据估计KM系数

描述平稳马尔可夫时间序列的一种经典方法是基于空间间隔内轨迹数据的分组^5，33，34．对于这种方法，我们只关注一个空间维度的问题(\ (M = 1 \))．为了估计概率分布，随机过程的多个样本轨迹的数据被分组到问bin和每个bin中的值的平均值为

在哪里酒吧\ (\ {X} _ {k} \)，酒吧\ (\ {F} ^ {(2)} _ {k} \),酒吧\ (\ {F} ^ {(2)} _ {k} \)都是箱子平均数。估计的概率，找到轨迹部分在kth垃圾桶,\ (p_ {k} \)，归一化为\ \(和_ {k = 1} ^ {Q} p_ {k} = 1 \)与\(0\le p_{k}\le 1\)．由数据分箱直接产生的直方图产生了漂移和扩散系数的曲线，参见参考文献。^5，33．KM系数的方程，\ (^ {(1)} (x) \)而且\ (^ {(2)} (x) \)的解析表达式{\ \({\酒吧textbf {F}}} ^{(1、2)}\)作为函数{\ \({\酒吧textbf {X}}} \)．为了这个目的，一个图书馆\ ({\ varvec{\θ}}\在{\ mathbb {R}} ^{问\乘以K} \)是由已打包的数据构造的，在哪里问箱子的数量是多少K是库中的项数。例如,\ ({\ varvec{\θ}}({\酒吧{\ textbf {X}}}) = [{\ textbf{1}}, \;{\酒吧{{\ textbf {X}}}}, \;{\酒吧{\ textbf {X}}} {\ odot{\酒吧{\ textbf {X}}}}, \;{\酒吧{{\ textbf {X}}}} \ odot \酒吧{{\ textbf {X}}} \ odot{\酒吧{\ textbf {X}}}, \;酒吧\罪({\ {\ textbf {X}}}), \;] \ \点)在哪里\ \ odot \ ()再次表示元素乘积。如果库包含了分析描述KM系数所必需的所有函数表达式，则控制方程可以写成

在哪里\ ({\ textbf {W}} ^ {(1)} \)而且\ ({\ textbf {W}} ^ {(2)} \)为两个稀疏向量，其非零项对应于KM系数寻找解析表达式中所包含的库项。方程(14个)的收益率\ (^ {(1)} (x) \)和Eq. (14 b)的收益率\ (^ {(2)} (x) \)．求最优的逆问题\ ({\ textbf {W}} ^{(1、2)}\)式中(14)的形式与Eq. (2)．

轨迹的装箱可以在稀疏采样区域产生显著的误差，无论是在采样相空间的内部和边界。我们提出可以通过去除或过滤具有高不确定性的容器来改进sde的识别。为了证实这一建议，我们实现了对未经过滤的直方图的推断过程，此外，实现了一个直接的扩展，基本上包括固定一个小概率阈值，低于该阈值的所有数据都将被丢弃。虽然概率阈值可以通过不同的方式确定，但我们在这里使用了一种最初用于图像边缘检测的自动启发式方法³⁵．参考文献中描述的过程。³⁵包括根据概率阈值划分数据，分别最大化Shannon和Tsallis熵。最大化香农熵产生阈值，将数据分为“前景”和“背景”，分别对应于信号主导和噪声主导的相空间区域。确定“背景”的阈值然后在第二步中通过最大化Tsallis熵来改进，其伪可加性据称改善了包含远程相关性的数据的分析，参见参考文献。³⁶．虽然我们发现这种确定概率阈值的方法在实践中是有用的，但就我们所知，它的理论基础并不完全清楚。因此，在某些情况下，基于结果手工选择概率阈值可能更可取。

KM系数的无数据分箱估计

估计KM系数的一个更直接的方法是基于轨迹的使用\ ({\ textbf {F}} ^{(1)} _{\魔法}\)而且\ ({\ textbf {F}} ^{(2)} _{\魔法}\)没有装箱或过滤。由于我们不打算研究瞬态初始动力学，我们主要采用随机过程产生的单个长轨迹作为输入数据。为了从时空轨迹推断KM系数，我们构造了一个库\ ({\ varvec{\θ}}\在{\ mathbb {R}} ^ {N \乘以K} \),在那里N轨迹的长度和K是库中的项数。例如,\ ({\ varvec{\θ}}(\ {{\ textbf {X}} _ {\ l形 '}\})=[{\ \ textbf {1}}, {\ textbf {X}} _ {1}, \; \ ldots {\ textbf {X}} _ {M} \; {\ textbf {X}} _ {1} \ odot {\ textbf {X}} _ {2}, \;\ \点;\sin (\mathbf {X_{1}})，\ldots]\),在那里\(\字母l ' \)涵盖了所有米随机过程的分量。注意，库的构造是这样的F \(^{1} _{\魔法,我}\)而且F \(^{2} _{\魔法,我}\)在我-th时间点仅依赖于涉及坐标的函数\(\{X_{\ell '，i}\}_{\ell '}\)在同一时间点。因此，漂移和扩散系数估计量的速度依赖关系或历史依赖关系被排除在外。在假定库中包含了描述漂移系数和扩散系数的所有必要项的情况下\ \)(\拼随机过程的第-分量可以用

在哪里\(\ell \in \{1 \ldots M\}\)这些向量\ ({\ textbf {W}} ^{(1、2)}_{\魔法}\)在与KM系数的解析描述所需的库中的项相对应的条目中，为非零。确定\ ({\ textbf {W}} ^{(1、2)}_{\魔法}\)又是一个逆优化问题。

基于自动阈值稀疏贝叶斯学习的推理问题求解

用于识别相关的标准库术语，例如公式(15，我们提出了一种自动阈值稀疏贝叶斯学习(ATSBL)方法。该方法包括两个主要步骤。首先，用一种叫做贝叶斯压缩感知的拉普拉斯先验(BCSL)算法解决了反问题。³⁷．由于库很大，BCSL算法生成的解向量通常仍然包含相当多的不会消失但较小的条目。因此，在第二步中，通过自动阈值化过程去除对结果控制方程的可忽略不计的贡献^3.，5，7．下面将详细介绍该方法的这两个步骤。

基于拉普拉斯先验的贝叶斯压缩感知(BCSL)

我们考虑一个包含给定向量的一般线性方程组\ ({\ textbf {g}} \)和矩阵\ ({\ varvec{\φ}}\)和一个未知的稀疏向量\ ({\ textbf {w}} \)作为

其中向量\ ({\ textbf{年代}}\)表示噪声或测量误差。在这里,\ ({\ textbf {w}} \)可以认为是出现在方程迭代求解过程中的解向量。（5), (14)，或Eq. (15)．可以使用各种方法来计算稀疏解向量\ ({\ textbf {w}} \)由式(16)．特别是压缩感知的研究，它处理欠定系统的稀疏信号的重建，已经产生了广泛适用的，高效的方法来寻找稀疏解向量\ ({\ textbf {w}} \)．其中包括基于相关向量机(RVM)的贝叶斯方法。^38，39．如果用拉普拉斯分布作为先验概率分布，则得到非常稀疏的结果向量\ ({\ textbf {w}} \)．在这里，我们采用了一种称为贝叶斯压缩感知的方法，使用拉普拉斯先验(BCSL)³⁷．具体地说，我们使用BCSL的一个变体来交互地计算近似解，这是非常有效的计算，并为我们的应用类型产生准确的结果。

简单来说，BCSL的数学基础如下，见参考文献。³⁷．该方法基于一个三级层次模型。我们假设误差\ ({\ textbf{年代}}\)是从方差未知的零均值高斯分布中提取的\(1/\beta > 0\)．因此，求向量的似然函数\ ({\ textbf {g}} \)是由

未知向量\ ({\ textbf {w}} \)被分配了一个先验分布，它代表了我们对这个量的性质的认识。为了对稀疏性进行编码，人们会使用拉普拉斯先验\ (p ({\ textbf {w}} | \λ)= \λ/ 2 \ exp(λ- \ \ _{我}|总和w_{我}| / 2)\)使用超参数\λ(\ \)．然而，由于拉普拉斯先验不共轭于高斯似然，因此，使用这种拉普拉斯先验的积分计算并不容易实现。(17)．因此，一个非负超参数的辅助向量\ ({\ varvec{\伽马}}\)与\ ({\ textbf {w}} \)被用来表示先验为两个不同分布的卷积\ (p ({\ textbf {w}} | {\ varvec{\伽马}})=左\π_{我}\ [\ exp {(-w_{我}^{2}/(2 \伽马_{我}))}/ \√{2 \π\伽马_{我}}\右]\)而且\ (p ({\ varvec{\伽马}}| \λ)=左\π_{我}\[\λ\ exp{(λ- \ \伽马_{我}/ 2)}/ 2 \]\)．这两个分布加在一起就得到了一个拉普拉斯先验\ ({\ varvec{\伽马}}\)作为

看到裁判。⁴⁰．总的来说，联合概率密度结果为

其中参数\λ(\ \)而且β\ (\ \)都被假设服从伽玛分布。推断出最可能解向量的值\ ({\ textbf {w}} \)除了超参数外，还采用了后验概率的证据程序\ (p ({\ textbf {w}}, {\ varvec{\伽马}},\λ,β\ | {\ textbf {g}}) \)是最大的\ ({\ textbf {w}} \)，\ ({\ varvec{\伽马}}\)，\λ(\ \),β\ (\ \)，根据数据。通过使用这个表达

和Eq一起。19)，人们就会看到……的价值\ ({\ textbf {w}} \)后验的最大化可以通过简单的最大化来确定\ (p ({\ textbf {g}} | {\ textbf {w}}, \β)p ({\ textbf {w}} | {\ varvec{\伽马}})\)．该计算为结果向量生成表达式\ ({\ textbf {w}} ^{*} =β\ {\ varvec{\σ}}\ varvec{\φ^ {T}} {\ textbf {g}} \)与\ ({\ varvec{\σ}}=(β\ \ varvec{\φ^ {T} \φ}+ {\ varvec{\λ}})^ {1}\)而且\ (\ varvec{\λ}={诊断接头}\文本(1 / \伽马_{我})\)．的未知值，此步骤对应于Ridge回归\ ({\ varvec{\伽马}}\)，\λ(\ \),β\ (\ \)．通过最大化来确定这些超参数

关于\ ({\ varvec{\伽马}}\)，\λ(\ \),β\ (\ \)．在这里,\ (p ({\ varvec{\伽马}},\λ,β\ {\ textbf {g}}) \)由式的右边计算(19)通过积分出来\ ({\ textbf {w}} \)．使用BCSL的快速近似版本，确定超参数的最优值的方程是迭代求解的，其中只有向量的一个条目\ ({\ varvec{\伽马}}\)每一步都在调整。

自动阈值

逆问题的解(16)与BCSL通常产生向量\ ({\ textbf {w}} \)只包含一些大的条目，但也包含一些非常小的、非零的条目。去除这些可忽略的条目是可取的，我们用迭代阈值处理提高了解的稀疏性⁴．伪代码1说明了参考文献中提出的阈值处理方法。⁴与文献中提出的BCSL相结合。³⁷．简而言之，阈值算法的工作原理如下。输入由\ ({\ textbf {g}} \)，库矩阵\ ({\ varvec{\θ}}\)，初始增量\ (d_ {\ textrm {tol}} \)对于阈值托尔，最大迭代次数\ (n_文本{iter}} {\ \)．的数据\ ({\ textbf {g}} \)而且\ ({\ varvec{\θ}}\)分为培训和测试两部分。通常，80%的数据用于训练，20%用于测试。阈值是根据训练数据迭代计算的，阈值的有效性是根据其应用于测试数据所产生的误差进行评估的。该算法的核心部分是对稀疏向量进行迭代计算的循环\ ({\ textbf {w}} \)还有阈值托尔．在每个迭代步骤中，首先使用近似的快速BCSL例程来获得的估计\ ({\ textbf {w}} \)从训练数据中。通过计算计算结果与测试数据的误差来评估该方案估计的质量

其中解范数的惩罚因子选择取决于条件数为\(\eta =10^{-3}\，\kappa ({\varvec{\Theta}})\)，按照原算法的建议⁴．如果当前解的误差小于前几次迭代的误差，则接受新解并设置阈值托尔是增加了。反之，阈值减小，增量增大\ (d_ {\ textrm {tol}} \)是雅致。最终解决方案\ ({\ textbf {w}} _ {\ textrm{最好}}\)是稀疏向量，它决定了控制微分方程，sde, ode和pde中的项。

确定的控制方程的质量评分

在测试用例中，通过将结果与已知的原始微分方程集进行比较，可以直接量化推理程序的误差。为此，我们将识别系数(DIC)的偏差定义为

在每一个\ (w_{我}\)在已确定的方程中，系数是一项吗\ (w ' _{我}\)是用于生成测试数据的原始方程中的相关系数。这里，每对中至少有一个系数\ (\ {w_ {}, w ' _{我}\}\)要求非零，并且和只在这些系数上运行。K表示这些系数的个数。DIC位于该范围内\ ([0, \ infty] \)其中0表示完全恒等方程。

从噪声轨迹推断sde

我们首先用一维双阱位势中粒子过阻尼布朗运动的例子说明了数据驱动的sde识别x．该系统的漂移系数和扩散系数由

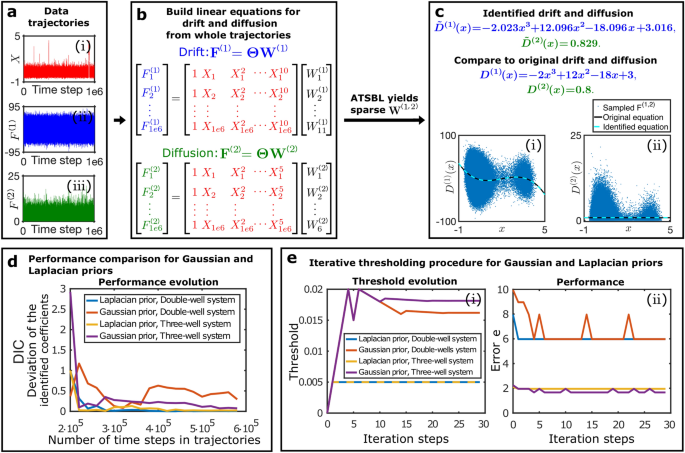
将Langevin方程与Euler-Maruyama方法进行积分，得到用于推导控制方程的轨迹数据。一个轨迹\ ({\ textbf {X}} \)如图所示。1ⅰ(\ (10 ^ {6} \)时间的步骤)。的轨迹\ ({\ textbf {F}} ^ {(1)} \)而且\ ({\ textbf {F}} ^ {(2)} \)如图所示。1a-ii,三世。为了可视化x-漂移系数估计量的依赖性，我们绘制\ ({\ textbf {F}} ^ {(1)} \)反对\ ({\ textbf {X}} \)，见图。1我。同样的,\ ({\ textbf {F}} ^ {(2)} \)是针对\ ({\ textbf {X}} \)作为扩散系数的估计量\ (^ {(2)} (x) \)在无花果。1c-ii。这两个图都在真实漂移和扩散系数周围表现出较大的波动，所得到的平均值显然容易出错，特别是在采样域的边界处。

利用弹道数据，我们接下来构建一个库，其中包括11项漂移系数和6项扩散系数，如图所示。1b.然后使用ATSBL进行识别\ ({\ textbf {W}} ^ {(1)} \)而且\ ({\ textbf {W}} ^ {(1)} \)直接从弹道出发，不需要装箱。所确定的x漂移系数和扩散系数的依赖函数如图所示。1我,二世。它们与用于创建数据的原始函数非常一致。带估计不确定性的识别方程如图所示。1c。

与已建立的推理技术相比，ATSBL的主要区别是对库系数先验的拉普拉斯分布的假设。更直接的，尽管理论上不太促进稀疏性的过程是使用高斯先验，对应于具有固定正则化参数的岭回归，用于解向量的推断\ ({\ textbf {w}} \)式中(16)，然后进行自动阈值划分，如参考。⁴．为了比较这两种方法对sde推断的性能，我们评估了识别系数DIC的偏差，作为用于推断的数据点数量的函数。结果如图所示。1d表示拉普拉斯先验优于高斯先验，因为它需要更少的数据，并导致更小的DIC。为了进一步建立ATSBL的鲁棒性，我们考虑了迭代阈值处理对两个先验分布的收敛性。结果如图所示。1e-i,ii证明了在拉普拉斯先验的情况下实现了更好的收敛。对于高斯先验分布和拉普拉斯先验分布，阈值和误差都在迭代过程中振荡，这是由于阈值分割过程中的自适应步长造成的。

带有时变漂移系数的sde推断

在前一节中，提供了一个例子，说明如何通过直接对轨迹数据进行回归来获得KM系数。直接使用轨迹数据对于处理时变力的更复杂情况变得尤为重要。在这种情况下，概率分布随时间而变化，基于直方图的动态分布近似在技术上具有挑战性，并且需要在相同的条件下获得许多样本轨迹。为了探究我们的方法在这种情况下的有效性，我们考虑一个粒子在一个随时间变化的一维势内扩散的例子。该系统的漂移系数和扩散系数由

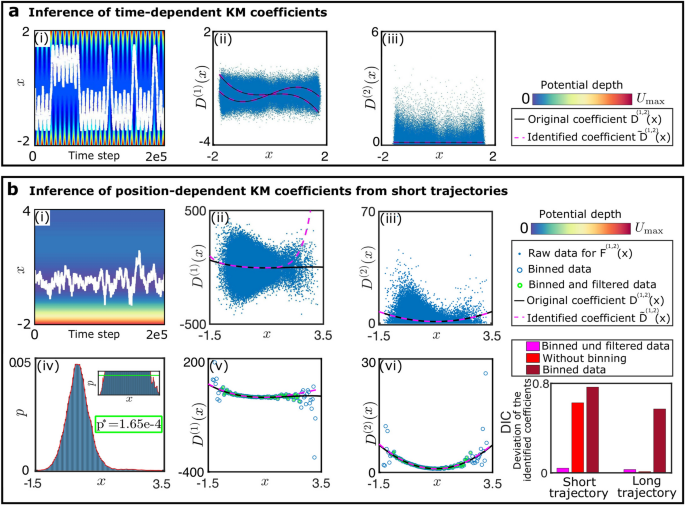
与\(a_{0}=5 \ * 10^{-3}\)．电势具有双阱形状，其中两个极小值的位置随时间变化。两个最小值从不同的位置开始，并定期合并为一个最小值，然后再次分离以达到初始位置。每当势阱彼此靠近时，跃迁概率就变大，粒子很可能从一个势阱转变到另一个势阱。这导致了两个潜在井之间的随机振荡。为了测试是否可以用从单一轨迹构建的库推断出基本方程，我们假设频率为ω\ (\ \)潜在的变化是已知的。从数据推断这个频率原则上也是可能的，但需要过多的计算能力，因为必须在库中考虑具有明确时间依赖性的高阶项。我们构造了一个由时间相关部分和时间无关部分组成的库。库的前半部分只是一个多项式基，后半部分对应于多项式基乘以a\(\cos (\ t)\)的因素。推理过程的结果如图所示。2a.推导的方程与正确的方程一致。为了说明，我们在图中绘制了原始方程和推断方程的漂移和扩散的快照。2a-ii,三世。请注意，即使仅使用一个样本轨迹进行推断，一阶sde的推断过程也显示出显著的性能。

用于从短轨迹推断sde的数据装箱

当在非均匀力场中遇到短轨迹时，依赖于直接使用样本轨迹进行回归的推断方法可能变得不可靠。在这种情况下，我们发现采用数据装箱更合适。我们用粒子在一维双阱势中的布朗运动来说明这个过程，其中扩散系数取决于空间。模型的漂移系数和扩散系数由

我们首先考虑有\ [2 \ * 10 ^ {5} \)时间步长，如图所示。2b我。原始数据和分箱数据如图所示。2分别是B-ii iii和b-v,vi。在本例中，使用了200个数据箱。由分箱数据近似得到的分布明显偏离已知函数\ (^ {(1)} (x) \)而且\ (^ {(2)} (x) \)在采样不足的地区。因此，对分箱数据进行过滤，去除不确定性较高的数据点。此筛选是按照“方法部分通过丢弃低于概率阈值的箱子\ (p ^ {*} \)这是由熵最大化决定的³⁵，见图。2b-iv。为了评估装箱和过滤是否也有利于从长轨迹推断sde，我们还使用了来自轨迹的数据\ [2 \ * 10 ^ {7} \)时间的步骤。数字2B-vii表示识别系数的误差。

对于短轨迹，结合滤波过程来抑制具有高不确定性的数据是有利的。产生这种结果的原因可以通过对图的检查来理解。2B-v,vi，其中推断的函数只在相空间中最密集的区域匹配正确的函数。因此，排除具有高度不确定性的数据点可以防止过拟合，并在轨迹不够长以允许对整个相空间进行充分采样的情况下改善基础动力学方程的推断。相反，无论是否滤波，数据装箱都不利于对整个相空间采样的长轨迹进行分析，如图所示。2b-vii。

主动采样提高了sde的识别能力

到目前为止，我们的注意力仅限于从分析之前产生的数据中提取估计，例如在实验中。因此，我们假设数据集的大小足够大，可以对控制方程进行某种形式的推断。在不同的场景中，人们可能有能力扰动所研究的系统，无论是在计算机模拟中还是在实验设置中，同时记录数据。然后，可以通过对系统施加适当设计的扰动来提高采样效率。一般来说，当系统表现出具有多个局部极小值的能量景观时，这种方法预计是有用的，这些极小值可以长时间捕获轨迹。我们描述了一种自适应控制方法，其中动态方程的推断与系统的同时扰动递归地导致相空间的全局探索，以提供充分的采样无处不在。

由于概率分布趋向于在局部能量最小值附近达到峰值，因此动力学方程可以在这些最小值附近进行局部估计。为了在迭代扩展采样区域的同时利用这种局部估计，我们重复地重新采样，同时在每个采样轮中应用与前几轮局部估计的系统力相反的控制力。这种方法直接应用的困难在于，控制力可以承认偏离初始估计区域的较大偏差。这种效应会产生很大的误差，减慢收敛速度，甚至可能导致发散问题。我们通过用高斯分布对控制力进行加权来克服这个问题，这样控制力就会从当前估计区域消失。这个局部控制力将轨迹从已经执行估计的能量最小值处排除，轨迹最终达到另一个局部最小值。

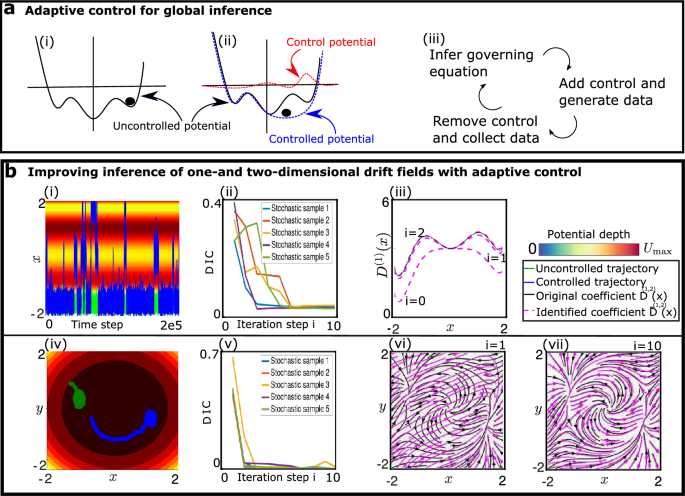
这种方法，我们称之为自动迭代采样优化(AISO)，如图所示。3.a, i-iii，伪代码在算法2中提供。在每一次迭代中，从之前所有迭代中积累的数据估计基础动力学方程。局部采用推断漂移项的负值作为控制力。控制力高斯权值的中心和宽度仅由前一步轨迹的均值和标准差计算。因此，我们定义作用于组件上的控制力\ \)(\拼作为

其中索引我指示将在迭代号处取值我；\(\mu _{\ell}^{i}\)而且\(\zeta _{\ell}^{i}\)表示从该步长提取的轨迹的均值和方差我在每次迭代中。经过足够次数的迭代后，将所有迭代积累的数据点进行组合，并从积累的数据中提取运动方程。对于预定义的迭代步骤数，重复此过程。对于下面给出的示例，迭代步骤号已固定为\ (N = 10 \)，因为在这些情况下，收敛在不到10步的时间内就实现了。

对于我们的方法的第一次演示，我们使用了三井电势\ (U (x) = x ^ {6} 6 x ^ {4} + 0.5 x ^ {3} + 8 x ^ {2} \)用常数扩散系数来模拟一维粒子的运动轨迹。漂移系数和扩散系数为

接下来，我们还考虑二维漂移场，由径向对称分量和剪切分量组成x，y飞机。漂移系数和扩散系数由

利用这些驱动力，我们用\ (10 ^ {5} \)时间步长为\(\ t=5\ * 10^{-3}\)．势图上的部分轨迹如图所示。3.我,第四。中间迭代步骤的结果和漂移场如图所示。3.b-iii, vi。随着算法迭代次数的增加，控制势的系数逐渐接近正确漂移场的系数，从每个局部最小值的剔除变得更加有效，如图。3.b-iii,七世。这导致粒子穿过鞍点的罕见事件增强，如图所示。3.B-i,iv通过受控和非受控轨迹。通过计算系数来量化误差波浪字符\ ({\ D {}} ^ {(1)} (x) \)而且波浪字符\ ({\ D {}} ^ {(2)} (x) \)在每次迭代中。迭代过程中DIC从1减小到接近0.01，如图所示。3.b-ii, v。因此，所确定的方程的项接近原始方程中给出的项。

常微分方程和偏微分方程的辨识

接下来表明，由ATSBL实现的基于拉普拉斯先验的稀疏推断方案也可以用于常微分方程和偏微分方程的数据驱动发现。从轨迹数据中识别ode被证明与洛伦兹系统，这是混沌行为的范例⁴¹．洛伦兹方程由

其中参数固定为= 10 \ \ ()，\ (b = 28 \),\ (c = 3/8 \)．我们对这些方程进行数值积分，得到如图所示的轨迹。4a.混沌系统包含两个吸引子。对于数据驱动的系统标识，我们使用三个相同的库\ ({\ varvec{\θ}}\)对于每一个变量，x，y而且z．\ ({\ varvec{\θ}}\)由模拟轨迹构建，包括56项，其中包含所有变量的最多四次幂。时间导数的计算采用四阶中心差分近似。由公式中所示的库构造的通用ode (4)由三个线性方程组表示。将推断程序应用于无噪声数据所得到的估计方程具有与时间步长的量级相当的小误差\(\ t = 2 \ * 10^{-4}\)，见图。4b.然后对加性高斯噪声的轨迹重复相同的推理过程。每个坐标上噪声的标准差选取为同一坐标上无噪声数据标准差的2%。在这种情况下，ATSBL识别的ode仍然包含所有正确的项，并且推断的系统参数的误差在百分比范围内，如图所示。4b。

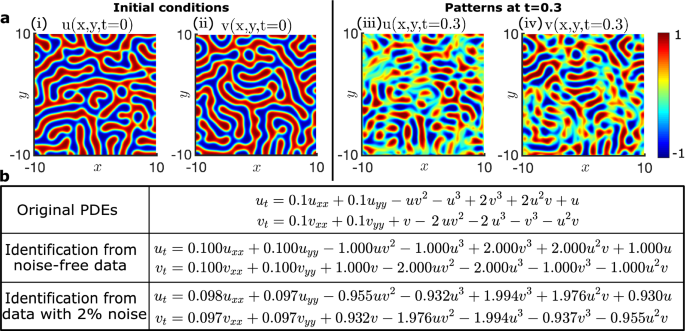
最后，我们用ATSBL演示了pde的数据驱动发现。反应-扩散方程作为生物化学系统中模式形成的原型模型引起了人们的兴趣，其中成分通过化学反应在局部相互转化，并通过扩散在空间中传输。这里，我们考虑的是受欢迎的ω\ \λ- \ \)系统，由

在哪里β\ (\ \)等于2。考虑具有周期性边界条件的二维平面矩形区域。的初始值u而且v如图所示。5-ⅰ,二世。用谱法数值求解了反应扩散方程。的快照u而且v如图所示。5a-iii iv。对于控制偏微分方程的推断，一个库矩阵\ ({\ varvec{\θ}}\)的时间导数包含35项\ (u \)而且\ \ (v)．然后，利用ATSBL，从模拟数据中推导出反应扩散方程，如图所示。5b.对于无噪声数据，识别出的方程仅在小数点后第四位与原始方程有偏差，这是由于离散化造成的。然而,如果u而且v被加性噪声破坏，识别正确的偏微分方程变得具有挑战性⁴．在裁判。⁴，因此有人建议在推理步骤之前包含去噪步骤。因此，我们采用了曲线去噪方法⁴²，可以用ATSBL从2%噪声的数据重构反应扩散方程，如图所示。5b。

数据驱动的控制方程的自动发现已经成为研究复杂系统的可行工具，如果第一原理推导是难以处理的，例如，对于生物系统或流行病学数据。这里的目标通常是构建一个分析模型，描述所观察到的动力学，并扩展到难以通过实验访问的参数空间和相空间区域。

我们的主要贡献是一种推理方法，它利用贝叶斯框架中的拉普拉斯先验分布来找到最小的控制方程集，而不需要用户输入。我们建立了该方法的有效性，并与其他方法进行了比较。对于langevin型sde的数据驱动发现，我们表明所提出的稀疏方法比基于岭回归的其他方法收敛得更快。本文不考虑SDEs中参数估计的最大似然方法，参见参考文献。⁸这些方法的介绍。对于所研究的Langevin sde，我们发现只有在相空间采样稀疏的情况下，才有利于轨迹数据的漂移和扩散系数的推断。在这种情况下，由于概率的相对不确定性不同，推断过程的误差可能在相空间中变化很大。过滤过程包括排除高不确定性的数据，结果显著提高了推理精度。

接下来，我们研究了当由于轨迹被困在局部能量极小值而难以对全局动力学进行直接推断时，主动学习过程如何有用。这一问题可以通过完善的伞状采样方法来解决，该方法采用二次偏置势来减少原始势景中的能量势垒^18，43．然而，这种偏置电位的适当参数化可能具有挑战性。例如，如果偏置势是为了平滑未知的、粗糙的能量景观。相反，我们采用数据驱动的控制方程识别方法来计算与时间相关的外部扰动，迫使轨迹探索完整的相空间。我们的方法的主要特点是，决定施加扰动的参数对应于定义能量格局的参数。将迭代推理与系统扰动相结合，可以显著提高整个推理过程的速度和准确性。因此，我们希望建议的主动学习过程将扩展数据驱动方法的适用性，特别是在计算机模拟的背景下。

与改进基于库的分析模型识别方法相关的一个核心挑战是找到自动的方法来根据手头的问题定制所使用的函数空间。最近的方法学进展表明，一种可能的解决方案是将物理约束，如对称性、守恒定律，甚至热力学，整合到控制方程的统计学习的通用框架中⁴⁴．因此，在未来几年，数据驱动的分析模型识别有可能成为缩小非参数、经验建模和基于第一性原理建模之间差距的流行工具。