简介

在研究流动不稳定性时，人们普遍认为具有屈折速度剖面的流动通常具有增长速度较强的无粘不稳定性，为快速层流-湍流过渡铺平了道路。理论支持可以追溯到瑞利的无粘理论1，以及Fjørtoft的改进判据2．两者都假设稳定性方程(无粘性Orr-Sommerfeld方程)中存在无粘性扰动，并允许基流是粘性但不可压缩的。拐点判据，虽然形式上只是作为无粘性不稳定性的必要条件，但仅仅通过观察构成经典流体力学稳定性专著基石的基流速度分布，就可以得到实质性和直观的理解3.，4．拐点准则的成功扩展到对各种控制策略的机制的感知，例如，压力梯度，壁面吸力和吹气，以及壁面加热和冷却由基流速度剖面的改变引起5．具体地说，二维基流的一般无维边界层方程如下:由粘度和密度不等的流体的流向动量导出:

$$\begin{aligned} \begin{aligned} \frac{\partial y^{2}}=&\frac{Re}{\mu}\rho u\frac{\partial u}{\partial x}+\underset{\text {gradient}}{\underset{\text {pressure}}{\underbrace{\frac{Re}{\mu}\frac{dp}{dx}}}}+\underset{\text{吹气}}{\underset{\ frac{Re}{\mu}\rho v\frac{\partial u}{\partial y}}}}-\underset{\text {cooling}}{\underset{\text {heating}/}{\underbrace{\frac{1}{\mu}\frac{\partial \mu}{\partial y}\frac{\partial u}{\partial u}{\partial y {\partial y}}}}。结束\{对齐}\{对齐}$ $
(1）

在本文中，u，v，w用于按流(x)， wall-normal (y)和展向(z)速度分量。p而且\μ(\ \)表示压力和动态粘度。所有变量都没有量纲化，有固定的参考值和压力\((\rho u^2)_{\text {ref}}\)使用。再保险是基于参考值的固定雷诺数，和\μ(\ \)而且ρ\ (\ \)是相同的，如果粘度和密度相对于它们的参考值没有改变，这是不可压缩流的标准情况。下标w用于壁面参数。使用(1)，其中一个结论是，对于标准Blasius(平板)边界层(无压力梯度，控制或传热)，\({\partial ^{2}u}/{\partial y^{2}}|_w=0\)，表示拐点严格落在壁面上;因此不存在无粘不稳定性。进一步得出，在控制后，有利压力梯度(\ (dp / dx < 0 \))、壁式抽吸(\ (v_w < 0 \))，或理想气体冷却壁(\(\partial \mu /\partial y|_w>0\))在壁面内改变拐点，使速度剖面更饱满。流因此线性更稳定(反之亦然)。当稳定性考虑中包括摩擦时，粘性Orr-Sommerfeld (O-S)方程结果为(对于给定的基流剖面u（y),w（y)，在给定x而且再保险一个是空间增长率\ (alpha _i \ \)和顺流波数\ (alpha _r \ \)固定频率的扰动在x-direction，参见公式描述。（5)及(6)．黏性不稳定补充，不需要拐点的速度分布，比无黏性不稳定弱得多，上述发现同样成立。虽然O-S框架被研究人员和工程师广泛使用，但我们应该注意到，在流体本身带来的热力学方面，它本质上忽略了物理学。因此，传统水动力稳定性理论的完整性和真实性尚不明确。

目前的工作是研究牛顿流体，即粘度不取决于流动中的剪切，而是取决于流体的温度、密度或压力的流体。我们顺便注意到非牛顿的黏弹性流动不稳定性6相当于一个自己的主题，见证了日常生活和工业中的基本应用(例如血液流动，保健产品，工程油墨)。最引人注目的特性之一是支持不稳定的雷诺数可以显著低于牛顿流。《福布斯》(Forbes)的研究提供了一些早期证据7他提出，即使是弱的非牛顿效应也会导致不稳定。

图1
图1

（一个)概述建立一般流动稳定性分析框架的基本输入。灰色背景环绕着经典的O-S框架，其中只有雷诺数和速度剖面承载物理特性。（b中定常横流模式的稳定性图β\ (x - \ \)框架。空间增长率\(- \α_i \)(黑线)和N因子(白线)比较完整(实线)和O-S(虚线)方程。

全尺寸图像

结果

非理想流体流动不稳定性的一般框架概述

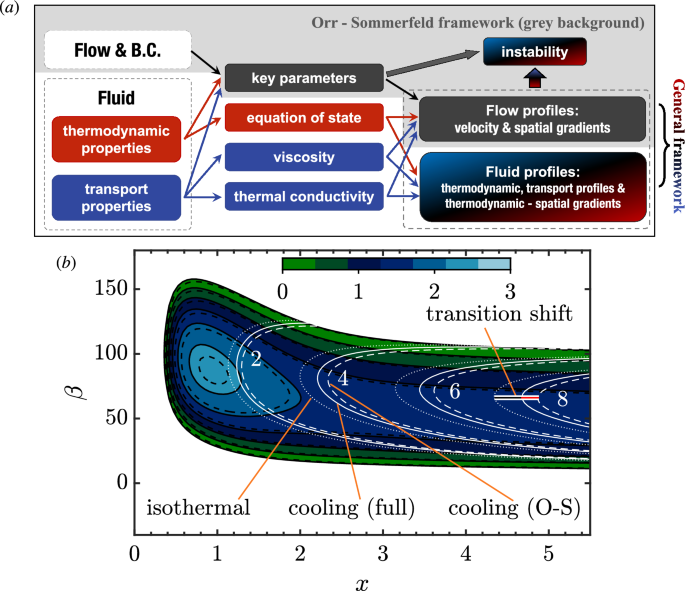
数字1A封装了流的线性稳定性分析的组成输入。该问题由流量和流动流体共同定义。在传统的O-S框架中，流体被假定为不可压缩的、理想的和等温的，因此能量方程被省略，流体的物理作用因此被最小化。有兴趣的读者请参阅Eq (6)的“方法”一节。假设不可压缩流体和完美气体，经典稳定性理论解决了一个简化的特征值问题。在一般框架下，除了速度剖面，状态变量关系(状态方程)和传输剖面(粘度和热导率)以及它们的热力学梯度成为稳定性问题的重要输入。此外，流体的性质也改变了速度分布(正如经典框架所解释的)。所有关键参数，如雷诺数、马赫数、普朗特数和埃克特数，都相应地取决于流体性质。将此一般观点与Eq. (1)，压力梯度和壁面吸吹的参与(1)在O-S框架内。然而，使用拐点准则来解释壁面冷却/加热的影响是不明确的。原因是壁面冷却/加热不仅影响速度分布，而且还需要整合流体的固有物理，特别是在稳定性方程中。作为一个例子，我们考虑三维边界层流动的稳定性，因为这是能量转换机旋转叶片上流动的最具代表性的8．两种根本不同的不稳定性可以发生-交叉流(CF)和tollmien - schlichting型(TS)不稳定性。主稳定性性质的改变不仅会导致过渡位置的改变，而且会导致不同的过渡机制和控制措施9．基流对应于(理想空气)实验10，11并模拟机翼表面受有利压力梯度影响的低速掠流，其中CF模式(综合评论可通过12，13)是层流-湍流转变的原因。研究人员和工程师依靠生长速率的积分——N因子——来确定过渡位置14．数字1b比较理想气体的完全稳定方程(实线)与具有恒定密度和粘度的标准O-S设置(虚线)之间的稳定CF模式的增长率和N因子。因子N等于从所考虑扰动的中性位置开始的空间增长率的积分:

$$\begin{aligned} {N=\mathop {{\mathop {\intop}\nolimits _{\left。x \ | _{\α_{我}= 0}}^ {x}}} \限制(α- \ _{我})文本\ d {} x;\;-\alpha _i=\frac{\text {d}}{\text {d}x}\ln (A)， \text{其中A \text{是扰动的幅度。}} \end{aligned}$$
(2)

流动受到壁面冷却的影响\ (T_w / T_ \ infty = 15/16 \识别)．我们展示了n因子值为2、4、6和8的等值线，其中包括不受控制的等温参考情况(虚线)，以表明壁面冷却的效果。可以看出，如果用风洞测量\ (N = 8 \)为了表明转变开始，等温箱有一个转变位置文本\(间\ {iso} = 4.34 \)．考虑壁面冷却，完整方程给出了过渡位移\(\Delta x_\text{full} = 0.33\)而经典的O-S设定预测\(\Delta x_\math {O-S} = 0.52\)比正确的过渡位移多58.8%因此，使用经典的O-S框架大大高估了壁面冷却的影响，因为稳定性方程中的热力学和输运性质影响部分补偿了改变的基流剖面的影响。

作为构建更物理系统的重要一步，李斯和林15导出了考虑流动温度贡献的可压缩流动广义拐点判据。麦克16提出了可压缩流动的粘性理论。他发现当马赫数增加时，稳定方程的数学性质发生了变化，导致了著名的麦克高模态(通常主导高超声速流动的流动过渡)。然而，在可压缩方案中，由于以前的气动要求，流体的物理性质在很大程度上停留在理想气体状态。另一方面，O-S框架已经扩展到考虑温度依赖性粘度17，18，结合多种控制方式19．与对粘度的强调一致，粘度分层流动是一种特别引人注意的类型20.．例如，它们的不稳定性已经揭示了水平热平流的流动21，混溶流体的混合层22，23．沿着不同的路径走向湍流24时，黏度分层对代数失稳的影响最小25．相反，黏度梯度显著地改变了边缘状态，导致了过渡阈值的改变26．从无花果上看。1第一，粘度只是真正流体物理的一部分27，28．另一种是状态变量关系，如果压力较高，分子间作用力对流体行为有直接影响，则会引起非理想流体性质的影响，也称为实气效应。基于理想气体假设的稳定性框架，在提供非理想基流剖面的前提下，能否给出正确的预测?我们的目标是通过这篇文章来回答这个问题，这应该引起人们的注意，将热力学整合到水动力稳定性理论中，并有助于更好地理解具有实质性流体的流动，例如血液流动29，地球物理流30.，31，超流体湍流32密集流33．

图2
图2

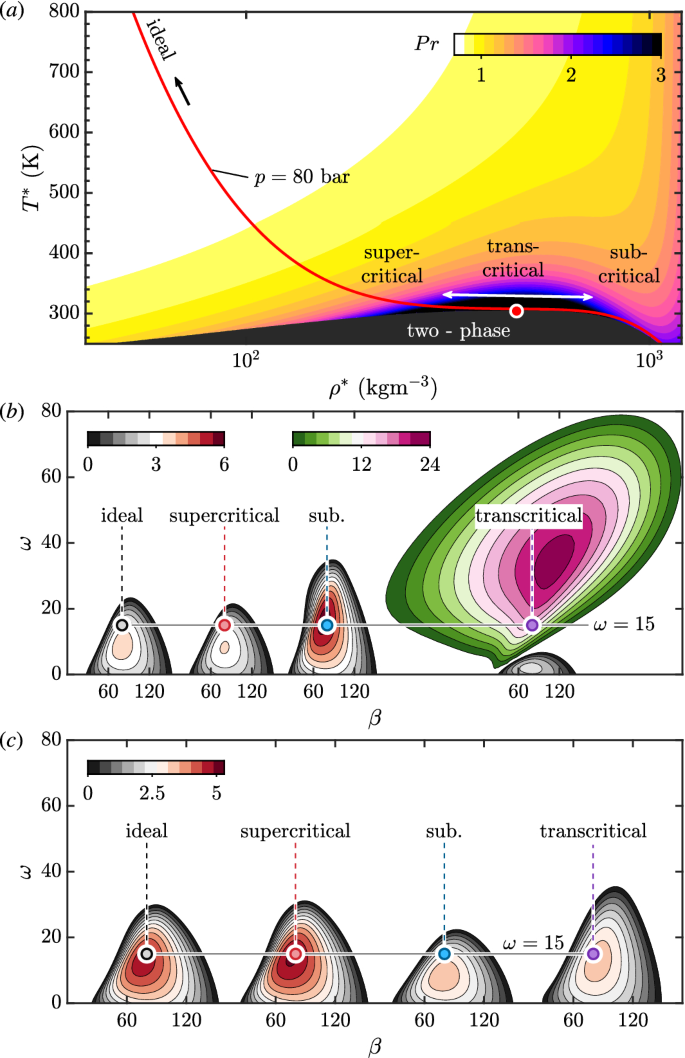
（一个)用普朗特数着色的CO2温度-密度图。红色实线对应的等压线为80，在等压线附近考虑三维边界层。红点标志着靠近Widom线的临界点;可以看到理想的、超临界的、跨临界的和次临界的体制。（b，c)不同状态下的稳定性图(b)壁面冷却及(c)在ω\ \β- \ \)框架。面板内(b)中，我们使用了一个单独的彩色图来表示无粘性的Tollmien-Schlichting模式(最右)，它的增长速度明显更大。彩色的圆点表示模态不稳定\(β= 80 \ \)而且\ \(ω= 15 \)在图中讨论。3.．

全尺寸图像

超临界CO的三维边界层不稳定性2

在不失一般性的前提下，我们考虑临界点附近的超临界流体。这些流体被认为是能源部门的重要工作介质8，而它们高度非理想的热力学和输运性质挑战了传统的框架。数字2A为温度-密度(\ (T -ρ\ \))产地来源证图表2普朗特数着色(\ (Pr = \μC_p / \ kappa \))．\ (C_p \)而且\ (\ kappa \)分别代表等压比热容和热导率。我们将重点关注80等压线，沿该等压线在越过伪临界点(与临界压力处的临界点重合)时发生强烈的非理想性，也称为Widom线34这是伪沸腾的物理特征，定义为的等压最大值\ (C_p \)．图中报告了理想状态。1a对应高温状态(600k以上)，可以看出，普朗特数仅在理想状态下为常数，在临界点附近有较强的变化，高度依赖于热力学状态。用这种流体和它的热力学性质的查表35的三维边界层稳定图β\ \ω- \ \)框架\ (x = 1 \)在无花果。2B和c分别用于墙壁冷却和加热。一个清晰的对比表明，壁面冷却/加热的效果高度依赖于流体的热力学状态。例如，在跨临界区，流支持另一种具有巨大增长速率和不稳定带的模式。该模式为无粘性Tollmien-Schlichting (/ Kelvin-Helmholtz)型，即波相速度大约朝向主流方向放大最大，在压力梯度不利时可以预期，而在压力梯度有利时则完全不可能9．尽管存在有利的压力梯度，但由于存在来自微小表面粗糙度的稳定CF涡，这里将出现ts型流动过渡，而不是CF型过渡。这一戏剧性的差异表明，在整合热力学时出现了新的物理学。此外，壁热效应在超临界区增强，但在亚临界区和跨临界区不明显。是什么导致了如此大的差异，基流速度或图中所示的其他项目。1一个吗?

图3
图3

图中彩色点对应的线性稳定性的离散谱。2B和c，\(\beta =80，~\omega =15\)．面板(一个)为Fig。2B、冷却壁、面板(b)为无花果。2C、采暖墙。我们考虑了在理想状态下冻结某些输入和O-S方程的影响。结果用小实心圆表示，并标注了生长速率的误差。在三种非理想状态(红色、蓝色、品红)中，我们使用理想粘度和热导率输入来表示影响。（c)w，ρ\ (\ \)，\(\partial p/\partial T\),\(\partial \mu /\partial \rho\)作为函数y对于冷却墙来说。它们属于源于状态变量关系和输运性质的速度、密度剖面和热力学梯度(图2)。1一个)。

全尺寸图像
图4
图4

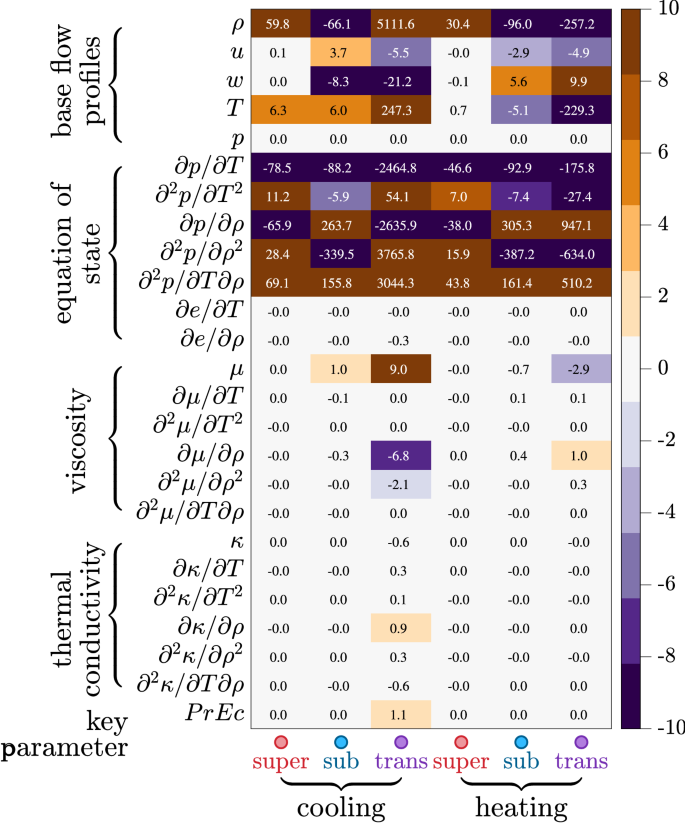
灵敏度\ε(\ \)的空间增长率到不同的稳定算子的输入。这些输入对应于图中所示的不同类别。1a.六列分别为具有壁面冷却和加热条件的超临界、亚临界和跨临界状态(见图底)。

全尺寸图像

非理想性的作用

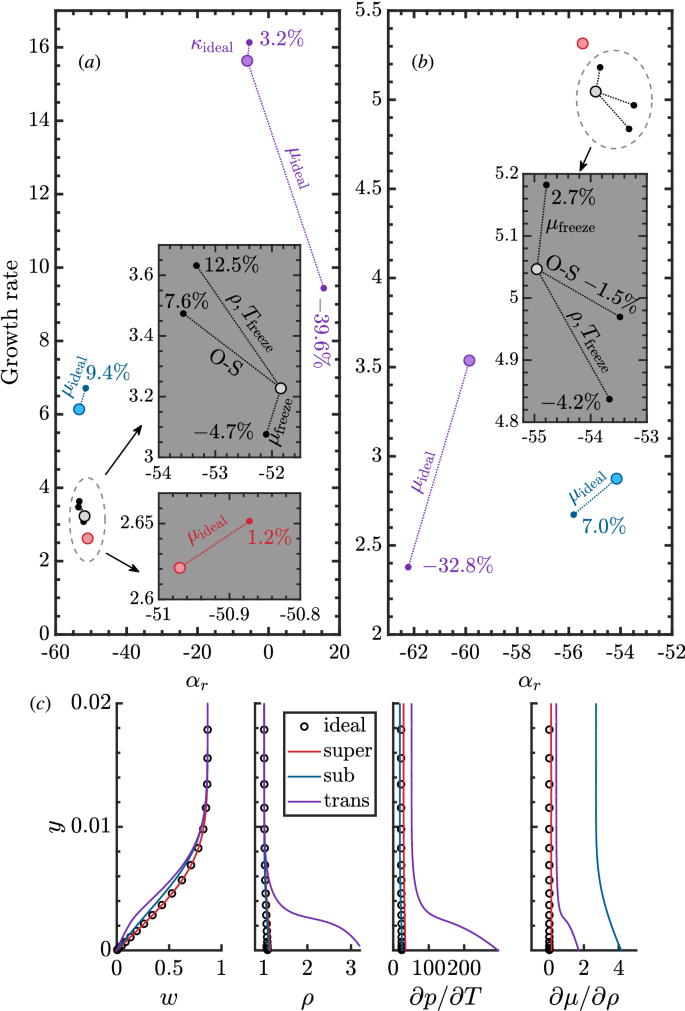
数字3.A和b比较了稳定图中的代表性模态，\(β= 80 \ \)而且\ \(ω= 15 \)，分别用于墙壁冷却和加热。空间增长率\(- \α_i \)和波数\ (alpha _r \ \)会显示出来。颜色样式与图相匹配。2B和c，贯穿整个文章，表示不同的热力学状态。理想状态的放大显示了不同的简化对结果的偏差。例如，O-S框架导致墙体冷却/加热的增长率误差为7.6%/−1.5%。单独冻结粘度曲线或密度-温度曲线也会导致显著的特征值变化，这表明即使是理想气体，一旦存在温度梯度，用简化的框架也无法得到准确的n因子。考虑到传统的稳定性框架对输运性质采用经验定律，我们表明，以非理想基流作为输入，使用该框架是不够的。特别是，通过替换粘度(\μ(\ \)和相关梯度)与理想定律(例如，萨瑟兰定律)。我们还应注意到，热导率(\ (\ kappa \)和相关的梯度)要小得多，只有在冷却的跨临界状态下才显得至关重要。

除了输运特性，图;3.C比较基流配置文件w，ρ\ (\ \)，\(\partial p/\partial T\)，\(\partial \mu /\partial \rho\)．值得注意的是，速度剖面(w（y)在不同的热力学状态下发生变化。特别是在壁面冷却的跨临界情况下，在壁面附近出现了一个拐点，伴随着强烈的密度变化，导致无粘TS不稳定。为了全面地理解流体的热力学作用，我们提出了灵敏度\ε(\ \)的增长率对稳定性方程的每个输入，定义为

$$\begin{aligned} \varepsilon =\left。\frac{\partial \alpha}{\partial \sigma}\right| _{\sigma \rightarrow 0}，\ chi =\sigma \chi _{\text{理想}}+\left(1-\sigma \right) \chi _{\text{非理想}}\end{aligned}$$
(3)

在这里\气(\ \)表示任何物理输入，例如:T而且\(\partial \mu /\partial \rho\)．因此，灵敏度测量稳定性如何依赖于相对于传统理想假设的非理想输入。数字4展示了在不同热力学状态下每一项的摘要。对于所有非理想状态，得出的第一个结论是:速度和热力学轮廓和梯度发挥最关键的影响(除压力外，表的前10行)，而输运特性，如图所示。3.A和b的影响较小，尽管它们已经显示出显著的影响(粘度相关术语)。因此，必须考虑流体的所有热力学物理(包括输运性质)，以正确地获得基本剖面(例如，ρ\ (\ \)，u，T，\(\partial p/\partial T\))．无花果选人。4一列一列地总结，跨临界制度具有最高的敏感性。这是由于它的最实质的非理想越过智慧线。同样值得注意的是，像\(\partial \mu /\partial \rho\)而且\(\partial \kappa /\partial \rho\)在传统研究中通常被忽略。因此，即使有正确的基流剖面，水动力稳定性框架也必须升级，以纳入所有相关剖面，除非在实际情况下满足理想气体假设。

讨论

我们的研究强调了当所研究的剪切层存在温度梯度时，准确地包括常规水动力稳定性理论中遗漏的(非理想)流体的热力学性质的重要性。更普遍的情况是，当流体在其临界点附近运行时，存在高度非理想的热力学效应，传统框架无法给出正确的增长速度、主导模式，从而无法预测过渡物理，这可能会使预先设计的控制措施变得毫无意义。灵敏度研究表明，热力学，即状态变量关系(状态方程)和粘度(包括其热力学梯度)，而不是热导率，必须在基流剖面中充分考虑而且水动力稳定框架。这也意味着使用近似的，解析的状态方程，如范德华模型或其他27可能会明显恶化稳定性结果。

方法

层流基流

我们求解了层流基流的“抛物线化”Navier-Stokes方程(PNS)。在无分离的稳态边界层流动中，沿流方向的黏性梯度比沿壁法线方向的黏性梯度小得多。因此，PNS由完整的Navier-Stokes方程导出，在粘性项中去掉了顺流梯度36．

我们使用下标e对于边界层边缘值。在这里\(\rho _{e}\左(x\右)\)而且\ (T_ {e} \识别左(x \) \)势/非旋转流量值是否由等熵关系给出:

$ $ \{对齐}开始年代\离开(\ρ_ {e} \离开(x \右),p \左(x \) \右)左= S \ \ρ_ {\ infty}, p_ ({\ infty} \右),\;S \离开(T_ {e} \识别(x \右),p \左(x \) \右)= S \离开(T_ {\ infty},识别p_ {\ infty} \右),\{对齐}$ $
(4)

在哪里年代代表熵，和p（x)为测得的压力\ (dp / dx < 0 \)．PNS采用隐式欧拉方案集成在下游，从初始剖面开始\ (x = x_0 \)．在本研究中，我们规定了流向速度和展向速度\ (u (x_0, y) \)，\ (w(从y) \)使用Falkner-Skan-Cooke (FSC)解决方案和\ (v(从y) = 0 \)．热力学变量(\(\rho, T\))可以作为势流量值(应用等熵关系)给出，也可以从现有下游数据中推断出来。对不同初始轮廓的PNS结果进行了验证，确保初始轮廓的影响不显著。

线性稳定性，完全包括热力学

我们考虑了层流基流的线性模态不稳定性。该理论基于状态假设，即一个简单的可压缩系统是由两个独立的热力学性质定义的。摄动向量定义为\ ({\ varvec {q}} = \离开(\ρ^ {\ '},u ^ {\ '}, v ^ {\ '}, w ^ {\ '}, T ^{\ '} \右)^ {T} \)．因此，其他输运和热力学性质的扰动(例如，\ (e ^ {\ '} \)，\(\kappa ^{\prime}\)的函数\((\rho ^{\prime}，T^{\prime})\)二维泰勒展开37．稳定性方程由N-S方程减去未扰动基流的控制方程得到，公式为

$ $ \开始{对齐}{\ varvec {\ mathsf {{L}}}} _ {\ varvec {\ mathsf {{t}}}} \压裂{\部分{\ varvec {q}}}{\部分t} + {\ varvec {\ mathsf {{L}}}} _ {\ varvec {\ mathsf {{x}}}} \压裂{\部分{\ varvec {q}}} {x} \部分+ {\ varvec {\ mathsf {{L}}}} _ {\ varvec {\ mathsf {{y}}}} \压裂{\部分{\ varvec {q}}}{\偏y} + {\ varvec {\ mathsf {{L}}}} _ {\ varvec {\ mathsf {{z}}}} \压裂{\部分{\ varvec {q}}}{\部分z} + {\ varvec {\ mathsf {{L}}}} _ {\ varvec {\ mathsf {{q}}}} {\ varvec {q}} + {\ varvec {\ mathsf {{V}}}} _ {{\ varvec {\ mathsf {{xx}}}}} \压裂{\部分^ {2}{\ varvec {q}}}{\部分x ^ {2}} + {\ varvec {\ mathsf {{V}}}} _ {{\ varvec {\ mathsf {{xy}}}}} \压裂{\部分^ {2}{\ varvec {q}}}{\部分x \偏y} + {\ varvec {\ mathsf {{V}}}} _ {{\ varvec {\ mathsf {{xz}}}}} \压裂{\部分^ {2}{\ varvec {q}}}{\部分x \部分z} + {\ varvec {\ mathsf {{V}}}} _ {{\ varvec {\ mathsf {{yy}}}}} \压裂{\部分^ {2}{\ varvec {q}}}{\偏y ^ {2}} + {\ varvec {\ mathsf {{V}}}} _ {{\ varvec {\ mathsf {{yz}}}}} \压裂{\部分^ {2}{\ varvec {q}}}{\偏y \部分z} + {\ varvec {\ mathsf {{V}}}} _ {{\ varvec {\ mathsf {{zz}}}}} \压裂{\部分^ {2}{\ varvec {q}}}{\部分z ^{2}} = 0。\{对齐}$ $
(5)

式中矩阵的定义(5)在ref中提供27．常态形式，\ ({\ varvec {q}} \离开(x, y, z, t \右)= \帽子{{\ varvec {q}}} \左(y \) \ exp \左(我\ \αx +βzi \ωt \右)+运费到付。\)，我们求空间模式下的解，其中展向波数β\ (\ \)和角频率ω\ (\ \)都是实际输入\α(\ \)复特征值是否由由此产生的非线性特征值问题确定:

$ $ \开始{对齐}{\ varvec {\ mathsf {{L}}}} \帽子{{\ varvec {q}}} = 0。\{对齐}$ $
(6)

在这里\ ({\ varvec {\ mathsf {{L}}}} \)是一个5 × 5矩阵。其具体表达式为:

$ $ \{对齐的开始 }{} & {} {\ varvec {\ mathsf {{L}}}} _{1 1} =α- i \ u + iβ\ω- i \ w \; {\ varvec {\ mathsf {{L}}}} _{1,2} =ρα- i \ \ \; {\ varvec {\ mathsf {{L}}}} _{1,3} = - \ρD - \压裂{\部分\ρ}{\偏y} \; {\ varvec {\ mathsf {{L}}}} _{1 4} =β-我\ \ρ,\;{\ varvec {\ mathsf {{L}}}} _{1, 5} = 0 \{对齐}$ $
(7）
$ $ \{对齐的开始 }{} & {} {\ varvec {\ mathsf {{L}}}} _{2, 1} =α- i \ \压裂{\部分p}{\部分\ρ}+ \压裂{1}{你}\压裂{\部分\μ}{\部分\ρ}\压裂{\偏u}{\偏y} D + \压裂{1}{你}\压裂{\部分\μ}{\部分\ρ}\压裂部分^ {\ u}{2}{\偏y ^{2}} + \压裂{1}{你}\压裂{\偏u}{\偏y} \离开(\压裂{\部分^{2}\μ}{\部分\ρ^{2}}\压裂{\部分\ρ}{\偏y} + \压裂{\部分^{2}\μ}{\部分\ρ\部分T} \压裂{\部分T}{\偏y} \) \{对齐}$ $
（8）
$ $ \{对齐的开始 }{} & {} {\ varvec {\ mathsf {{L}}}} _{2,} = - \压裂{\α^{2}\离开(2 \μ+ \λ\右)}{你}ρα- i \ \ u + i \ω\ρ+ \压裂{1}{你}\压裂{\部分\μ}{\偏y} \β\ w +ρ\ D - i压裂{\μ}{你}D ^{2} - \压裂{\β^{2}\μ}{你}\{对齐}$ $
（9)
$ $ \{对齐的开始 }{} & {} {\ varvec {\ mathsf {{L}}}} _{2,3} = \压裂{我\α\ \μ+ \λ\右)D}{你}+ \压裂{\α}{你}\压裂{\部分\μ}{\偏y} - \ρ\压裂{\偏u}{\偏y}, \; {\ varvec {\ mathsf {{L}}}} _{2,4} = - \压裂{\α、β\离开(\μ+ \λ\右)}{你}\{对齐}$ $
(10)
$ $ \{对齐的开始 }{} & {} {\ varvec {\ mathsf {{L}}}} _{2、5}=α- i \ \压裂{\部分p}{\部分T} + \压裂{1}{你}\压裂{\部分\μ}{\部分T} \压裂{\偏u}{\偏y} D + \压裂{1}{你}\压裂{\部分\μ}{\部分T} \压裂部分^ {\ u}{2}{\偏y ^{2}} + \压裂{1}{你}\压裂{\偏u}{\偏y} \离开(\压裂{\部分^{2}\μ}{\部分T ^{2}} \压裂{\部分T}{\偏y} + \压裂{\部分^{2}\μ}{\部分T \部分\ρ}\压裂{\部分\ρ}{\偏y} \) \{对齐}$ $
（11）
$$\begin{aligned}{} & {} {\varvec{\mathsf{{L}}}}_{3,1}=\frac{i\alpha}{Re}\frac{\partial \mu}{\partial \rho}\frac{\partial \ u}{\partial y}-\frac{\partial \frac{\partial \mu}{\partial \rho}\frac{1}{Re}\frac{\partial \mu}{\partial \rho}\frac{\partial \rho ^{2}p}{\partial \rho ^{2}}\frac{\partial \rho}{\partial y}-\frac{\partial \ {2}p}{\partial \rho \partial T}\frac{\partial T}{\partial y}\end{aligned}$$
（12）
$ $ \{对齐的开始 }{} & {} {\ varvec {\ mathsf {{L}}}} _{3 2} = \压裂{我\α\ \μ+ \λ\右)D}{你}+ \压裂{\α}{你}\压裂{\部分\λ}{\偏y} \; {\ varvec {\ mathsf {{L}}}} _{3、4}=我\β\压裂{1}{你}\压裂{\部分\λ}{\偏y} + \压裂{我\β\ \μ+ \λ\右)D}{你}\{对齐}$ $
（13）
$ $ \{对齐的开始 }{} & {} {\ varvec {\ mathsf {{L}}}} _{3 3} = - \压裂{\α^{2}\μ}{你}ρα- i \ \ u + i \ω\ρ+ \压裂{1}{你}\压裂{\部分\离开(2 \μ+ \λ\右)}{\偏y} \β\ w +ρ\ D - i压裂{2 \μ+ \λ}{你}D ^{2} - \压裂{\β^{2}\μ}{你}\{对齐}$ $
(14）
$$\begin{aligned}{} & {} {\varvec{\mathsf{{L}}}}_{3,5}=\frac{i\alpha}{Re}\frac{\partial \mu}{\partial T}\frac{\partial u}{\partial y}-\frac{\ \frac{\partial \mu}{\partial T}\frac{\partial w}{\partial y}-\frac{\partial ^{2}p}{\partial T^{2}}\frac{\partial T}{\partial y}\ frac{\partial ^{2}p}{\partial \rho \partial T}\frac{\partial \rho}{\partial y}\ frac{\partial ^{2}p}{\partial \rho \partial T}\frac{\partial \rho}\end{aligned}$$
(15）
$ $ \{对齐的开始 }{} & {} {\ varvec {\ mathsf {{L}}}} _{4 1} = \压裂{1}{你}\压裂{\部分\μ}{\部分\ρ}\压裂{\部分w}{\偏y} \β\ d - i压裂{\部分p}{\部分\ρ}+ \压裂{1}{你}\压裂{\部分\μ}{\部分\ρ}\压裂部分^ {\ w}{2}{\偏y ^{2}} + \压裂{1}{你}\压裂{\部分w}{\偏y} \离开(\压裂{\部分^{2}\μ}{\部分\ρ^{2}}\压裂{\部分\ρ}{\偏y} + \压裂{\部分^{2}\μ}{\部分\ρ\部分T} \压裂{\部分T}{\偏y} \) \{对齐}$ $
（16）
$ $ \{对齐的开始 }{} & {} {\ varvec {\ mathsf {{L}}}} _{4,2} = - \压裂{\α、β\离开(\μ+ \λ\右)},{你}\;{\ varvec {\ mathsf {{L}}}} _{4 3} =我\β\压裂{1}{你}\压裂{\部分\μ}{\偏y} + \压裂{我\β\ \μ+ \λ\右)D}{你}- \ρ\压裂{\部分w}{\偏y} \{对齐}$ $
(17)
$ $ \{对齐的开始 }{} & {} {\ varvec {\ mathsf {{L}}}} _{4 4} = - \压裂{\α^{2}\μ}{你}ρα- i \ \ u + i \ω\ρ+ \压裂{1}{你}\压裂{\部分\μ}{\偏y} \β\ w +ρ\ D - i压裂{\μ}{你}D ^{2} - \压裂{\β^{2}\离开(2 \μ+ \λ\右)}{你}\{对齐}$ $
（18)
$ $ \{对齐的开始 }{} & {} {\ varvec {\ mathsf {{L}}}} _{4、5}= \压裂{1}{你}\压裂{\部分\μ}{\部分T} \压裂{\部分w}{\偏y} \β\ d - i压裂{\部分p}{\部分T} + \压裂{1}{你}\压裂{\部分\μ}{\部分T} \压裂部分^ {\ w}{2}{\偏y ^{2}} + \压裂{1}{你}\压裂{\部分w}{\偏y} \离开(\压裂{\部分^{2}\μ}{\部分T ^{2}} \压裂{\部分T}{\偏y} + \压裂{\部分^{2}\μ}{\部分T \部分\ρ}\压裂{\部分\ρ}{\偏y} \) \{对齐}$ $
(19)
$ $ \开始{对齐}{}{}{\ varvec {\ mathsf {{L}}}} _{5 1} & =ρα- i \ \ u \压裂{\部分e}{\部分\ρ}+ i \ω\ρ\压裂{\部分e}{\部分\ρ}+ \压裂{1}{RePrEc} \压裂{\部分\ kappa}{\部分\ρ}\压裂{\部分T}{\偏y} \β\ρw \ d - i压裂{\部分e}{\部分\ρ}\ nonumber \ \{} & \四{}+ \压裂{1}{RePrEc}左(\ \压裂{\部分\ kappa}{\部分\ρ}\压裂{\部分^ T}{2}{\偏y ^{2}} + \压裂{\部分^ {2}\ kappa}{\部分\ρ^{2}}\压裂{\部分\ρ}{\部分\frac{\partial T}{\partial y}+\frac{\partial ^{2}\kappa}{\partial \rho \partial T}\左(\frac{\partial T}{\partial y}\右)^{1}{Re}\frac{\partial \mu}{\partial \rho}\左(\左(\frac{\partial u}{\partial y}\右)^{2}+\左(\frac{\partial w}{\partial y}\右)^{2}\右)\end{aligned}$$
(20)
$ $ \{对齐的开始 }{} & {} {\ varvec {\ mathsf {{L}}}} _ {5, 2} = - i \αp + \压裂{2 \μ}{你}\压裂{\偏u}{\偏y} D \; {\ varvec {\ mathsf {{L}}}} _{5 3} = \压裂{2μα我\ \}{你}\压裂{\偏u}{\偏y} pd + i \β\压裂{2 \μ}{你}\压裂{\部分w}{\偏y} - \ρ\压裂{\部分e}{\偏y} \; {\ varvec {\ mathsf {{L}}}} _{5 4} = \压裂{2 \μ}{你}\压裂{\部分w}{\偏y} \ D - iβ\ p{对齐}$ $结束
(21)
$$\begin{aligned}{} {} {\varvec{\mathsf{{L}}}}_{5,5}&= -\frac{\alpha ^{2}\kappa}{\partial e}{\partial T}+i\omega \rho \frac{\partial e}{\partial y}+\frac{\partial T}\frac{\ \kappa}{\partial y}\right) D-i\beta \rho w\frac{\partial e}{\partial T}+ frac{\kappa}{RePrEc}D^{2}-\frac{\ \kappa \beta ^{2}}{RePrEc}\ nonnumber \\{} & {} \quad +\frac{1}{RePrEc}\left(\frac{\partial \kappa}{\ \partial kappa}{\ \partialT}\frac{\partial ^{2}T}{\partial y^{2}}+\frac{\partial ^{2}\kappa}{\partial T}\{2}}\左(\frac{\partial T}{\partial y}\右)^{2}+\frac{\partial ^{2}\kappa}{\partial rho \partial T}\frac{\partial T}{\partial y}\右)+\frac{1}{Re}\frac{\partial \mu}{\partial T}\左(\左(\frac{\partial u}{\partial y}\右)^{2}+\左(\frac{\partial w}{\partial y}\右)^{2}\左{aligned}$$
(22)

在这里D为微分矩阵(使用切比雪夫谱法)\ (D \帽子{你}= D \帽子{你}/ dy \)．扰动受狄利克雷边界条件(\ (u ^ {\ '} = v ^ {\ '} = w ^ {\ '} = T ^ {\ '} = 0 \))在墙上和自由泳。与传统的LST框架相比，目前的方法已被验证在理想气体状态下重现经典结果38．正如前一节所讨论的，当流体在其临界点附近运行时，扰动的增长速率对特征值问题的输入具有极大的敏感性。因此，热力学和输运模型对于获得精确的物理结果至关重要。使用不同状态方程的比较(van der Waals, Redlich-Kwong, Peng-Robinson)27显示没有收敛的结果，即使其他模型保持不变。因此，使用一个精确的查找表来生成如图左列所示的输入4．特征值问题(6)用切比雪夫搭配点进行离散，并沿壁法向用300个网格点进行数值求解。结果已被测试为网格无关的。