乘法拓扑阶段gydF4y2Ba

寻找新的物质相态——特别是金兹堡-朗道范式之外的物质相态，被称为物质拓扑相态——现在是凝聚态物理学中一个广泛而有影响力的话题gydF4y2Ba^{1gydF4y2Ba，gydF4y2Ba2gydF4y2Ba，gydF4y2Ba3.gydF4y2Ba，gydF4y2Ba4gydF4y2Ba，gydF4y2Ba5gydF4y2Ba，gydF4y2Ba6gydF4y2Ba，gydF4y2Ba7gydF4y2Ba，gydF4y2Ba8gydF4y2Ba，gydF4y2Ba9gydF4y2Ba，gydF4y2Ba10gydF4y2Ba，gydF4y2Ba11gydF4y2Ba，gydF4y2Ba12gydF4y2Ba，gydF4y2Ba13gydF4y2Ba}．最近的研究主要集中在考虑一组扩展的保护对称gydF4y2Ba^{14gydF4y2Ba，gydF4y2Ba15gydF4y2Ba，gydF4y2Ba16gydF4y2Ba，gydF4y2Ba17gydF4y2Ba，gydF4y2Ba18gydF4y2Ba，gydF4y2Ba19gydF4y2Ba}以及在非电子的、驱动的或与环境耦合的系统中实现拓扑gydF4y2Ba^{20.gydF4y2Ba，gydF4y2Ba21gydF4y2Ba，gydF4y2Ba22gydF4y2Ba，gydF4y2Ba23gydF4y2Ba，gydF4y2Ba24gydF4y2Ba，gydF4y2Ba25gydF4y2Ba，gydF4y2Ba26gydF4y2Ba}因为我们对平衡和孤立电子拓扑的理解被认为是对有效的非相互作用系统的完整理解。gydF4y2Ba

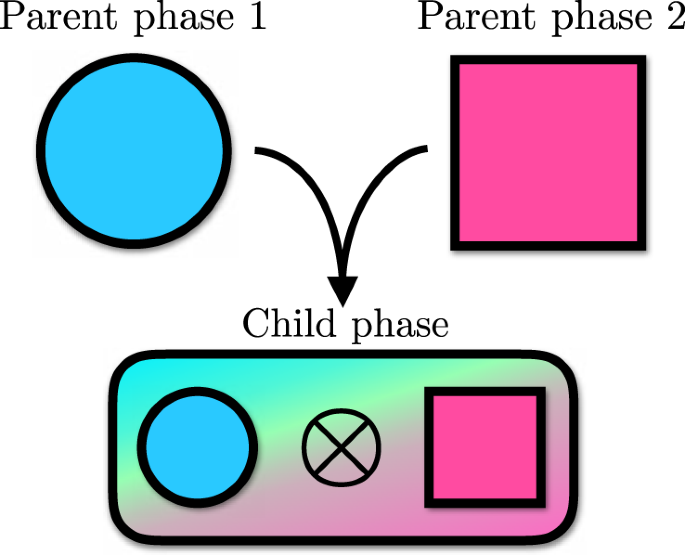
然而，我们并没有像过去那样，通过只对一个系统的整个哈密顿量施加对称来实现非平凡拓扑，而是通过对哈密顿量的分量施加对称来进行推广，这些分量是相乘组合的，即通过向量空间积而不是直接和组合。这种方法导致了构造大量以前未识别的拓扑相的方法，包括两个新相的例子，作为这些方法的概念证明，以及一个如何在该框架中查看已知相的例子。这种方法大大扩展了对称保护的物质拓扑相的可能集合，因为在研究拓扑时已经考虑到的大量对称集可以被组合，允许一组物质的父相组合成合成父相属性的单一子相，如图所示。gydF4y2Ba1gydF4y2Ba．许多这样的对称性是常见的，表明乘法拓扑可能出现在电子系统的其他情况。这种物理进一步扩展到各种非电子拓扑相和驱动或非厄米系统，扩展到每一组拓扑相。gydF4y2Ba

我们通过构造两种新的对称保护物质拓扑相，乘Hopf绝缘体和乘Chern绝缘体，来明确地演示这种方法，尽管这个概念更广泛;事实上，我们证明了在一种拓扑超导体中自然也存在一种产物结构。我们首先构建一个乘法哈密顿量的例子它是两个非简并父哈密顿量的子量，gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 1 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba而且gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 2 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba．然后，我们在介绍物质的乘性相的基本例子，乘性Hopf和Chern绝缘子(MHI和MCI)之前，证明了这种形式可能是对称保护的，因此它描述了物质的相。gydF4y2Ba

乘法哈密顿量的构造gydF4y2Ba

为了构造乘式哈密顿量，我们首先根据父哈密顿量的矩阵元素确定乘式哈密顿量的矩阵元素表达式。为了做到这一点，我们考虑由特殊酉群SU(2)的元素作用的父哈密顿量。这样的哈密顿量有两个带，可以描述物质的Chern绝缘体和Hopf绝缘体拓扑相。由这样的亲本构造的子哈密顿量将被半单李群SU(2) × SU(2)作用。由于这个李群同构于特殊正交群SO(4)的双盖，这个直接积表明存在一个从两个具有2 × 2矩阵表示的父哈密顿量到一个具有4 × 4矩阵表示的子哈密顿量的映射。gydF4y2Ba

在“用父哈密顿量表示乘子哈密顿量的方法”中给出了同构的显式构造，并给出了子哈密顿量的结果表达式。我们把gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 1 }({{{{{{{\ boldsymbol {k }}}}}}}})=({{ } \四{b} \在c{} \四{d}}) \)gydF4y2Ba而且gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 2 }({{{{{{{\ boldsymbol {k }}}}}}}})=({{\ βα}\四{\}\在{\ kappa} \四{\三角洲}})\)gydF4y2Ba为结构中的两父哈密顿量，动量依赖被抑制。的厄米性当然可以进一步简化表达式gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 1 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba而且gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 2 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba,这使gydF4y2BacgydF4y2Ba=gydF4y2BabgydF4y2Ba^＊gydF4y2Ba而且gydF4y2BaκgydF4y2Ba=gydF4y2BaβgydF4y2Ba^＊gydF4y2Ba，确保子哈密顿量的隐密性，但为了更清楚地显示子哈密顿量对父哈密顿量的潜在依赖，我们保留了更一般的表达式。我们可以写出子哈密顿量gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ c }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba而言,gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 1 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba而且gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 2 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba作为gydF4y2Ba

这种乘积形式的哈密顿量的最常见的物理例子，可能来自于可以在泡利矩阵上展开的2乘2哈密顿量，出现在二维狄拉克材料理论中，其中2乘2分量可以表示自旋、谷或层自由度。更具体地说，在这项工作中，附加的粒子空穴对称被强制用于对称保护乘法相位，可以对应于有效地拥有无纺锤版本的时间反转对称的子粒子。因此，乘相可以对应于具有适当轨道或谷自由度的无旋超导体。gydF4y2Ba

我们简要评述了乘法相和平方根拓扑相的这种张量积结构之间的区别gydF4y2Ba^{27gydF4y2Ba，gydF4y2Ba28gydF4y2Ba，gydF4y2Ba29gydF4y2Ba，gydF4y2Ba30.gydF4y2Ba}:这些过去的工作与我们的乘法结构不同，涉及到寻找布洛赫哈密顿量gydF4y2Ba\({{{{{{{\ mathcal {H }}}}}}}}({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba以非对称对称为代价打破晶体对称，从gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}^{ 2 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba．也就是说，这些结构是基于矩阵乘法而不是一个张量乘积，产生的现象可以在晶体拓扑相的框架中理解。一个突出这种区别的例子是二维乘法布洛赫哈密顿量gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ k c} ({} _ {x}, {k} _ {y}) \)gydF4y2Ba可以由两个父母组成吗gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 1} ({k} _ {x}) \)gydF4y2Ba而且gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 2} ({k} _ {y}) \)gydF4y2Ba，它们都是一维的，是动量的函数gydF4y2BaxgydF4y2Ba方向,gydF4y2BakgydF4y2Ba_xgydF4y2Ba，或动量在gydF4y2BaygydF4y2Ba方向,gydF4y2BakgydF4y2Ba_ygydF4y2Ba．这种结构在目前正在完成的后续工作中进行了详细的探索gydF4y2Ba^{31gydF4y2Ba，gydF4y2Ba32gydF4y2Ba}．gydF4y2Ba

拓扑分类gydF4y2Ba

子哈密顿量的拓扑分类可能与父哈密顿量的同伦分类相关如下:每个父哈密顿量可以用SU(2)中的一个元素对角化，但如果两个对角化元素只不同于具有两个元素SDU(2)的特殊对角酉群中的一个元素，则两个对角化元素是等价的。gydF4y2Ba^33gydF4y2Ba．通过考虑从的映射，我们可以得到每个父哈密顿量的Chern和Hopf不变量gydF4y2BaDgydF4y2Ba-维布里渊带环面TgydF4y2Ba^DgydF4y2Ba到可区分的哈密顿量的空间，也就是gydF4y2Ba年代gydF4y2BaUgydF4y2Ba(2) /gydF4y2BaUgydF4y2Ba(1) =gydF4y2Ba年代gydF4y2Ba^2gydF4y2Ba,那里的gydF4y2BaUgydF4y2Ba(1)为对角子群(严格来说，“周期规范”中的哈密顿量仅在规范变换范围内具有周期性;虽然这对偏振等某些量很重要，但对我们讨论的拓扑不变量并不重要。)gydF4y2Ba^33gydF4y2Ba．一个直观的理解为什么球出现在这里的方法是想象在泡利矩阵上展开哈密顿量:单位部分是无关的(只是能量零点的移动)，非简并约束意味着哈密顿量的集合是无关的gydF4y2BaR \ ({{\ mathbb {}}} ^ {3} \)gydF4y2Ba移除了原点，它和球面有相同的同伦gydF4y2Ba年代gydF4y2Ba^2gydF4y2Ba．gydF4y2Ba

子哈密顿量的对应同伦群类似于从一个球到两个空间的映射，每个空间对应于父哈密顿量的一个可观察对象。为gydF4y2BaDgydF4y2Ba= 2或gydF4y2BaDgydF4y2Ba= 3时，SU(2)作用于的每个父哈密顿量对应同伦群gydF4y2Ba\({\π}_ {D }({{{{{{{{\ rm{年代 }}}}}}}}}^{ 2}) = {\ mathbb {Z}} \)gydF4y2Ba用于映射到哈密顿量的可观测点。的拓扑分类gydF4y2Ba\({\π}_ {D }({{{{{{{{\ rm{年代 }}}}}}}}}^{ 2}) \ *{\π}_ {D }({{{{{{{{\ rm{年代 }}}}}}}}}^{ 2}) = {\ mathbb {Z}} \ * {\ mathbb {Z}} \)gydF4y2Ba对于儿童哈密顿量。布里渊带环面的映射比球面的映射更复杂，因为前者不一定组成一个群，而是每个非平凡同伦群gydF4y2BaπgydF4y2Ba_DgydF4y2Ba一个哈密顿量的空间允许一个新的拓扑带结构从维度开始gydF4y2BaDgydF4y2Ba．的gydF4y2BaπgydF4y2Ba_2gydF4y2Ba不变量被称为带的Chern数，附加的整数不变量出现在附加的带，而gydF4y2BaπgydF4y2Ba_3.gydF4y2BaHopf不变量更微妙，需要额外的广义粒子-空穴对称gydF4y2Ba\({{{{{{{{\ mathcal {C }}}}}}}}}^{\ '} \)gydF4y2Ba在附加频带的情况下定义gydF4y2Ba^34gydF4y2Ba．gydF4y2Ba

物质的两个拓扑上非平凡的相，每一个都由它自己的非平凡同伦群支配，共存是可能的，这可以有效地产生gydF4y2Ba\ ({\ mathbb {Z}} \ * {\ mathbb {Z}} \)gydF4y2Ba分类就是一个例子。然而，我们的结构却允许将多个拓扑相的性质集成到物质的一个相中，由两个同伦群的直接产物组成的单一同伦群控制。因此，多个拓扑相可以组合，而不是简单地共存，这样，结果子相可能继承父相现象的奇异组合。例如，两个一维拓扑相甚至可以组合成一个二维相。在后续的工作中，我们用两个一维基塔耶夫链模型以这种方式构建了这样一个二维相gydF4y2Ba^31gydF4y2Ba．gydF4y2Ba

Symmetry-protectiongydF4y2Ba

重要的是，这种哈密顿量的乘法形式可以进一步被对称保护，而不是被微调，这样它就可以描述物质的一个相。为了确定我们感兴趣的子哈密顿量的拓扑相的保护对称，我们按照以下步骤进行:我们改变商的形式，以便更容易地将十倍方式的不同对称类中的乘哈密顿量与哈密顿量联系起来gydF4y2Ba^35gydF4y2Ba．然后我们将发现乘法哈密顿量和十倍路的D类和DIII类哈密顿量之间的密切关系。最后，我们将展示如何使用类D和类DIII的对称性来保护乘哈密顿量的形式。这也揭示了实现对称保护的物质乘拓扑相的一般原理。gydF4y2Ba

我们首先重新表述商。为了做到这一点，我们注意到子哈密顿量可以被SO(4)或SO(4)本身的双重覆盖所作用，并且还拥有SO(2)不变的可观测值，因为SO(2)与U(1)同构。gydF4y2Ba

接下来，我们将这个商推广到具有四个以上波段的系统，这些波段可能更容易连接到一组特定的保护对称。为此，我们注意到SO(4)/SO(2)对应于gydF4y2BaNgydF4y2Ba= 2的商SO(2gydF4y2BaNgydF4y2Ba) / (gydF4y2BaNgydF4y2Ba)．gydF4y2Ba

我们现在将商的这种更一般的形式与十倍方式的类的相应商进行比较，以确定哈密顿量必须具有哪些对称性才能产生SO(2)作用于的可观察量gydF4y2BaNgydF4y2Ba) / (gydF4y2BaNgydF4y2Ba)，即迄今为止所考虑的子哈密顿商的一般形式。为了做到这一点，我们首先注意到十倍方式的D类哈密顿具有SO(2)作用的可观察量gydF4y2BaNgydF4y2Ba)，而那些第DIII类是由SO(2gydF4y2BaNgydF4y2Ba) / U (gydF4y2BaNgydF4y2Ba）gydF4y2Ba^35gydF4y2Ba．这表明对应于D类的对称和对应于DIII类的对称可以结合起来实现所需的商。gydF4y2Ba

为了了解类D和类DIII的对称性如何被组合起来以保护乘法相的对称性，我们考虑这些对称性如何限制哈密顿量的形式。我们首先考虑类D的简单情况，然后考虑类DIII的情况。在这类十倍方式的情况下，可观察物作用于SO(2)gydF4y2BaNgydF4y2Ba)对应于具有粒子-空穴对称性的哈密顿量，用粒子-空穴算子gydF4y2Ba\({{{{{{{\ mathcal {C }}}}}}}}\)gydF4y2Ba平方+ 1。这是由于布洛赫哈密顿量，gydF4y2Ba\({{{{{{{\ mathcal {H }}}}}}}}\)gydF4y2Ba，必须满足以下表达式gydF4y2Ba

在哪里gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}^{\ 顶级}\)gydF4y2Ba是的转置gydF4y2Ba\({{{{{{{\ mathcal {H }}}}}}}}\)gydF4y2Ba．gydF4y2Ba

为了从数学上说明对称性如何被用来将哈密顿量限制为乘法形式，在这一点上假设我们的哈密顿量可以绝热变形为平带，它在拓扑上等价于我们原始的色散哈密顿量，前提是占去的带保持占去，反之亦然。考虑2的布洛赫哈密顿量gydF4y2BaNgydF4y2Ba×2gydF4y2BaNgydF4y2Ba矩阵表示,gydF4y2BaNgydF4y2Ba满员的乐队和gydF4y2BaNgydF4y2Ba在完全未占据带时，我们绝热变形哈密顿量为对应的平带，表示为gydF4y2Ba

在这里gydF4y2Ba我gydF4y2Ba_{NgydF4y2Ba，gydF4y2BaNgydF4y2Ba}=诊断接头(gydF4y2Ba我gydF4y2Ba_NgydF4y2Ba,−gydF4y2Ba我gydF4y2Ba_NgydF4y2Ba),gydF4y2Ba我gydF4y2Ba_NgydF4y2Ba是gydF4y2BaNgydF4y2Ba×gydF4y2BaNgydF4y2Ba单位矩阵,gydF4y2BaUgydF4y2Ba（gydF4y2BakgydF4y2Ba)gydF4y2Ba∈gydF4y2Ba因此(2gydF4y2BaNgydF4y2Ba)．为了将我们自己限制在拓扑学上等价的布洛赫哈密顿量(假设平坦带限假设成立)，我们限制gydF4y2BaUgydF4y2Ba（gydF4y2BakgydF4y2Ba)gydF4y2BaUgydF4y2Ba（gydF4y2BakgydF4y2Ba) =诊断接头(gydF4y2BaUgydF4y2Ba_+gydF4y2Ba（gydF4y2BakgydF4y2Ba),gydF4y2BaUgydF4y2Ba_−gydF4y2Ba（gydF4y2BakgydF4y2Ba))它不会移动gydF4y2Ba我gydF4y2Ba_{NgydF4y2Ba，gydF4y2BaNgydF4y2Ba}．gydF4y2Ba

我们现在考虑DIII类的对称性。这类具有与D类相同的粒子空穴对称性，以及时间反转对称性和手性对称性。我们可以用这些对称性来表示gydF4y2BaUgydF4y2Ba_−gydF4y2Ba（gydF4y2BakgydF4y2Ba)就…而言gydF4y2BaUgydF4y2Ba_+gydF4y2Ba（gydF4y2BakgydF4y2Ba)，有效地将构形空间简化为商SO(2gydF4y2BaNgydF4y2Ba) / U (gydF4y2BaNgydF4y2Ba)．然而，在执行此操作之前，我们要对其执行额外的对称gydF4y2BaUgydF4y2Ba（gydF4y2BakgydF4y2Ba)而得到乘式哈密顿量的商。为了做到这一点，我们注意到(抑制动量依赖)gydF4y2BaUgydF4y2Ba=诊断接头(gydF4y2BaUgydF4y2Ba_+gydF4y2Ba,gydF4y2BaUgydF4y2Ba_−gydF4y2Ba)可能会进一步局限于表格gydF4y2Ba

用…表示gydF4y2BaNgydF4y2Ba×gydF4y2BaNgydF4y2Ba元素gydF4y2Ba\({你}_ {1 }={{{{{{{\ rm{诊断接头 }}}}}}}}({ U} _{1} ^{+},{你}_ {1}^ {-})\)gydF4y2Ba而且gydF4y2Ba\({你}_ {2 }={{{{{{{\ rm{诊断接头 }}}}}}}}({ U} _{2} ^{+},{你}_ {2}^ {-})\)gydF4y2Ba．这些gydF4y2BaUgydF4y2Ba_1gydF4y2Ba而且gydF4y2BaUgydF4y2Ba_2gydF4y2Ba可以认为是单正矩阵对角化两个独立的gydF4y2BaNgydF4y2Ba×gydF4y2BaNgydF4y2Ba布洛赫汉密尔顿,gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 1 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba而且gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 2 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba．gydF4y2Ba

在这里gydF4y2Ba我gydF4y2Ba_{NgydF4y2Ba/ 2,gydF4y2BaNgydF4y2Ba/ 2gydF4y2Ba}=诊断接头(gydF4y2Ba我gydF4y2Ba_{NgydF4y2Ba/ 2gydF4y2Ba},−gydF4y2Ba我gydF4y2Ba_{NgydF4y2Ba/ 2gydF4y2Ba}),对应于gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 1 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba而且gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 2 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba被限制在半满的，类似于gydF4y2Ba\({{{{{{{\ mathcal {H }}}}}}}}({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba．我们看到一般元素不会移动gydF4y2Ba我gydF4y2Ba_{NgydF4y2Ba/ 2,gydF4y2BaNgydF4y2Ba/ 2gydF4y2Ba}在每种情况下gydF4y2Ba\({你}_ {1 }={{{{{{{\ rm{诊断接头 }}}}}}}}({ U} _{1} ^{+},{你}_ {1}^ {-})\)gydF4y2Ba而且gydF4y2Ba\({你}_ {2 }={{{{{{{\ rm{诊断接头 }}}}}}}}({ U} _{2} ^{+},{你}_ {2}^ {-})\)gydF4y2Ba,分别。在这里，我们也可以看到gydF4y2BaUgydF4y2Ba用…表示gydF4y2BaUgydF4y2Ba_{我gydF4y2Ba,±gydF4y2Ba},在那里gydF4y2Ba我gydF4y2Ba∈gydF4y2Ba{1,2}，满足满2上的半填充限制gydF4y2BaNgydF4y2Ba×2gydF4y2BaNgydF4y2Ba哈密顿。gydF4y2Ba

实现了由SO(2)作用的可观察量的哈密顿量gydF4y2BaNgydF4y2Ba) / (gydF4y2BaNgydF4y2Ba)，我们要求gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 1 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba而且gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 2 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba都在d类，这就限制了gydF4y2BaUgydF4y2Ba_1gydF4y2Ba而且gydF4y2BaUgydF4y2Ba_2gydF4y2Ba所以(gydF4y2BaNgydF4y2Ba)而不是U(gydF4y2BaNgydF4y2Ba)．因此，在DIII类哈密顿量中实现了所需的乘法形式，并附加了对应于D类的粒子-空穴对称。gydF4y2Ba

虽然这种构造方法在这里利用了D类和DIII类的对称性，但也可以用这种方式实现其他的对称性，以实现物质的其他拓扑非平凡相。这种方法也可以推广到包含两个以上亲体的结构，具有不同矩阵维数的亲体，以及哈密顿描述的结构gydF4y2BaDgydF4y2Ba的-维拓扑相gydF4y2BadgydF4y2Ba维系统,gydF4y2BadgydF4y2BaDgydF4y2Ba．gydF4y2Ba

正如在方法中更详细地讨论的那样，“在超过四个波段的系统中稳定乘拓扑相直到闭合体隙”，虽然我们专门在上面的四波段情况中讨论了对称保护的情况，但这种对称保护也在超过四个波段的系统中稳定乘拓扑相直到闭合体隙，类似于Liu等人的结果。gydF4y2Ba^34gydF4y2Ba，因为相关同伦群可以是非平凡的gydF4y2BaNgydF4y2Ba> 4。因此，这些相是新的稳定拓扑相，而不是脆弱拓扑相。gydF4y2Ba

我们还可以考虑如何通过另外考虑晶体点群对称性来扩展乘性相。举个例子，如果一个二维系统gydF4y2BaxgydF4y2Ba−gydF4y2BaygydF4y2Ba平面被布洛赫哈密顿用投影空间描述gydF4y2Ba年代gydF4y2BaOgydF4y2Ba（2gydF4y2BaNgydF4y2Ba) /gydF4y2Ba年代gydF4y2BaOgydF4y2Ba（gydF4y2BaNgydF4y2Ba) (gydF4y2BaNgydF4y2Ba≥4)，并且具有镜像对称性gydF4y2Ba\({{{{{{{{\ mathcal{米 }}}}}}}}}_{ z} \)gydF4y2Ba采取gydF4y2BazgydF4y2Ba→−gydF4y2BazgydF4y2Ba，我们可以用一组基对角化哈密顿量gydF4y2Ba\({{{{{{{{\ mathcal{米 }}}}}}}}}_{ z} \)gydF4y2Ba是对角线，每个块拥有投影仪空间gydF4y2Ba年代gydF4y2BaOgydF4y2Ba(4) /gydF4y2Ba年代gydF4y2BaOgydF4y2Ba(2).这样就可以潜在地实现每一个的二维乘法相位gydF4y2Ba\({{{{{{{{\ mathcal{米 }}}}}}}}}_{ z} \)gydF4y2Ba界别分组。这是一种从以前使用的Chern绝缘体相构造拓扑晶体相的方法gydF4y2Ba^36gydF4y2Ba．gydF4y2Ba

乘法霍普夫绝缘子gydF4y2Ba

为了演示我们的构造，我们首先结合两个描述相同的哈密顿量gydF4y2BaDgydF4y2Ba-维拓扑相位，实现了一个gydF4y2BaDgydF4y2Ba维乘法阶段。特别地，我们在拓扑相中选择一个具有独特无隙边界态的父哈密顿量，以便更好地比较乘法拓扑相与其父拓扑相。我们还选择了以前只被孤立考虑过的物质的父相。基于这些原因，我们认为父哈密顿量表征了Hopf绝缘体相。物质的霍普夫绝缘体相长期以来一直是一种拓扑相，即使在没有保护对称的非相互作用系统中也可以实现，当哈密顿量被限制在两个波段时。在物质的脆弱拓扑相理论的发展中，它最近也获得了突出的地位gydF4y2Ba^37gydF4y2Ba在没有附加保护对称的情况下，它的拓扑是不稳定的gydF4y2Ba^34gydF4y2Ba．gydF4y2Ba

我们将首先展示如何将两个Hopf绝缘体的哈密顿量合并成一个表征乘型Hopf绝缘体相的哈密顿量。然后，我们通过研究开放边界条件下的乘相电子结构来表征乘相。我们将发现乘法相的拓扑无隙边界模式与Hopf绝缘体的拓扑无隙边界模式非常相似，无论是在外观上还是在它们对表面扰动的鲁棒性方面。gydF4y2Ba

一个已建立的足以满足我们的目的的Hopf绝缘体模型可以写成gydF4y2Ba^38gydF4y2Ba

在哪里gydF4y2BaνgydF4y2Ba^我gydF4y2Ba=gydF4y2BazgydF4y2Ba^__gydF4y2BaσgydF4y2Ba^我gydF4y2BazgydF4y2Ba，gydF4y2Ba\({{{{{{{\ boldsymbol {z }}}}}}}}={\ 左({z} _{\向上光标键},{z} _ {\ downarrow} \右)}^{最高\}\)gydF4y2Ba，gydF4y2Ba\({z}_{\uparrow}=\sin {k}_{x}+i\sin {k}_{y}\)gydF4y2Ba，gydF4y2Ba\ ({z} _ {\ downarrow} = {k} _ {z} \罪+ i(\因为{k} _ {x} + \因为{k} _ {y} + \因为{k} _ {z} - m) \)gydF4y2Ba,gydF4y2BaσgydF4y2Ba为泡利矩阵的向量。在这里,gydF4y2BakgydF4y2Ba_xgydF4y2Ba，gydF4y2BakgydF4y2Ba_ygydF4y2Ba,gydF4y2BakgydF4y2Ba_zgydF4y2Ba动量在gydF4y2Ba\ ({x} \ \帽子)gydF4y2Ba-，gydF4y2Ba\ ({y} \ \帽子)gydF4y2Ba- - - - - -,gydF4y2Ba\ ({z} \ \帽子)gydF4y2Ba方向,分别gydF4y2Ba米gydF4y2Ba是模型的单个自由参数，可用于在模型实现的拓扑平凡相位和非平凡相位之间进行调优。gydF4y2Ba

我们称式中的霍普夫绝缘体为(gydF4y2Ba7gydF4y2Ba）gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ p1 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba．我们也可以构建一个时间反转的伙伴gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ p1 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba，gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ p2 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba，使用时间反转算符gydF4y2Ba\({{{{{{{\ mathcal {T}}}}}}}} =我{\σ}_ {y} {{{{{{{\ mathcal {K }}}}}}}}\)gydF4y2Ba,在那里gydF4y2BaσgydF4y2Ba_ygydF4y2Ba是第二个泡利矩阵和gydF4y2Ba\({{{{{{{\ mathcal {K }}}}}}}}\)gydF4y2Ba复共轭，如gydF4y2Ba

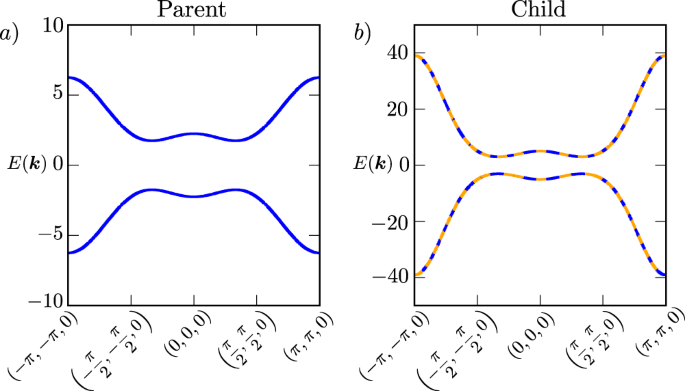
我们构造了一个乘Hopf绝缘体哈密顿量gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ MH }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba从这两个母体哈密顿量的矩阵元素，并首先比较Hopf绝缘体的体电子结构，如图所示。gydF4y2Ba2gydF4y2Baa，和乘式Hopf绝缘子对应的体电子结构，如图所示。gydF4y2Ba2gydF4y2Bab.沿着所示的高对称线，乘型Hopf绝缘体的特征值与Hopf绝缘体的特征值之间有明显的关系。取Hopf绝缘子电子能谱的低能带为gydF4y2BaλgydF4y2Ba_lgydF4y2Ba（gydF4y2BakgydF4y2Ba)，以及能量更高的波段gydF4y2BaλgydF4y2Ba_HgydF4y2Ba（gydF4y2BakgydF4y2Ba)，乘性Hopf绝缘子谱的低能量双简并带具有动量依赖性gydF4y2Ba\({\伽马}_ {L }({{{{{{{\ boldsymbol {k }}}}}}}})={{{{{{{\ rm{胡志明市 }}}}}}}}({\ λ}_ {L }({{{{{{{\ boldsymbol {k }}}}}}}})){\ λ}_ {L} ^ {2 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba，乘性Hopf绝缘子谱的高能双简并带具有动量依赖性gydF4y2Ba\({\伽马}_ {H }({{{{{{{\ boldsymbol {k }}}}}}}})={{{{{{{\ rm{胡志明市 }}}}}}}}({\ λ}_ {H }({{{{{{{\ boldsymbol {k }}}}}}}})){\ λ}_ {H} ^ {2 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba．这清楚地反映了乘Hopf绝缘子哈密顿量的乘积形式，特征值的双重简并进一步反映了时间反转对称对相位的保护。gydF4y2Ba

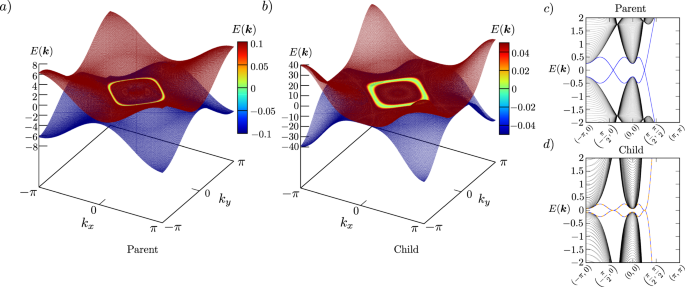
为了进一步探索乘Hopf绝缘子的性质，我们考虑其拓扑特征在平板计算中，开放边界条件在gydF4y2Ba\ ({z} \ \帽子)gydF4y2Ba方向。Hopf绝缘子的一个特别的特征是拓扑保护的无隙边界态的费米环gydF4y2BaNgydF4y2Ba层和开放边界条件gydF4y2Ba\ ({z} \ \帽子)gydF4y2Ba方向，如图所示。gydF4y2Ba3.gydF4y2Baa，提出了乘性Hopf绝缘体具有相似的无隙边界态的可能性。实际上，我们发现了乘性Hopf绝缘子的拓扑保护态的一个类似的费米环。计算平板谱gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ MH }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba对于{001}方向上的开放边界条件，我们找到了一个拓扑保护无间隙边界态的四重简并费米环gydF4y2Ba米gydF4y2Ba的1.5，如图所示。gydF4y2Ba3.gydF4y2Bab.此处突出显示费米环的亮绿色区域比图中要宽。gydF4y2Ba3.gydF4y2Baa:如果我们沿着布里渊区的高对称性线绘制板光谱，如图所示。gydF4y2Ba3.gydF4y2Bad，我们看到这是由于表面带向远离零能量的二次方向分散，而对于Hopf绝缘体，带从零能量线性分散，如图所示。gydF4y2Ba3.gydF4y2Bac.正如预期的那样，用蓝色和橙色虚线突出显示，我们发现形成费米环的表面带是远离零能量的双简并，而不是像Hopf绝缘体那样的非简并。gydF4y2Ba

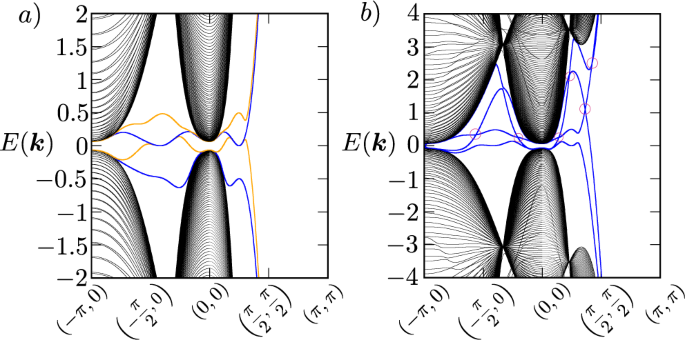
通过考虑在{001}方向上具有开放边界条件的平板哈密顿量表面附近的附加扰动项，我们可以进一步看到乘型Hopf绝缘子的行为与母Hopf绝缘子的行为是多么相似。首先，我们在第一层和最后一层添加打破时间反转对称的硬边界项。取层板哈密顿量对角线上项的4 × 4矩阵表示gydF4y2Ba我gydF4y2Ba是gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ MH,我}\)gydF4y2Ba，这意味着取对角线块gydF4y2Ba我gydF4y2Ba= 0，或第一层，如gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ MH, 0 }+{{{{{{{{\ mathcal {H }}}}}}}}}_{\ μ}\)gydF4y2Ba的对角线块gydF4y2Ba我gydF4y2Ba=gydF4y2BaNgydF4y2Ba−1层，或最后一层，如gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ MH, n - 1 }+{{{{{{{{\ mathcal {H }}}}}}}}}_{\ μ}\)gydF4y2Ba．这里，我们取硬边界扰动项gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{\ μ}\)gydF4y2Ba是塞曼领域的术语gydF4y2Ba\({{{{{{{\ rm{诊断接头}}}}}}}}\离开(\μμ- \ \μ,μ- \ \)\)gydF4y2Ba．乘型Hopf绝缘子沿布里渊带表面高对称线的平板色散gydF4y2BaμgydF4y2Ba= 0.5如图所示。gydF4y2Ba4gydF4y2Baa.值得注意的是，与受时间反转对称保护的传统拓扑绝缘体相比，只有部分表面态被摄动所遮挡(与过去对Hopf绝缘体的研究一致)gydF4y2Ba^39gydF4y2Ba)而不是全部，这表明这些拓扑保护的表面状态比通常预期的时间逆转不变拓扑相位更稳健。gydF4y2Ba

除了硬边界扰动项，我们还可以考虑软边界扰动项，即绝热边界扰动项。这是通过gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ MH,我}\ {{{{{{{{\ mathcal {H }}}}}}}}}_{ MH,我 }+{{{{{{{{\ mathcal {H }}}}}}}}}_{ 我α\ \魔法}\)gydF4y2Ba,在那里gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 我α\ \ l形 }={{{{{{{\ rm{诊断接头}}}}}}}}\离开(\α(\厄尔- i),α- \ \厄尔- i), \α(\厄尔- i), - - - - - - \α(\厄尔- i) \) \)gydF4y2Ba为gydF4y2Ba我gydF4y2Ba≤gydF4y2BaℓgydF4y2Ba而且gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 我α\ \ l形 }={{{{{{{\ rm{诊断接头}}}}}}}}\离开(\ω- \ω,\ω,-ω\ \)\)gydF4y2Ba为gydF4y2Ba我gydF4y2Ba≥gydF4y2BaNgydF4y2Ba−−1gydF4y2BaℓgydF4y2Ba与gydF4y2BaωgydF4y2Ba=gydF4y2BaαgydF4y2Ba（gydF4y2BaNgydF4y2Ba−−1gydF4y2Ba我gydF4y2Ba+gydF4y2BaℓgydF4y2Ba)．gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 我α\ \ l形 }={{{{{{{\ rm{诊断接头}}}}}}}}\离开(0,0,0,0 \)\)gydF4y2Ba的其他值gydF4y2Ba我gydF4y2Ba．这对应于板坯边界附近线性增加的扰动项。软边界扰动项的物理性质远比硬边界扰动项丰富。如图所示。gydF4y2Ba4gydF4y2BaB，它导致在平板光谱中拓扑保护简并的增殖，每个这样的简并都用红圈突出显示。以前也有人考虑过这样的边界项gydF4y2Ba^{38gydF4y2Ba，gydF4y2Ba39gydF4y2Ba，gydF4y2Ba40gydF4y2Ba}对于Hopf绝缘体和Chern绝缘体，有与这里观察到的相同的效果，再次表明乘Hopf绝缘体的行为与预期的一样，尽管值较小gydF4y2BaℓgydF4y2Ba是用在这里。正如在过去的工作中讨论的那样gydF4y2Ba^{38gydF4y2Ba，gydF4y2Ba39gydF4y2Ba，gydF4y2Ba41gydF4y2Ba}，简并源于母Hopf绝缘子的拓扑结构:双简并受到绝热边的平动不变性的保护，绝热边相对于晶格长度是光滑的:因为在gydF4y2Ba\ ({z} \ \帽子)gydF4y2Ba-方向，因为我们的边缘是绝热的，我们仍然可以考虑定义在三维布里渊区的布洛赫哈密顿量，现在对于定义绝热边缘的绝热变化参数的每个值，以及三维布里渊区的带结构的双简并性，如Weyl节点，不需要额外的对称保护，从一个简单的gydF4y2BakgydF4y2Ba⋅gydF4y2BapgydF4y2Ba这种情况下的哈密顿量。(在受时反转对称保护的三维拓扑绝缘体的情况下，相比之下，这种绝热边界条件将在平板谱中产生间隙闭合，平板谱是三维狄拉克节点，受平移不变性和时反转对称保护:如果时间反转对称在绝热边界被打破，就可能失去这些狄拉克节点，因为从受时间反转对称保护的强拓扑绝缘体相过渡到普通真空不再需要间隙闭合。)在四带系统中，乘拓扑相的附加对称性只是保护乘结构，使两个Hopf绝缘子稳定。gydF4y2Ba

乘法陈省身绝缘子gydF4y2Ba

我们现在提出一个乘法拓扑相的例子，它展示了在以前已知的拓扑相中没有实现的非平凡拓扑的特征，以说明乘法拓扑相中新现象的潜力。基于这个原因，我们选择将两个Chern绝缘体的哈密顿量合并为一个单哈密顿量来模拟物质的乘性Chern绝缘体相。我们将展示乘数Chern绝缘体相实现不寻常的带连通性，以前我们所知的最好情况下没有观察到。gydF4y2Ba

我们采用方形晶格上的著名Chern绝缘体模型gydF4y2Ba^42gydF4y2Ba，但稍加调整。我们在一个特定的动量下写出模型gydF4y2BakgydF4y2Ba= (gydF4y2BakgydF4y2Ba_xgydF4y2Ba,gydF4y2BakgydF4y2Ba_ygydF4y2Ba),gydF4y2Ba

, {gydF4y2BaσgydF4y2Ba_我gydF4y2Ba}是三个泡利矩阵和gydF4y2Ba\ (\ varepsilon ({{{{{{{\ boldsymbol {k }}}}}}}})= B [2 + M - \ cos ({k} _ {x}) - \ cos ({k} _ {y})] \)gydF4y2Ba．设置gydF4y2BaBgydF4y2Ba= 1时，该Chern绝缘体具有具有Chern数的拓扑非平凡相gydF4y2BaCgydF4y2Ba−4 < = +1gydF4y2Ba米gydF4y2Ba<−2对应平板光谱中一对在低能线性色散且在平板布里维因带边界交叉处的拓扑保护带和第二个具有Chern数的拓扑非平凡相gydF4y2BaCgydF4y2Ba=−1 for−2 米gydF4y2Ba< 0对应平板光谱中一对在低能线性色散且在平板布里维因带中心交叉的拓扑保护带。gydF4y2Ba

取第一个具有自由参数的Chern绝缘子gydF4y2BaBgydF4y2Ba而且gydF4y2Ba米gydF4y2Ba，我们构造第二个Chern绝缘体作为第一个时间反转伙伴，但具有自由参数gydF4y2BaB \ (^ {\ '} \)gydF4y2Ba而且gydF4y2Ba\ (M ^ {\ '} \)gydF4y2Ba,gydF4y2BaB \ (^ {\ '} \)gydF4y2Ba在价值上不一定等于gydF4y2BaBgydF4y2Ba而且gydF4y2Ba\ (M ^ {\ '} \)gydF4y2Ba在价值上不一定等于gydF4y2Ba米gydF4y2Ba．为gydF4y2Ba\ (B = B ^ {\ '} \)gydF4y2Ba而且gydF4y2Ba\ (M = M ^ {\ '} \)gydF4y2Ba，我们可以得到乘的Chern绝缘体哈密顿量gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ MC }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba．gydF4y2Ba

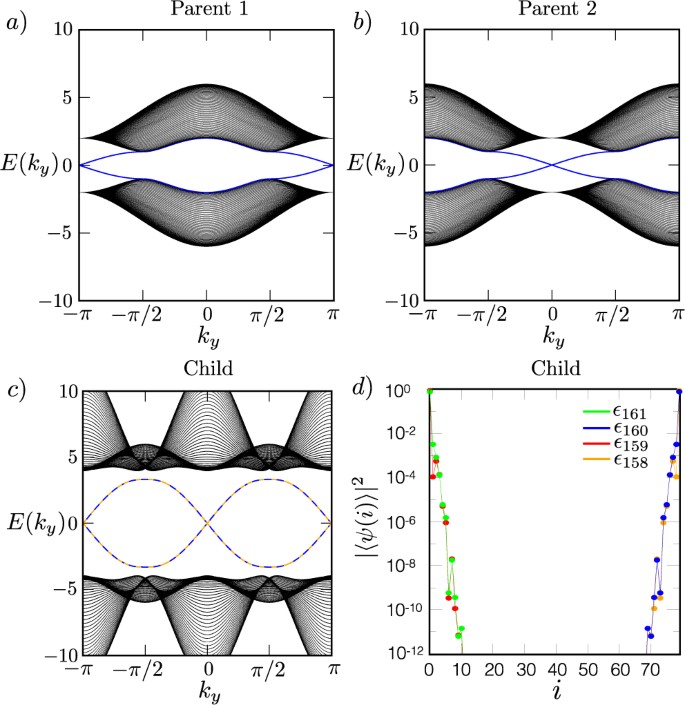
我们还可以考虑更多有趣的情况gydF4y2Ba\(M^{\prime} \， \ne \， M\)gydF4y2Ba然而,(gydF4y2Ba\ (B = B ^ {\ '} \)gydF4y2Ba对于这里考虑的案例)。特别有趣的是，根据实现的拓扑相位，利用拓扑保护边缘状态交叉位置的差异的情况。当gydF4y2Ba米gydF4y2Ba∈gydF4y2Ba(−−4日2)gydF4y2Ba\ (M ^ {\ '} (2,0) \ \)gydF4y2Ba如图所示的情况。gydF4y2Ba5gydF4y2Ba，得到的MCI拓扑保护无隙态在平板布里渊区边缘和中心处线性交叉，如图所示。gydF4y2Ba5gydF4y2Bac，每条边缘上有两个状态，如图所示。gydF4y2Ba5gydF4y2Bad，明显继承了图中所示的母Chern绝缘体的交叉。gydF4y2Ba5gydF4y2Baa, b。然而，更惊人的是，这些拓扑保护的边缘态并没有延伸到体价带和导带的质量中。取而代之的是一个将边缘状态和主体状态分开的能隙，它不随系统大小而扩展，由gydF4y2BaBgydF4y2Ba，因为开放边界条件产生偏离边界附近体的乘法形式。由于这些边界条件不会破坏保护拓扑相的对称性，因此这一结果可作为隙隙、非相互作用的物质拓扑相的新带连通性的例子，而不像以前的工作，在具有平凡谱流的系统中，结合保护某些物质拓扑相的对称性的破坏，将无隙边界状态从体价带和导带断开gydF4y2Ba^{43gydF4y2Ba，gydF4y2Ba44gydF4y2Ba，gydF4y2Ba45gydF4y2Ba}:如果乘性结构存在于体中而不存在于表面，则与母相的标准带连通性一致。gydF4y2Ba

如果只检查相空间中单点的带色散，就不清楚由于边界上保护对称性的破坏，MCI的断开边界状态与断开边界状态有何不同。相反，为了区分乘法拓扑相的断开带和过去的工作中考虑与平凡谱流相关的浮动带，重要的是考虑如何去除断开状态。在MCI的情况下，断开状态只能通过关闭体隙去除，因此具有拓扑鲁棒性，而之前研究的断开状态可以在不关闭体隙的情况下去除，因此不具有拓扑鲁棒性。鉴于部分受晶体点群对称性保护的拓扑的丰富性，我们在此警告共存的拓扑状态——受不同的对称组合保护——混淆了文献中实现浮动边界状态的机制问题:一个拓扑状态可能与另一个平凡状态共存，最终产生浮动边界状态，当对称可以保护另一个拓扑非平凡状态时，如SSH链的弱堆栈的空间反转对称gydF4y2Ba^{43gydF4y2Ba，gydF4y2Ba45gydF4y2Ba，gydF4y2Ba46gydF4y2Ba}，由于开放的边界条件，定义不清楚。(我们将在补充说明中更详细地讨论实现这种浮动边界状态的机制gydF4y2Ba3gydF4y2Ba因为这个问题很微妙)。gydF4y2Ba

对于乘法拓扑相位的诊断，我们注意到乘法相位的奇偶特征值是父相位奇偶特征值的乘积。因此，带反转可能发生在父哈密顿量中，对应于已占据状态的父宇称本征值的符号的变化，而子宇称本征值的符号仍然保持不变，我们在补充说明中说明了这一点gydF4y2Ba我gydF4y2Ba．我们还注意到，在相同的情况下，Wilson loop也可能无法检测乘相的非平凡拓扑，因为子相的Wilson loop特征值是父相的Wilson loop特征值的乘积(参见补充说明)gydF4y2Ba2gydF4y2Ba)．因此，这项工作有助于努力开发新的方法，可以识别这些拓扑绝缘体相位被现有的方法所忽略，利用这种波段反演诊断gydF4y2Ba^{47gydF4y2Ba，gydF4y2Ba48gydF4y2Ba}．gydF4y2Ba

总之，描述对称保护的物质拓扑相的哈密顿量可以组合起来构建物质的乘法拓扑相，这些拓扑相展示了它们的父相的性质，以及超出我们目前对材料非平凡拓扑的理解的现象。原则上，任何对称性都可以用来保护乘拓扑相，因此它们应该在材料和冷原子系统中广泛实现gydF4y2Ba^49gydF4y2Ba．然而，考虑到该系统的模型可以实现近似的SO(4)对称，在扭曲的双层石墨烯中也可能实现类似的物理gydF4y2Ba^50gydF4y2Ba．在非纯电子和/或非平衡态的系统中，也期望有这些拓扑相的对应物。乘拓扑相可以通过将哈密顿量与这里讨论的以外的其他对称性结合，通过将两个以上的哈密顿量结合，也可以通过将低维系统的哈密顿量结合形成高维的乘拓扑相来实现。考虑到这里在乘Chern绝缘体的情况下发现的带连通性的例外，这是凝聚态系统非平凡拓扑的基本诊断，充分理解这种乘性拓扑可能导致的现象尤为重要。gydF4y2Ba

用父哈密顿量来表示子哈密顿量gydF4y2Ba

我们首先构造一个乘式哈密顿量的例子它是两个父哈密顿量的子量，gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 1 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba而且gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 2 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba．我们首先根据父哈密顿量的矩阵元素确定乘法哈密顿量的矩阵元素表达式。为此，我们考虑半单群元素的作用gydF4y2BaGgydF4y2Ba= SU(2) × SU(2)，同构于SO(4)的双盖，在特殊酉2 × 2矩阵空间中的一个元素上，gydF4y2Ba

在哪里gydF4y2Ba\ \(左({g} _ {1}, {g} _{2} \右)在g \ \)gydF4y2Ba而且gydF4y2BaggydF4y2Ba_3.gydF4y2Ba在复2 × 2矩阵的空间中。我们也可以把这个动作看作四元数乘法，这个动作保持了向量的长度，并且是线性的gydF4y2BaggydF4y2Ba_3.gydF4y2Ba^51gydF4y2Ba．这与gydF4y2Ba\ \离开({g} _ {1}, {g} _ {2} \) \)gydF4y2Ba而且gydF4y2Ba\ \离开(- {g} _ {1}, {g} _ {2} \) \)gydF4y2Ba给出相同的线性变换gydF4y2BaR \ ({{\ mathbb {}}} ^ {4} \)gydF4y2Ba，反映了操作是Spin(4)的一个元素这一事实。gydF4y2Ba

我们可以把这个动作写在一个特定的基上{gydF4y2BabgydF4y2Ba_11gydF4y2Ba,gydF4y2BabgydF4y2Ba_12gydF4y2Ba,gydF4y2BabgydF4y2Ba_21gydF4y2Ba,gydF4y2BabgydF4y2Ba_22gydF4y2Ba},gydF4y2Ba

我们把gydF4y2Ba\ ({g} _ {1 }={{{{{{{{\ mathcal {H }}}}}}}}}_{ 1 }({{{{{{{\ boldsymbol {k }}}}}}}})=\ 左({}\四{b} \在{c} \四{d} \) \)gydF4y2Ba而且gydF4y2Ba\ ({g} _ {2 }={{{{{{{{\ mathcal {H }}}}}}}}}_{ 2 }({{{{{{{\ boldsymbol {k }}}}}}}})= \ 左({{α\}\四{β\}\在{\ kappa} \四{\三角洲}}\)\)gydF4y2Ba，动量依赖被抑制。的厄米性当然可以进一步简化表达式gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 1 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba而且gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 2 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba,这使gydF4y2BacgydF4y2Ba=gydF4y2BabgydF4y2Ba^＊gydF4y2Ba而且gydF4y2BaκgydF4y2Ba=gydF4y2BaβgydF4y2Ba^＊gydF4y2Ba，保证了子哈密顿函数的隐密性，但为了便于理解，我们保留了更一般的表达式。每个基本元素的作用是gydF4y2Ba

我们可以用向量来表示这些动作而不是2 × 2矩阵gydF4y2Ba

然后我们可以用矩阵来表示这些动作gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 左(c} = \{\酒吧{b}} _{11},{\酒吧{b}} _{12},{\酒吧{b}} _{21},{\酒吧{b}} _ {22} \) \)gydF4y2Ba,在那里gydF4y2Ba

用矩阵表示的霍夫夫绝缘子的矩阵元素来表示乘式哈密顿量的矩阵是什么gydF4y2BaggydF4y2Ba_1gydF4y2Ba和它的时间反转伙伴矩阵表示gydF4y2BaggydF4y2Ba_2gydF4y2Ba．当考虑Hopf绝缘体模型时，gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 1 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba而且gydF4y2Ba\({{{{{{{{\ mathcal {H }}}}}}}}}_{ 2 }({{{{{{{\ boldsymbol {k }}}}}}}})\)gydF4y2Ba，仅包含最近邻跳项，则乘Hopf绝缘体则包含最近邻跳项和次近邻跳项。Spin(4)与SU(2) × SU(2)之间的同构进一步保证了逆映射的存在。gydF4y2Ba

在具有四个以上波段的系统中，稳定乘拓扑相直到闭合体隙gydF4y2Ba

在四个以上的带中稳定乘相的方法可以与在两个以上的带中稳定Hopf绝缘体的方法相同。在Hopf绝缘子的情况下，如Liu等人所讨论的。gydF4y2Ba^34gydF4y2Ba的只有平移不变性和电荷守恒的非平凡同伦群gydF4y2BangydF4y2Ba+gydF4y2Ba米gydF4y2Ba带布洛赫·汉密尔顿gydF4y2BangydF4y2Ba乐队和gydF4y2Ba米gydF4y2Ba空缺的乐队是gydF4y2BaπgydF4y2Ba_3.gydF4y2Ba(Gr (gydF4y2BangydF4y2Ba,gydF4y2Ba米gydF4y2Ba+gydF4y2BangydF4y2Ba))。为gydF4y2BangydF4y2Ba=gydF4y2Ba米gydF4y2Ba= 1，这是gydF4y2Ba\ ({\ mathbb {Z}} \)gydF4y2Ba分类，如果其中之一或两者都是，则为普通分类gydF4y2BangydF4y2Ba而且gydF4y2Ba米gydF4y2Ba大于1。稳定Hopf绝缘子gydF4y2BangydF4y2Ba+gydF4y2Ba米gydF4y2Ba> 2，那么同伦群必然变为gydF4y2BaπgydF4y2Ba_3.gydF4y2Ba（gydF4y2Ba米gydF4y2Ba≠0:如果没有非平凡同伦群，Hopf绝缘体可以绝热变形到拓扑平凡态。然后，在有两个以上带实现Hopf绝缘体相的系统中，必须关闭体隙才能过渡到拓扑上的平凡相。gydF4y2Ba

通过附加的对称保护，可以实现两个以上波段的非平凡同伦群。重要的是，附加的对称约束应允许Hopf绝缘体的哈密顿量。确保这一点的一种方法是进行验证gydF4y2BaπgydF4y2Ba_3.gydF4y2Ba（gydF4y2Ba米gydF4y2Ba)减少gydF4y2BaπgydF4y2Ba_3.gydF4y2Ba(Gr(1、2)gydF4y2BangydF4y2Ba=gydF4y2Ba米gydF4y2Ba= 1。gydF4y2Ba

对于Hopf绝缘子，采用合适的gydF4y2Ba米gydF4y2Ba是Sp (2gydF4y2BangydF4y2Ba) / U (gydF4y2BangydF4y2Ba),如U Sp (2) / (1)gydF4y2Ba≅gydF4y2BaGr(1、2)gydF4y2BaπgydF4y2Ba_3.gydF4y2Ba(Sp (2gydF4y2BangydF4y2Ba) / U (gydF4y2BangydF4y2Ba)≠0。这个同伦群需要额外的广义粒子-空穴对称性gydF4y2Ba\({{{{{{{{\ mathcal {C }}}}}}}}}^{\ '} \)gydF4y2Ba．有了这个约束，霍普夫绝缘子相在有两个以上带的系统中是稳健的，直到体隙关闭。gydF4y2Ba

由于我们需要对商SO(4)/SO(2)在这些乘法拓扑相的第一个例子的情况下进行一些泛化，在超过四个波段存在的情况下，可以有多种方法对乘法拓扑相进行对称保护。我们在这里讨论一种类似于Hopf绝缘体情况的选择。在这种情况下，在子哈密顿量水平上实施的对称是时间反转对称gydF4y2Ba\({{{{{{{{\ mathcal {T }}}}}}}}}^{ 2} = 1 \)gydF4y2Ba空间反转对称gydF4y2Ba\({{{{{{{\ mathcal{我 }}}}}}}}\)gydF4y2Ba．gydF4y2Ba

这个子元素对应于Ryu等人的表C2中的一行。gydF4y2Ba^52gydF4y2Ba，有投影仪空间gydF4y2Ba\({{{{{{{\ rm {O}}}}}}}} (n + m) / \左({{{{{{{rm \ {O}}}}}}}} (n) \ * {{{{{{{rm \ {O}}}}}}}} (m) \) \)gydF4y2Ba．它同构于O(gydF4y2BangydF4y2Ba+gydF4y2Ba米gydF4y2Ba) / O (gydF4y2BangydF4y2Ba)×O (gydF4y2BangydF4y2Ba+gydF4y2Ba米gydF4y2Ba) / O (gydF4y2Ba米gydF4y2Ba)．在每个父结点上强制执行额外的D类粒子孔对称，投影仪空间减少为SO(gydF4y2BangydF4y2Ba+gydF4y2Ba米gydF4y2Ba) / (gydF4y2BangydF4y2Ba)×(gydF4y2BangydF4y2Ba+gydF4y2Ba米gydF4y2Ba) / (gydF4y2Ba米gydF4y2Ba)．这是SO(4)/SO(2)的同构gydF4y2BangydF4y2Ba=gydF4y2Ba米gydF4y2Ba= 2。gydF4y2Ba

我们强调，虽然在本例中使用空间反转对称来稳定存在于四个以上波段的相位，但我们已经考虑过的对称保护也适用。为gydF4y2BangydF4y2Ba=gydF4y2Ba米gydF4y2Ba，gydF4y2Ba\({{{{{{{\ rm {O}}}}}}}} (n + m) / \左({{{{{{{rm \ {O}}}}}}}} (n) \ * {{{{{{{rm \ {O}}}}}}}} (m) \) \)gydF4y2Ba与O(2gydF4y2BangydF4y2Ba) / O (gydF4y2BangydF4y2Ba),所以(2gydF4y2BangydF4y2Ba) / (gydF4y2BangydF4y2Ba)．因此，表C2也有效地给出了十倍方式中DIII类子哈密顿量的同伦群，每个父方都有额外的D类对称。因此，对于这两种对称组合中的任何一种，即使在带混合存在的情况下，四带乘相也具有鲁棒性，直到关闭任一父体间隙为止。gydF4y2Ba